从 GEMM 到 DeepGEMM：GPU 矩阵计算原理与优化

1. 什么是GEMM？

1.1 GEMM简介

GEMM（General Matrix to Matrix Multiplication，通用矩阵的矩阵乘法）是BLAS（Basic Linear Algebra Subprograms）库中的一个函数，用于实现矩阵与矩阵之间的乘法运算。BLAS库是一组用于执行基础线性代数运算的子程序库，包括向量加法、数乘、点积、矩阵相乘等。

GEMM 的数学原理

GEMM 的基本公式：

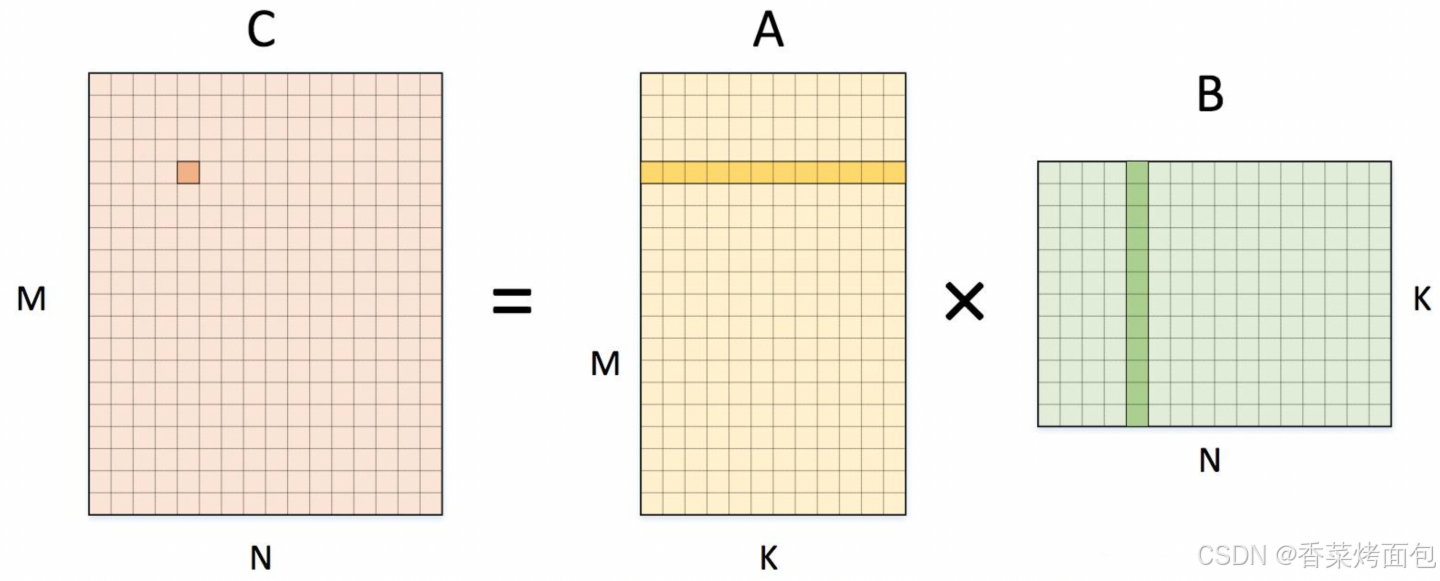
如上图所示，简单来说，GEMM就是将两个矩阵相乘，得到一个输出矩阵的过程。

GEMM 的Naive实现：

for (int m = 0; m < M; m++) {
  for (int n = 0; n < N; n++) {
    C[m][n] = 0;
    for (int k = 0; k < K; k++) {
      C[m][n] += A[m][k] * B[k][n];
    }
  }
}

计算量为 2*M*N*K（其中2为循环最内层的一次乘法和加法）

这个过程在深度学习中非常常见，经常需要进行大量的矩阵运算。深度学习模型通常由多个网络层组成，每个网络层都包含大量的神经元，这些神经元通过权重和偏置进行连接，形成一个庞大的矩阵。在模型训练过程中，需要不断地对这些矩阵进行运算，以调整权重和偏置，使得模型的预测结果更加准确。一些典型的神经网络层，都需要执行数千万次浮点运算（FLOP）‌。

Naive 实现的效率非常低，每次只计算一次，通过分块计算（Tiling） 可以减少内存访问，提高计算效率，并逐步优化访存模式。

计算拆分的核心思想

Step1：拆分 N 维度

将计算划分成更小的块，例如 每次计算 1×4 的小块，即：计算该块输出时，需要使用 A 矩阵的 1 行，和 B 矩阵的 4 列：

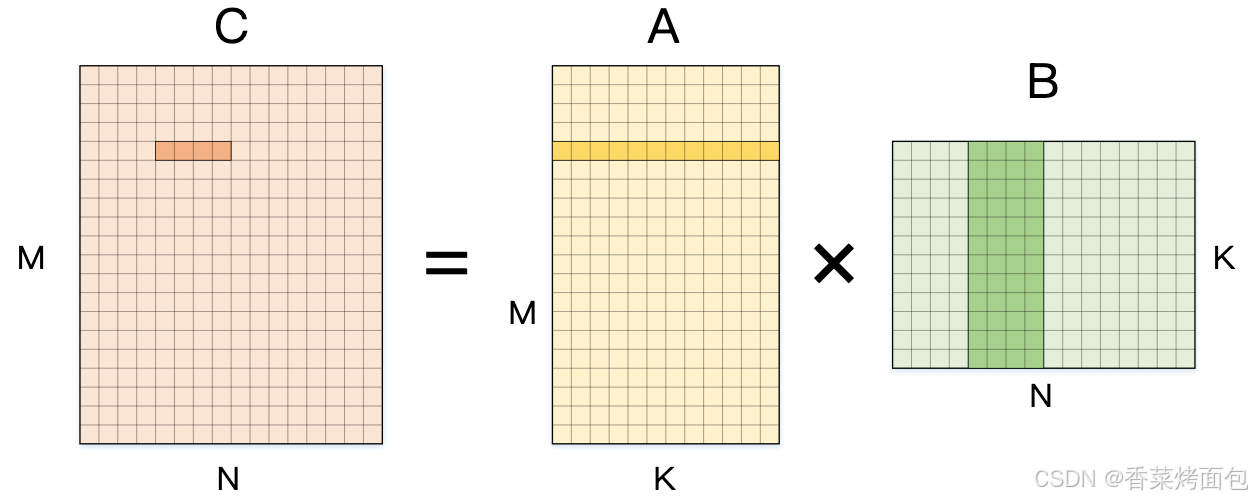
for (int m = 0; m < M; m++) {
  for (int n = 0; n < N; n += 4) { // 一次计算 4 列
    C[m][n + 0] = 0;
    C[m][n + 1] = 0;
    C[m][n + 2] = 0;
    C[m][n + 3] = 0;
    for (int k = 0; k < K; k++) {
      C[m][n + 0] += A[m][k] * B[k][n + 0];
      C[m][n + 1] += A[m][k] * B[k][n + 1];
      C[m][n + 2] += A[m][k] * B[k][n + 2];
      C[m][n + 3] += A[m][k] * B[k][n + 3];
    }
  }
}

上述伪代码的最内侧计算使用的矩阵 A 的元素是不变的，连续使用四次，因此可以将 A[m][k] 读取到内存中，从而实现 4 次数据复用，相较于逐列计算，每次计算 4 列，访存减少

Step2：进一步拆分 M 维度

类似地，再对 输出矩阵的行（M 方向）也进行分块，例如 一次计算 4×4 小块，每次计算 16 个元素：

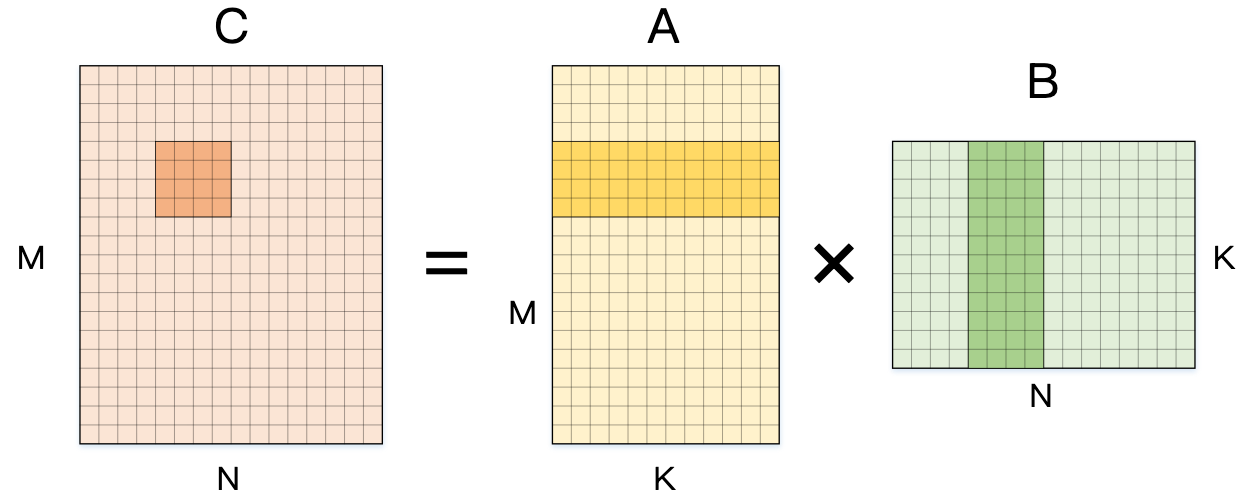
for (int m = 0; m < M; m += 4) { // 一次计算 4 行
  for (int n = 0; n < N; n += 4) { // 一次计算 4 列
    C[m + 0][n + 0..3] = 0;
    C[m + 1][n + 0..3] = 0;
    C[m + 2][n + 0..3] = 0;
    C[m + 3][n + 0..3] = 0;
    for (int k = 0; k < K; k++) {
      C[m + 0][n + 0..3] += A[m + 0][k] * B[k][n + 0..3];
      C[m + 1][n + 0..3] += A[m + 1][k] * B[k][n + 0..3];
      C[m + 2][n + 0..3] += A[m + 2][k] * B[k][n + 0..3];
      C[m + 3][n + 0..3] += A[m + 3][k] * B[k][n + 0..3];
    }
  }
}

访存复用率更高，A[m][k] 复用 4 次，B[k][n] 复用 4 次，进一步减少访存，这些改进都是通过展开循环后利用寄存器存储数据减少访存得到的

• A[m][k] 复用 4 次：在最内层循环中， A[m][k] 在一次 k 迭代中，计算 C[m][n + 0] 到 C[m][n + 3]，即 4 个输出元素
• B[k][n] 复用 4 次：在 for (int m = 0; m < M; m++) 的外循环中，每个 k 迭代， B[k][n + i] 也会被 m 方向的所有计算使用
• n + 0..3 表示对连续 4 个元素的操作，即连续 4 个 n 方向的计算， C[m][n] 在 n 维度上 4 次计算的展开

Step3：拆分 Reduction 维度 K

 

在计算 4×4 输出时，将维度 K 拆分，从而每次最内侧循环计算出输出矩阵 C 的 4/K 部分和：

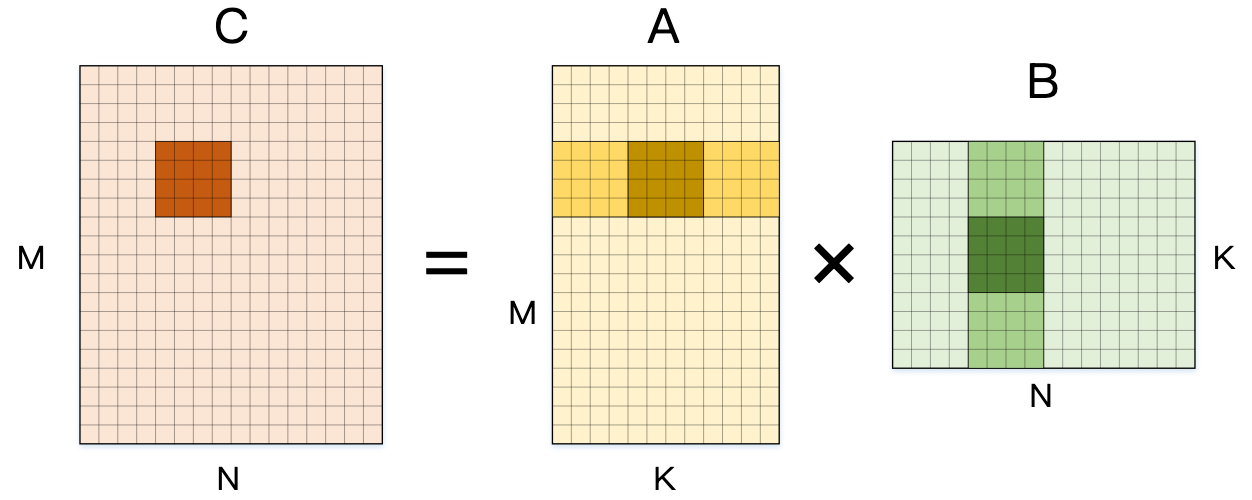
下面展示的是这部分计算的展开伪代码，其中维度 M 和 N 已经被简写，最内侧循环发生的计算次数已经从 Naive 版本的 2（一次乘法和加法） 发展到了 2 × 4 × 4 × 4 =128 。

for (int m = 0; m < M; m += 4) {
  for (int n = 0; n < N; n += 4) {
    C[m + 0..3][n + 0..3] = 0;
    for (int k = 0; k < K; k += 4) { // 一次计算 4 轮 K
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 0] * B[k + 0][n + 0..3];
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 1] * B[k + 1][n + 0..3];
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 2] * B[k + 2][n + 0..3];
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 3] * B[k + 3][n + 0..3];
    }
  }
}

A[m][k] 和 B[k][n] 在 4 轮计算中复用

在对 M 和 N 展开时，可以分别复用 B 和 A 的数据；在对 K 展开时，其局部使用的 C 的内存是一致的，那么在 K 迭代时可以将部分和累加在cache中，进一步减少访存

现代处理器会使用更大的分块（如 8×8、 16×16、32×32），但是一条 MLA （Multiply-Accumulate）指令只能完成一次乘加，结合 SIMD 指令【3.2】，同时对多个数据进行处理可以进一步加速计算，那么进一步优化矩阵乘法，利用向量操作来提高计算性能：

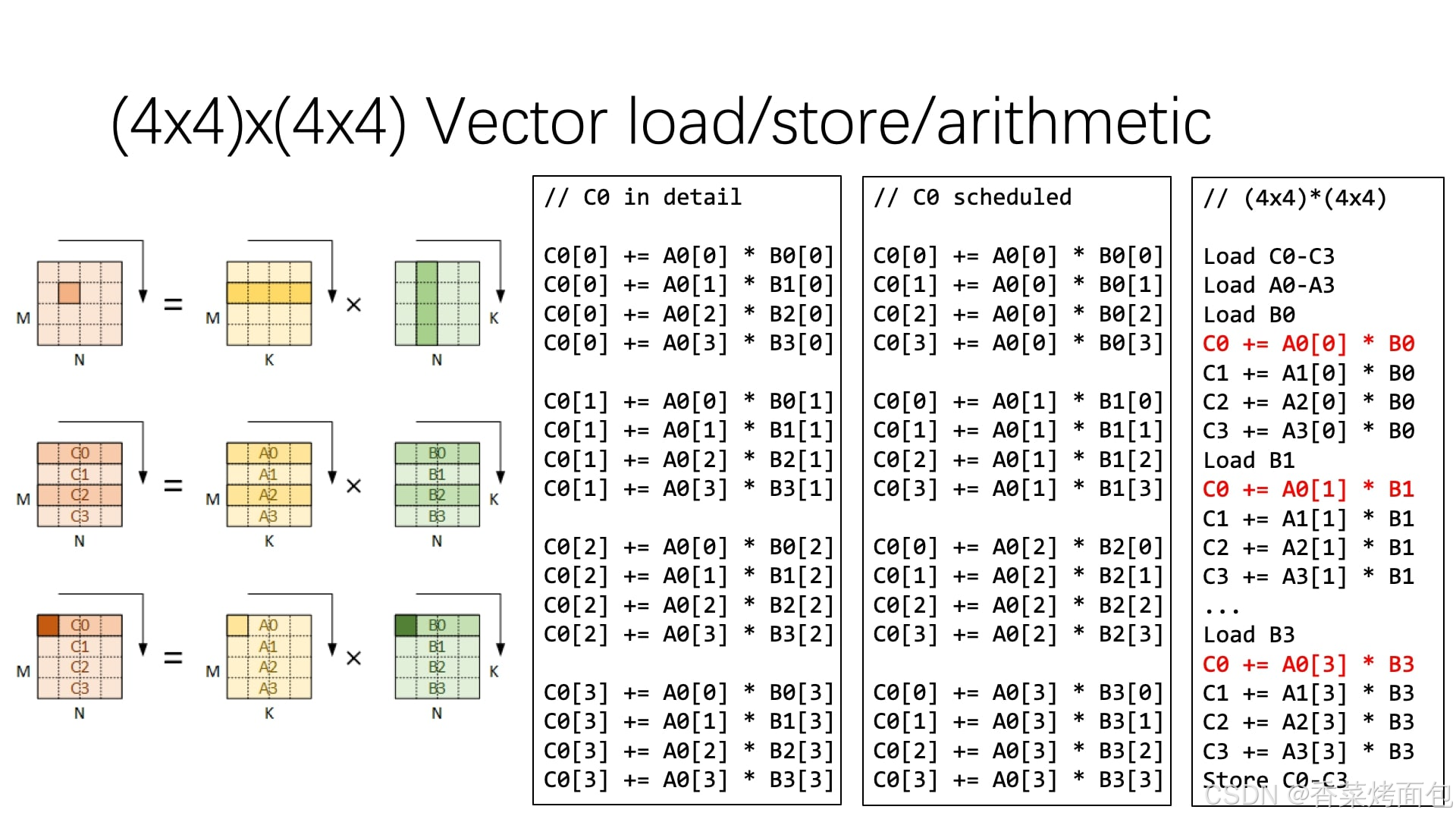
• C0 in detail 直接计算：Naive 展开计算 C0 的方法，每次计算一个元素，但由于访存模式不连续
• C0 scheduled：对计算过程进行重排，先加载 A 的一整行 A0, A1, A2, A3，计算过程中 B0, B1, B2, B3 按列顺序存取，访存更连续
• (4×4)*(4×4)：利用 SIMD 指令 实现 向量化计算
  • A0-A3 是连续存储的，可以 一次性加载，B0, B1, B2, B3 也是按列存储的，每次访问后可复用
  • 原始计算需要 64 条指令，而 SIMD 计算 减少到 16 条指令，在 一条指令内完成 4 个乘加运算
• 这张图体现了矩阵计算优化的 访存优化 和 向量化计算 两大核心思想，在 GPU 计算和高性能计算（HPC）中广泛应用

Load C0-C3      // 载入 C 矩阵
Load A0-A3      // 载入 A 矩阵
Load B0         // 载入 B 矩阵的第一列

C0 += A0 * B0   // 使用 SIMD 指令计算 4 个元素
C1 += A1 * B0
C2 += A2 * B0
C3 += A3 * B0

Load B1         // 载入 B 矩阵的第二列
C0 += A0 * B1   // 继续计算
C1 += A1 * B1
C2 += A2 * B1
C3 += A3 * B1
...
Load B3         // 载入 B 矩阵的最后一列
C0 += A0 * B3
C1 += A1 * B3
C2 += A2 * B3
C3 += A3 * B3

Store C0-C3     // 存储计算结果

以上就是GEMM优化的原理，这类优化是 GEMM（通用矩阵乘法） 实现的核心，广泛用于 GPU 矩阵计算。



小结

总结来看，Naive 实现的效率非常低，主要存在的问题有以下几点：

1️⃣ 循环最内层计算量非常少，循环开销大

• 每次循环的计算量只有一次 乘法+加法， C[m][n] += A[m][k] * B[k][n]
• 每次只计算一个元素，GPU核心利用率极低，访存次数极多（每次都访问A[m][k]和B[k][n]），没有发挥并行计算的优势

⁉️为什么GPU核心利用率低？

• 比如H100 SXM GPU有 18432 个CUDA核心，Naive版本的GEMM，每个线程只计算一个元素，其他核心都是空闲的，导致利用率极差

✅ 解决方法——Tile-based GEMM（块状矩阵乘法）

• 将C矩阵划分成子块，例如：
  • 每个线程（Thread）计算一个 4×4 子矩阵
  • 每个线程块（Thread Block）计算一个 32×32 的子矩阵
• GPU核心利用率提高，访存次数减少，计算密度增加

2️⃣ 对于B矩阵，每次读取B[k][n]时，都有可能触发cache miss缓存缺失

• 在Naive实现中，内存访问模式如下：
  • A矩阵：A[m][k] 是按照 行优先的方式读取，访问模式是 连续的，这对缓存友好
  • B矩阵：B[k][n] 是按照 列优先的方式读取，导致访问模式是非连续的，读取 B[k][n] 都需要跨内存行，非常容易导致缓存缺失，带宽消耗大

✅ 解决方法

• Shared Memory（共享内存）优化
  • GPU有一种超快的缓存，叫共享内存（Shared Memory），可以将B矩阵的子块提前加载到共享内存
• 块矩阵计算（Tiling/Blocking）：将矩阵划分成小块，让A和B的子块都能够完全装入Cache，避免Cache Miss
• 矩阵转置：在计算前将B矩阵进行转置，使B的内存访问变成连续访问



3️⃣ 未利用 Tensor Core

• H100 / A100 / V100等GPU，Tensor Core是核心计算单元，进行块状矩阵乘法速度比CUDA核心快 10倍以上
  • 普通CUDA核心：一次计算1个乘法+加法
  • Tensor Core：一次计算4x4 或 8x8 或 16x16等块状矩阵乘法
• Naive版本的GEMM是逐元素计算，Tensor Core是块级计算（Tile-based）
• 必须用Tile-based GEMM，并使用cutlass库或cuBLAS库才能激活Tensor Core



矩阵计算如何在GPU上加速？除了GEMM本身计算的优化，也与GPU的计算架构有关（SIMT、Warp、Thread Block）

2. GPU计算架构与矩阵计算

2.1 GPU的计算架构

官方文档：Life of a triangle - NVIDIA's logical pipeline | NVIDIA Developer

GPU的诞生

在最开始的时候，GPU（Graphics Processing Unit）的功能与名字一致，是专门用于绘制图像和处理图元数据的特定芯片。在没有GPU的时候，人们想将计算机中的数据显示在屏幕上，是使用CPU来进行相关运算的。我们要做的事情简单概括一下，就是通过对数据进行相应的计算，把数据转换成一个又一个图片上的像素，然后将这张图片显示在屏幕上。整个流程中的计算并不复杂，但是数量大，且计算流程重复，如果全盘交给CPU的话会给其造成很大的性能负担。于是乎GPU诞生了。

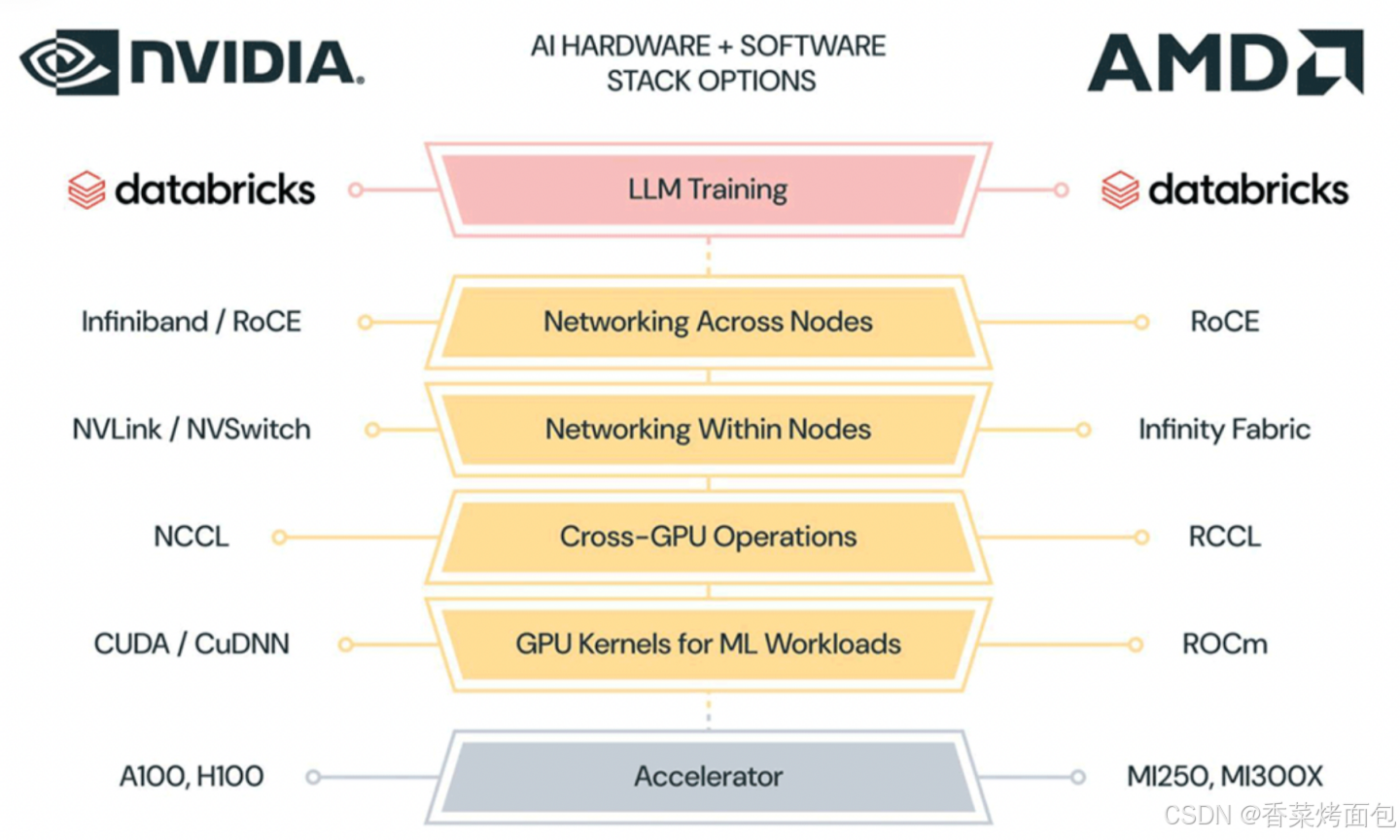
下图分别展示了英伟达和 AMD 的工具链架构，可以看到两者的层次架构都是十分相像的，最核心的区别实则在于中间的 libraries 部分，两家供应商均根据自己的硬件为基础 library 做了优化；此外在编译层面两方也会针对自身架构，在比如调度，算子融合等方面实现各自的编译逻辑。



GPU vs. CPU

下图是GPU与CPU的构成差异图：

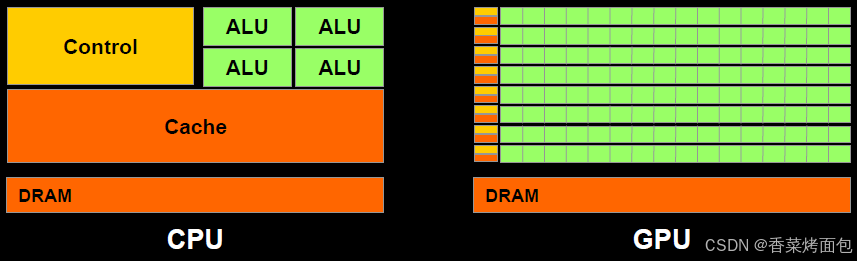
绿色代表的是computational units(可计算单元) 或者称之为 cores(核心)，橙色代表memories（内存），黄色代表的是control units（控制单元）。

总的来看，可以这样说：CPU的计算单元是“大”而“少”的，然而GPU的计算单元是“小”而“多”的

• CPU：拥有少量的计算单元（ALU），更适合处理顺序执行的任务，擅长逻辑控制和串行计算，适合控制密集型场景
• GPU：并行计算加速器，适合大规模数据并行处理，GPU则是以并行处理见长。它拥有成百上千个核心，这些核心被设计成同时处理多个简单的任务，特别适合大规模的数据并行计算

在现代计算中，CPU 与 GPU 常协同工作（如 CPU 负责调度，GPU 负责加速），形成异构计算架构。



GPU 计算架构

GPU架构是围绕一个流式多处理器（SM，Streaming Multiprocessor）的扩展阵列搭建的，通过复制这种结构来实现GPU的硬件并行：

(a) GPU硬件架构——每个SM包含多个Core，所有SM共享L2 Cache，并连接到全局内存（DRAM）

• 整体结构
  • 多个SM 组成整个GPU，L2 Cache 连接所有SM，用于缓存全局内存访问
  • DRAM（全局内存） 是GPU的主存储器，所有SM可以访问，但访问速度较慢
  • Host Interface & Giga Thread：用于管理CPU（Host）和GPU（Device）之间的任务分配
• SM（Streaming Multiprocessor）
  • 每个SM（流式多处理器）内部包含多个Core（核心），即流处理单元（SP，Streaming Processor）
  • SM内部还有共享内存（Shared Memory）/ L1 Cache，用于加速线程间的数据交换
  • 寄存器文件（Register File） ，每个SM都有一组寄存器

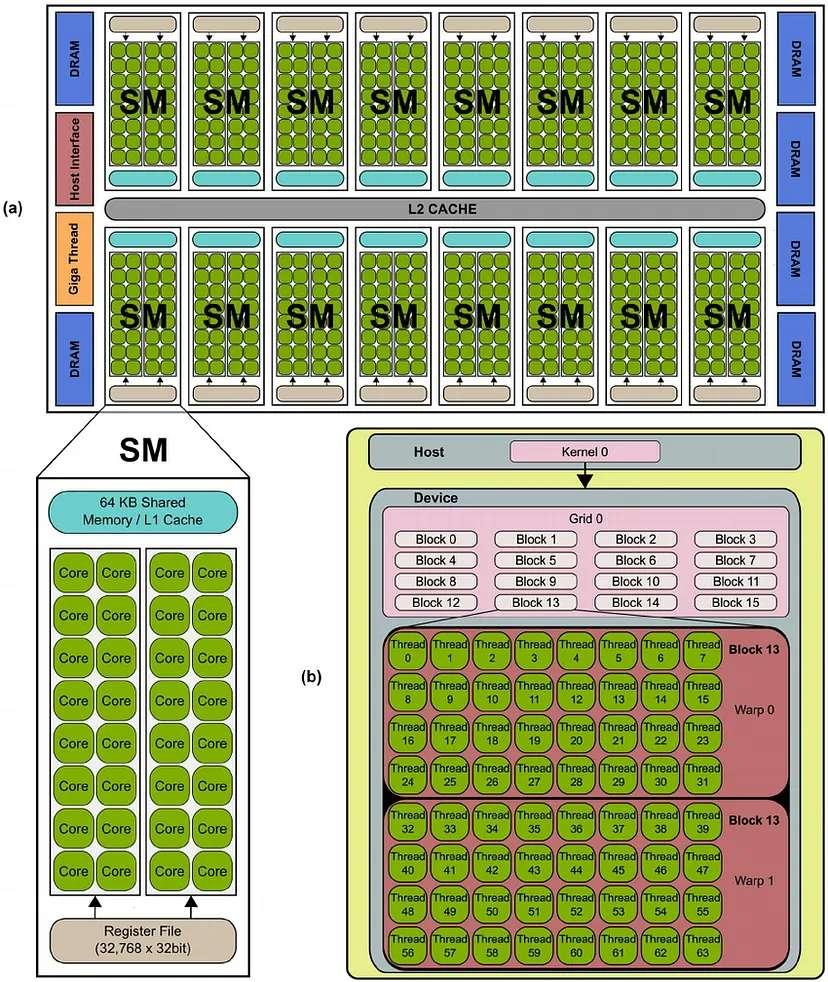
(b) CUDA编程模型——Host 端启动Kernel，Device 端的Grid 由多个Block 组成，每个Block 包含多个Thread，线程以Warp为单位执行

CUDA的层次化线程组织：

• Host（主机端）：CPU（Host）启动Kernel 0（CUDA核函数）
• Device（设备端）
  • GPU被组织为Grid（网格），一个Grid由多个Thread Block（线程块） 组成
  • 线程块的编号从Block 0到Block 15，每个Block会被分配到某个SM执行
• Thread Block 内部结构
  • 每个Block由多个Thread（线程） 组成
  • 线程束（Warp）：线程是以Warp（线程束） 为单位执行的，一个Warp通常包含32个线程。例如，在Block 13中，可以看到Warp 0 和 Warp 1，每个Warp有多个线程（Thread 0, Thread 1, …）



流式多处理器（SM）

流式多处理器（SM）是GPU的基础运算单元，上图可以看出SM关键组件包括：CUDA核心、共享内存/一级缓存、寄存器文件等。

GPU中每个SM都能支持数百个线程并发执行，每个GPU通常有多个SM，每个SM都能独立运行，具备并行处理多个程序的能力。在GPU的整体架构中，SM的数量直接决定了其计算能力的强弱。当一个程序在GPU上运行时，它会被拆解并分配到多个SM上，每个SM负责处理其中一部分数据，SM的数量越多，意味着GPU可以同时处理的数据量越大，程序的运行速度也就越快。

每个 SM 具有 32 个 CUDA 内核（每个架构不一样，H100每个SM有128个CUDA核心，H100 SXM 有144 个SM，H100 PCIe 有114个SM），就是图中写着Core的绿色小方块，每个 CUDA 内核都有一个完全流水线化的整数算术逻辑单元 (ALU) 和浮点单元 (FPU)：

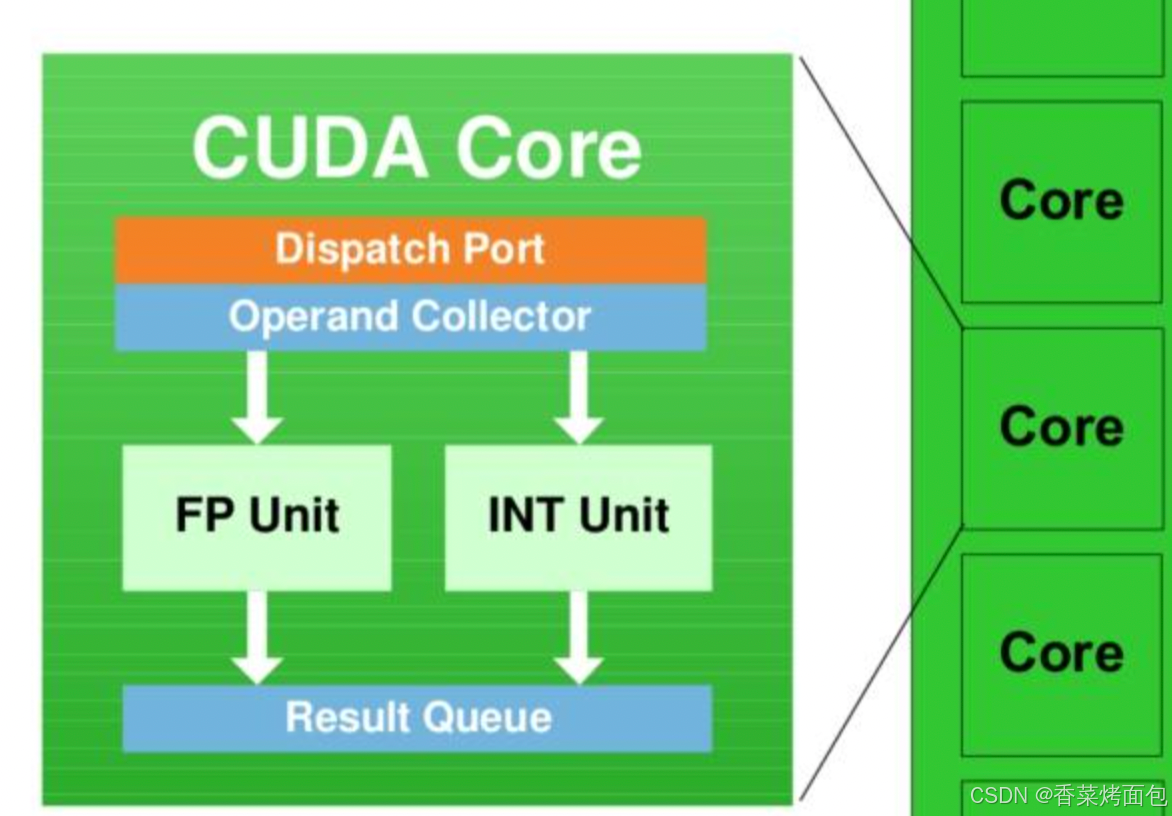
GPU内核

GPU内核是GPU中执行计算操作的最小单元。与CPU内核不同，GPU内核针对浮点运算（FLOPs）进行了专门优化。在每个运算周期内，每个GPU内核都能够执行一次浮点运算操作。这种设计使得GPU在处理涉及大量浮点运算的任务，如深度学习模型训练时，展现出远超CPU的计算优势。

线程束（warp）

为了进一步提升并行计算效率，GPU内核会被分组为线程束（warp）。不同厂商的GPU产品，每个线程束包含的内核数量有所差异。

例如，英伟达（Nvidia）的GPU每个线程束包含32个内核，而AMD的GPU每个线程束则有64个内核。CUDA 采用单指令多线程SIMT架构管理执行线程，在线程束中，所有内核必须同时执行相同的指令，但它们处理的数据各不相同。线程束作为一个整体协同工作，确保所有内核能够同步执行指令。

然而，如果工作负载的数据结构（如张量形状）与线程束大小不匹配（例如，张量形状不是32或64的倍数），那么部分内核就会处于闲置状态，无法参与运算，这种现象被称为线程束发散（warp divergence）。线程束发散会导致GPU资源的浪费，降低计算性能。因此，在设计AI工作负载时，将张量形状设置为32（英伟达GPU）或64（AMD GPU）的倍数，可以确保线程束中的所有内核都能得到充分利用，减少内核闲置情况，从而有效提升GPU的计算性能。

软件抽象

硬件资源：

• SM (Streaming Multiprocessor)：GPU的核心处理单元，每个SM可以同时执行多个线程。每个SM通常包含多个SP，即流处理单元（Streaming Processor）
• SP (Streaming Processor)：实际执行计算的硬件单元，每个线程会被映射到一个SP上执行，SP的数量直接决定了GPU的并行计算能力，每个SP可以看作是一个CUDA Core

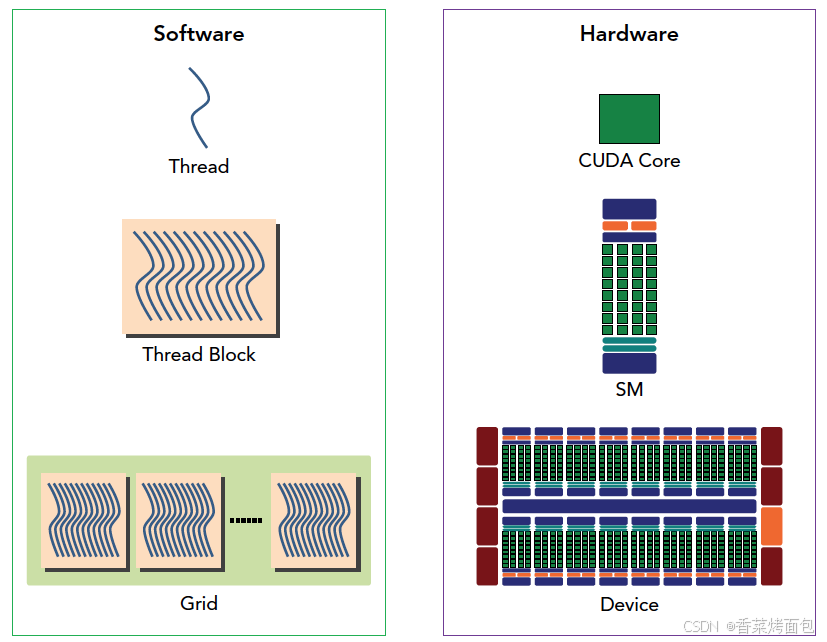
软件抽象：

• Thread (线程)：在CUDA程序中，线程是最基本的执行单元，每个线程执行一个计算任务
• Warp 或 Wavefront (线程束)：线程束是GPU中执行的最小单元，通常包含32个线程。一个线程束中的线程会一起执行相同的指令，但每个线程可以处理不同的数据。由于GPU的硬件设计，32个线程会同时被调度到SP上执行
• Thread Block (线程块)：多个 Warp 组成的一个计算单元，每个线程块会在一个SM上执行，但不同的线程块可能会被分配到不同的SM上。线程块的数量和每个线程块的大小（线程数）可以影响程序的性能
• Grid (线程网格)：多个 Block 形成整个计算任务，整个程序的所有线程都会在一个网格内进行管理和调度

grid、block以及warp关系：——Grid，Block，thread都是线程的组织形式，最小的逻辑单位是一个thread，最小的硬件执行单位是thread warp，若干个thread组成一个block，block被加载到SM上运行，多个block组成一个Grid

Kernel 指的是在GPU上执行的函数，在执行时会以一个grid为整体，划分若干个block，然后将 block 分配给 SM 进行运算。block 中的线程以32个为一组，称为warp，进行分组计算。block会以连续的方式划分warp。

例如，如果一个block由64个thread，则分为2组warp。0-31为warp0，32-63为warp1，如果block不是32的倍数，则多余的thread独立分成一组warp，例如block有65个thread，则最后一个thread单独为一个warp，那么此时这个warp中的其他thread处于非活动状态。



内存层次结构

GPU配备了一套复杂精妙的内存层次体系，目的在于最大程度提升计算效率。GPU中的三种主要内存类型如下：

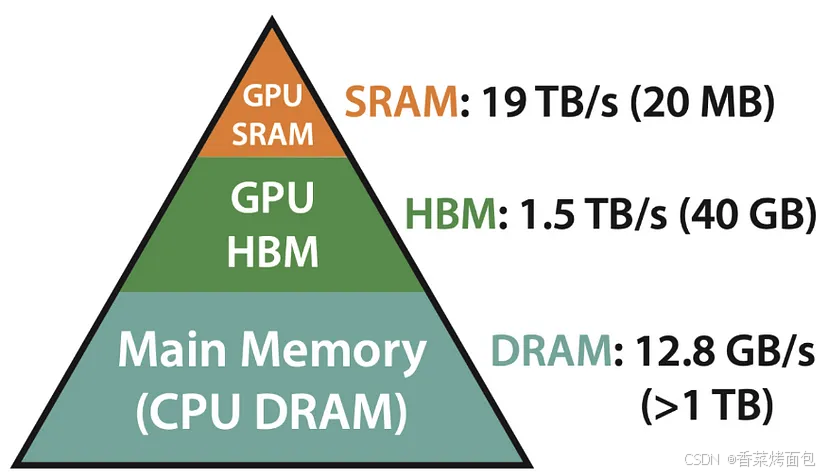
SRAM（静态RAM）——最快的缓存内存

SRAM位于GPU内核内部，整合了寄存器、L1缓存和L2缓存：

• 寄存器：作为每个GPU内核中极为微小却拥有超高速读写速度的内存单元，寄存器用于存储内核正在处理的即时数据，因其直接与内核紧密协作，数据读写几乎零延迟，堪称GPU内存体系中速度最快的部分
• L1缓存：这是流式多处理器（SM）内部的一级缓存，它存储着程序频繁访问的数据，大大加快了计算进程，减少了对速度相对较慢的DRAM等内存的访问次数
• L2缓存：属于更大容量的二级缓存，可供多个SM共享使用。当L1缓存无法容纳某些数据时，L2缓存便能发挥作用，存储并重复利用这些数据，从而降低了GPU对外部内存（VRAM）的依赖程度。

为什么这很重要？ 寄存器、L1和L2缓存能够显著加快GPU的数据处理速度，关键就在于它们减少了从较慢的全局内存（VRAM/DRAM）中读取数据的需求。对于对实时性要求极高的工作负载而言，优化数据在这些缓存中的存储方式，能直接提升GPU的运行性能。它就像是给GPU配备了一个便捷的“数据速取库”，让计算过程更加流畅高效。同时，由于制造成本高昂，SRAM虽然速度极快，但容量相对较小。

DRAM（动态RAM）——主存储器（GPU中的VRAM）

DRAM位于GPU显卡上，作为GPU的视频随机存取存储器（VRAM）发挥作用。它主要用于存储大量数据，像AI模型的权重参数等都存储在这里。DRAM的存储容量比SRAM大得多，但读取速度相对较慢。在实际应用中，GPU通常会使用GDDR（图形DDR）类型的DRAM内存，以满足图形处理和计算任务对数据存储的需求。

HBM（高带宽存储器）——高性能VRAM

HBM主要应用于面向AI和深度学习等高负载需求的高性能GPU中。它采用了独特的垂直堆叠内存技术，这种设计极大地缩短了数据传输路径，有效降低了数据访问延迟，并显著提升了内存带宽。与传统的GDDR内存相比，HBM的速度优势十分明显。不过，由于其技术复杂、成本高昂，目前仅在一些高端、专业的GPU产品中使用。



注意⚠️：GPU显存（VRAM，Video RAM）主要指的是DRAM（动态RAM），具体来说，是GPU上使用的GDDR（图形DDR）或HBM（高带宽存储器）

• GDDR（Graphics DDR） 是大多数消费级和专业级GPU（4090等）使用的显存，具有较高的带宽和较大的容量，适用于图形渲染、AI推理等任务
• HBM（High Bandwidth Memory） 主要用于高端计算GPU（A卡、H卡等），如用于AI训练、HPC（高性能计算）和数据中心的GPU，具有更高的带宽和更低的功耗

虽然GPU还包含SRAM（如寄存器、L1缓存、L2缓存），但这些通常被称为缓存，而不是显存。显存特指VRAM，即GPU上的DRAM部分。

GPU中的内存传输

在GPU的运行过程中，将数据从DRAM（VRAM）传输到SRAM是一项“代价高昂”的操作，因为这涉及到不同速度内存之间的数据搬运，会消耗较多的时间和资源。因此，在进行内核优化时，重点之一便是尽可能减少此类数据传输的次数。在AI和渲染等对性能要求极高的任务场景中，高效合理地使用内存，能够显著提升GPU的整体运行表现。



2.2 SIMD 与 SIMT

SIMD（Single Instruction Multiple Data，单指令多数据）指令是一种 并行计算 技术，它允许一个指令同时对多个数据进行相同的运算。

SIMD 的基本概念

传统的 标量（Scalar）计算 是一次对单个数据进行操作：

假设我们有两个数组：
A = [1, 2, 3, 4]
B = [5, 6, 7, 8]
将它们逐个相加，得到：
C = [6, 8, 10, 12]

for (int i = 0; i < 4; i++) {
    C[i] = A[i] + B[i];  // 每次循环只处理 1 个数据
}

逐个元素进行加法：
C[0] = A[0] + B[0];  // 一条指令
C[1] = A[1] + B[1];  // 一条指令
C[2] = A[2] + B[2];  // 一条指令
C[3] = A[3] + B[3];  // 一条指令

 SIMD 指令则 一次操作多个数据：把多个元素打包成一个“向量”，然后一条指令就可以同时处理这 4 个加法：

C[0..3] = A[0..3] + B[0..3]; // 一条 SIMD 指令同时处理 4 个数据

这样可以减少指令数量，提高计算效率。



不同的 CPU 架构支持不同的 SIMD 指令集，主要有：

• x86 架构（Intel/AMD）
  • SSE（Streaming SIMD Extensions）：SSE2、SSE3、SSE4
  • AVX（Advanced Vector Extensions）：AVX、AVX2、AVX-512（512-bit）
• ARM 架构
  • NEON（适用于 ARM 处理器）
  • SVE（Scalable Vector Extension）（ARM 服务器级）
• RISC-V
  • RVV（RISC-V Vector Extension）（灵活的向量长度）



SIMT 与 GPU 并行计算

GPU 不直接 使用 CPU 级的 SIMD 指令（如 AVX、SSE、NEON），但 GPU 的 执行模型 本质上是一种 SIMD 变体，称为 SIMT（Single Instruction Multiple Threads）。两者都是并行计算的，它们的核心思想都是将相同的指令广播给多个执行单元，提高计算效率。

• SIMD（Single Instruction Multiple Data，单指令多数据）——指令级并行（所有计算单元执行相同指令）
  • 所有数据并行执行相同的指令：一条指令作用于多个数据元素，所有计算单元必须执行完全相同的操作
  • 主要依赖于数据向量（vector）进行计算
  • 所有计算单元必须执行同样的指令，如果某个数据元素不需要执行该指令，则会浪费计算资源
  • 适用于数据结构高度规整，并且每个数据点执行相同操作的情况
• SIMT（Single Instruction Multiple Threads，单指令多线程）——线程级并行（线程可以选择执行或不执行）
  • 所有线程执行相同指令，但可以有不同的执行路径，以 线程 为基本执行单元
  • 每个线程有自己的寄存器状态、指令地址计数器（PC，Program Counter），这意味着不同线程可以独立执行不同的计算
  • 支持线程分支（Warp Divergence）：在执行过程中，如果线程内有不同的分支，它们可以选择是否执行指令，而不会影响其他线程的执行

假设有一个线程组在计算：

if (threadIdx.x % 2 == 0) {
    c[threadIdx.x] = a[threadIdx.x] + b[threadIdx.x]; // 偶数线程执行加法
} else {
    c[threadIdx.x] = a[threadIdx.x] * b[threadIdx.x]; // 奇数线程执行乘法
}

在 SIMD 体系下，这是无法做到的，因为 SIMD 要求所有计算单元必须执行相同的操作。但在 SIMT 下，每个线程都可以根据 threadIdx.x 选择不同的计算路径。



GPU架构发展

架构	发布年代	CUDA Cores/SM	总 SM 数	CUDA Cores	L1 + Shared Cache（KB）	L2 Cache(KB)
Tesla	2006	8	16	128	-	-
Fermi	2010	32	16	512	48	768
Kepler	2012	192	15	2880	48	1536
Maxwell	2014	128	24	3072	96	2048
Pascal	2016	64	60	3840	64	4096
Volta	2017	64 CUDA + 8 Tensor	80	5120 CUDA + 640 Tensor	与共享内存共用（最多 96）	6144
Turing	2018	64 CUDA + 8 Tensor	72	4608 CUDA + 576 Tensor	与共享内存共用（最多 96）	6144
Ampere	2020	64 CUDA + 4 Tensor	108	6912 CUDA + 432 Tensor	与共享内存共用（最多 164）	40960
Ada Lovelace	2022	128 CUDA + 4 Tensor	144	18432 CUDA + 576 Tensor	与共享内存共用（最多 128）	9830
Hopper	2022	128 CUDA + 4 Tensor	144	18432 CUDA + 576 Tensor	与共享内存共用 256	61440

* 注：Ada 架构如 AD102（用于 RTX 4090）含 144 SMs、18432 CUDA 核心，但实际启用的数量取决于具体型号。例如 RTX 4090 启用了 128 个 SM，总 CUDA 核心数为 16384。

在 2017 年，NVIDIA 在 Volta 架构的 GPU（如 Tesla V100）中首次引入了 Tensor Core 技术。Volta Tensor Core 支持 FP16 和 INT8 数据类型，后续的 Turing、Ampere、Hopper 等架构进一步改进和扩展了 Tensor Core 的功能。例如，Turing 架构的 Tensor Core 增加了对 INT4 数据类型的支持，Ampere 架构引入了 BF16（Brain Floating Point 16）数据类型，以更好地满足深度学习模型的训练需求。

Tensor Core

Tensor Core，张量核心，在深度学习中，张量是一个多维数组，Tensor Core就是 NVIDIA 推出的为这种多维数组计算而优化的硬件，集成于较新的 GPU 架构中（Volta及之后的架构）。

其主要功能是执行神经网络中的矩阵乘法和卷积运算，通过利用混合精度计算和张量核心操作，Tensor Core 能够在较短的时间内完成大量矩阵运算，从而显著加快训练和推断过程。具体来说，Tensor Core 采用半精度(FP16)作为输入和输出，并利用全精度(FP32)进行存储中间结果计算，以确保计算精度的同时最大限度地提高计算效率。

混合精度训练实际上是一种优化技术，它通过在模型训练过程中灵活地使用不同的数值精度来达到加速训练和减少内存消耗的目的。具体来说，混合精度训练涉及到两个关键操作：

1. 计算的精度分配：在模型的前向传播和反向传播过程中，使用较低的精度（如 FP16）进行计算，以加快计算速度和降低内存使用量。由于 FP16 格式所需的内存和带宽均低于 FP32，这可以显著提高数据处理的效率。

2. 参数更新的精度保持：尽管计算使用了较低的精度，但在更新模型参数时，仍然使用较高的精度（如 FP32）来保持训练过程的稳定性和模型的最终性能。这是因为直接使用 FP16 进行参数更新可能会导致训练不稳定，甚至模型无法收敛，由于 FP16 的表示范围和精度有限，容易出现梯度消失或溢出的问题。

Tensor Core就是专门设计来加速FP16计算的，同时保存FP32的累加精度，从而使混合精度训练成为可能。

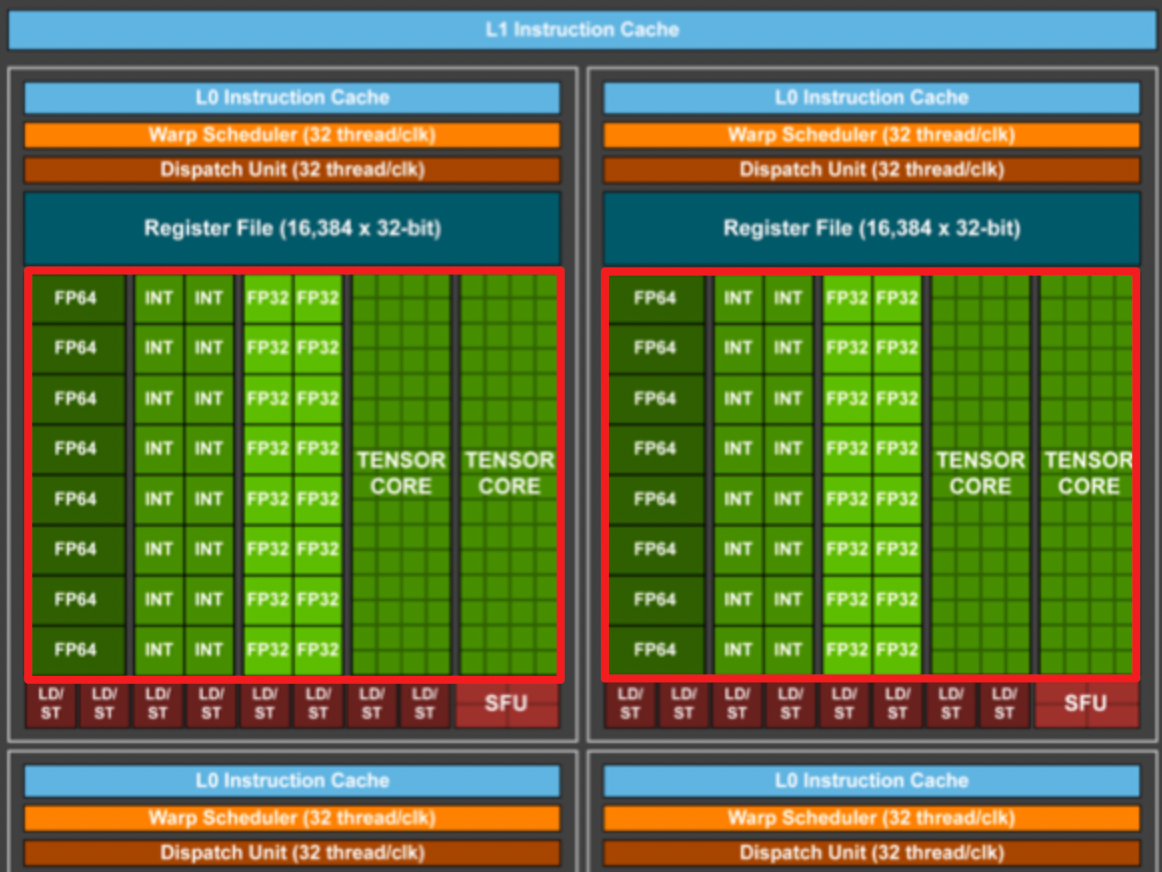
在 Tensor Core 出现之前，CUDA Core 是实现深度学习加速的核心硬件技术。CUDA Core 可以处理各种精度的运算。如上图 Volta 架构图所示，左侧有 FP64、FP32 和 INT32 CUDA Cores 核心，右侧则是许多 Tensor Core 核心。

• CUDA Core
  • CUDA Core 在执行这些操作时，需要将数据在寄存器、算术逻辑单元（ALU）和寄存器之间进行多次搬运，这种过程既耗时又低效。此外，每个 CUDA Core 单个时钟周期只能执行一次运算，而且 CUDA Core 的数量和时钟速度都有其物理限制，这些因素共同限制了深度学习计算性能的提升
• Tensor Core
  • 相较于 CUDA Core，Tensor Core 能够在每个时钟周期内执行更多的运算，特别是它可以高效地完成矩阵乘法和累加操作两种操作是深度学习中最频繁和计算密集的任务之一

	Tensor Core	CUDA Core
设计目标	专为高效的矩阵运算（如矩阵乘法）设计	通用计算单元，支持各种并行计算任务
计算能力	专注于矩阵乘法累加（MMA）操作	支持标量和矢量运算
硬件优化	针对矩阵运算进行了硬件优化，支持混合精度计算	通用硬件设计，适用于各种计算任务
计算吞吐量	极高的矩阵运算吞吐量（如 FP16 MMA）	较低的标量和矢量运算吞吐量
计算精度	支持混合精度计算（如 FP16, BF16, INT8 等）	支持单一精度计算（如 FP32, FP64 等）
适用任务	矩阵乘法、卷积、深度学习训练和推理	通用并行计算任务（如物理模拟、图像处理等）
硬件单元	专用硬件单元，集成在 GPU 中	通用硬件单元，构成 GPU 的基本计算核心
并行级别	以 Warp 或 Warp Group 为单位执行矩阵运算	以线程为单位执行标量和矢量运算
内存访问	优化了矩阵数据的加载和存储(TMA)	支持各种内存访问模式（全局内存、共享内存等）
编程接口	使用 WMMA API 或 CUDA C++ 扩展	使用标准的 CUDA C++ 编程模型
开发难度	需要了解矩阵运算和混合精度计算	相对简单，适用于各种并行计算任务
优化技巧	优化矩阵分块、数据对齐和混合精度计算	优化线程协作、内存访问和分支预测

工作原理

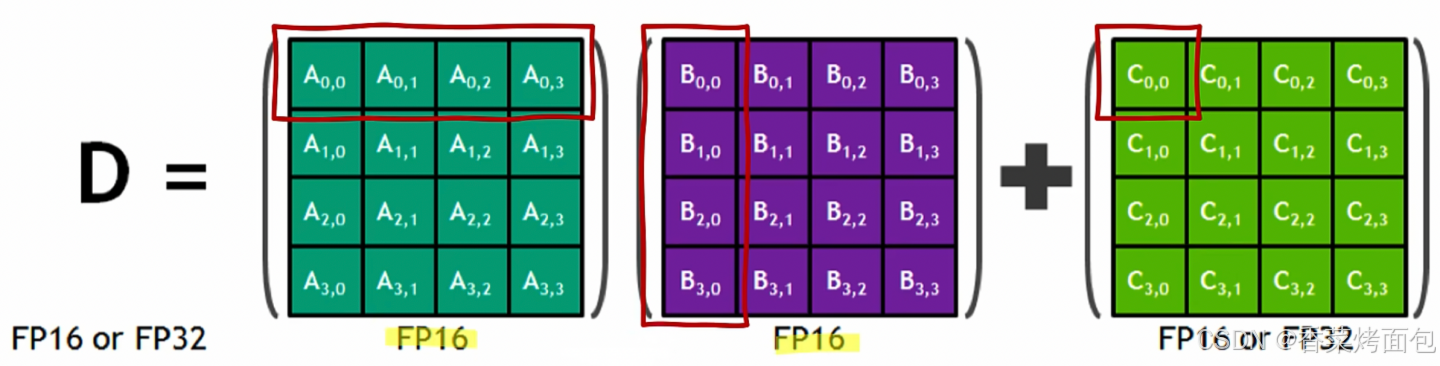
如图所示，深绿色的矩阵是一个 4x4 的矩阵 A，紫色的矩阵是一个 4x4 的矩阵 B，两个矩阵相乘再加上一个绿色的矩阵 C。所谓混合精度就是指在计算的过程当中使用 FP16 去计算，但是存储的时候使用 FP32 或者 FP16 进行存储。

通常在真实的数学计算时，是把矩阵 A 的一行乘以矩阵 B 的一列然后再加上矩阵 C 的单独一个元素得到 D 矩阵的一个元素，以此类推，每一行和每一列相乘得到所有的元素。其中，输入 A 和 B 是 FP16 矩阵，而累加矩阵 C 和 D 可以是 FP16 或 FP32 矩阵

这也就实现了底层硬件上的混合精度计算，通过将矩阵乘法的输入限定为 FP16 精度，可以大幅减少所需的计算资源和内存带宽，从而加速计算。同时，通过允许累加矩阵 C 和输出矩阵 D 使用 FP32 精度，可以保证运算结果的准确性和数值稳定性。这种灵活的精度策略，结合 Tensor Core 的高效计算能力，使得在保持高性能的同时，还能有效控制神经网络模型的训练和推理过程中的资源消耗。

然而在英伟达的 GPU Tensor Core 中并不是一行一行的计算，而是整个矩阵进行计算，核心思想是 批量并行计算，而不是传统的 按行-列计算，是矩阵块（tile-based）计算，一次性完成多个乘加操作，可以看看官方给出的 Tensor Core 的计算模拟图：

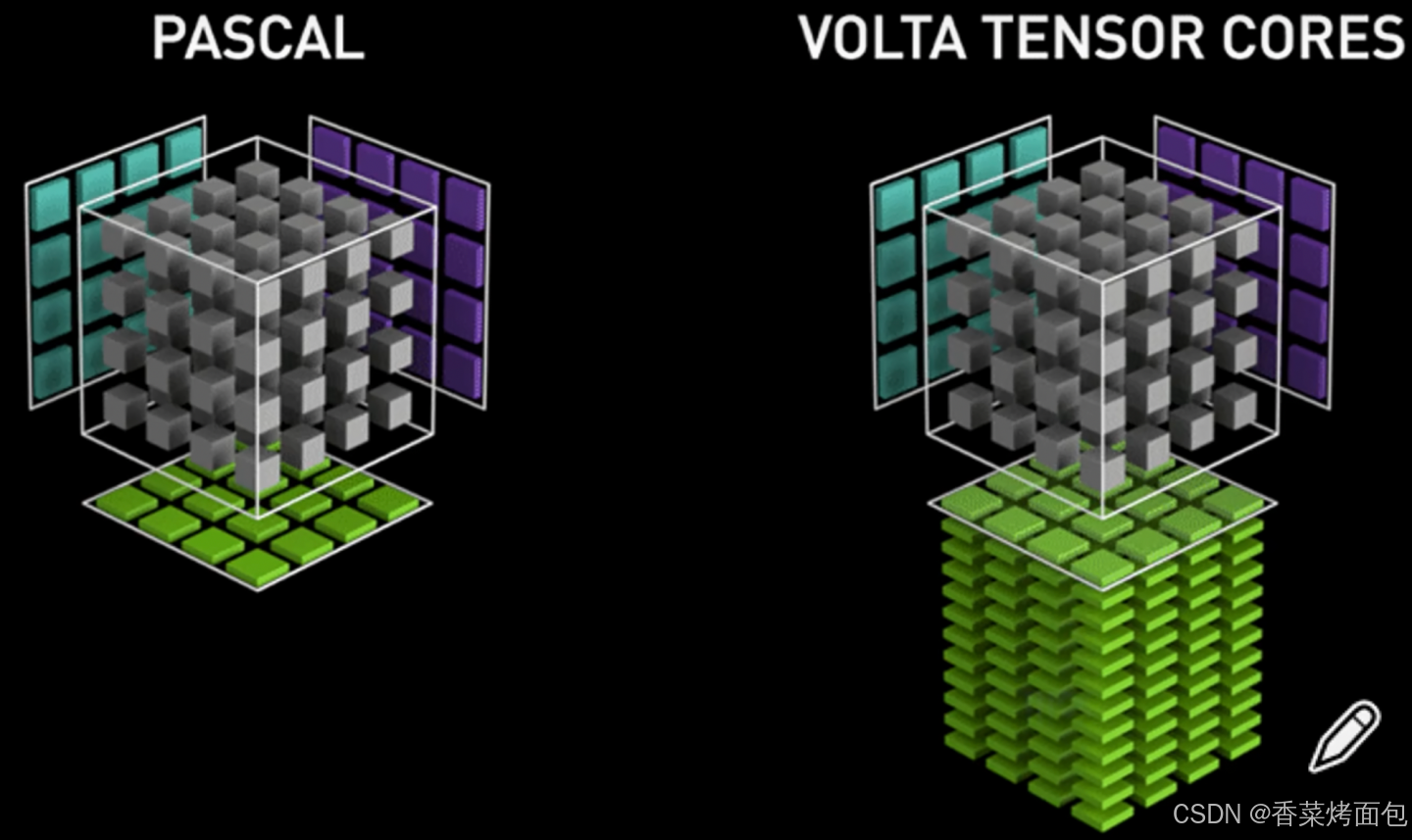
• 左边为没有 Tensor Core 的 Pascal 架构，其运行原理是一个元素跟一行进行相乘，每个时钟周期执行 4 次相乘得到一列的数据
• 右边则为具有 Tensor Core 的 Volta 的架构，其 Tensor Core 计算的过程是把整个矩阵 A 和矩阵 B 进行相乘然后得到一个矩阵的输出，右边 Tensor Core 在单个时间周期内就能够执行4 * 4 * 4等于64次的乘加的计算操作

⁉️ 单独计算需要计算64次，Tensor Core 为什么能在一个周期内完成？

1. Tensor Core 是专为矩阵块乘法设计的硬件单元，不像传统的 ALU 一次处理一个 FMA
2. 它内部有 高度并行的乘加单元阵列，专门负责同时处理多个数对
3. 对于 4×4×4 的 tile，Tensor Core 在硬件上一次“调度”（issue）就可以触发所有 64 个乘加操作的执行
4. 每一个操作其实都是 FMA（Fused Multiply-Add），也就是说，它不是单纯乘法再加法，而是 一个乘法 + 一个加法 被融合成一个操作，在硬件层效率更高



Tensor Core 内部使用 FP32 进行累加，最终存储在 FP16，会因为截断导致精度下降，NVIDIA H100 引入了 FP8 格式（E5M2 / E4M3），在累加时会带来更大的舍入误差。Tensor Core 采用 Warp-Level 并行计算，数据在 tiles（小块）之间传输和计算，当多个 tiles 结果累加时，数值的重新排列可能导致不同的累加误差，如何减少精度丢失？

• 使用 FP32 进行累加：如 FP16 × FP16 支持 FP32 accumulation，减少舍入误差
• 对于大规模累加操作，可以先累加较小的值，再累加较大的值，以减少误差累积
• 在 A100 / H100 上，TF32 具备 10-bit 尾数（TF32 目前只在Ampere和Hopper架构支持），相比 FP16 更精确，可减少累加误差



⁉️ 一个 Tensor Core 每个周期可以执行 4x4x4 的 GEMM 运算。然而，在 CUDA 的层面，为什么提供了使用 16x16x16 的 GEMM 运算 API 呢？

✅ 实际上，在一个 SM（Streaming Multiprocessor）中有多个 Tensor Core，无法对每个 Tensor Core 进行细粒度的控制，否则效率会很低。因此，一个 Warp 将多个 Tensor Core 打包在一起，以执行更大规模的计算任务。通过 Warp 层的卷积指令，CUDA 向外提供了一个 16x16x16 的抽象层，通过一条指令完成多个 Tensor Core 的协同工作，实现高效的并行计算。



⁉️ 那么现在有一个问题，Tensor Core 是如何跟卷积计算或者 GEMM 计算之间进行映射的呢?

例如 GPU 中的 Tensor Core 一次仅仅只有 4x4 这么小的 kernel，怎么处理 input image 224*224，kernel 7*7 的 GEMM 计算呢?

或者说在大模型中，Tensor Core 是怎么处理 Transformer 结构 input embedding 为 2048*2048、8192*8192的层的 GEMM 呢?

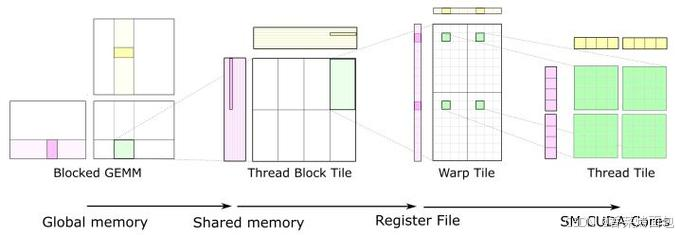
• Blocked GEMM
  • 粉色、黄色部分是矩阵 A 和 B 的一部分，整个矩阵存储在 全局内存（Global Memory） 中
  • 由于显存（global memory）访问慢，GPU 不会直接用全局内存计算，而是采用 分块（Blocking） 方式，从全局内存中取出小块数据
• Thread Block Tile
  • 每个 线程块（Thread Block） 负责处理矩阵乘法中的一个子块
  • 粉色、黄色片段 被加载到 共享内存（Shared Memory），共享内存比全局内存快很多，减少了访存延迟
• Warp Tile
  • 线程块内部进一步划分，数据被分配给 Warp，粉色、黄色片段 进一步拆分成 Warp 级的计算片段
  • 这些数据存储在 寄存器（Register File） 中，计算速度极快
• Thread Tile
  • Warp 内部的线程计算更小的片段，最终传递到 CUDA 核心，Tensor Core 直接执行 4×4×4 FMA（乘加）运算

如上图所示，从左到右，计算的数据块逐渐变小，计算粒度逐渐细化，最终适配 CUDA 核心计算，在 Tensor Core 以 4×4×4 的方式完成

3. 常见的GPU矩阵计算库

3.1 cuBLAS 库

• BLAS是一组常用的低级线性代数运算，如向量和矩阵乘法、线性方程组的求解等。cuBLAS 通过利用 GPU 的并行计算能力，能显著加速这些运算
• cuBLAS 是 NVIDIA 推出的基于 CUDA 的并行计算库，专门针对矩阵运算（BLAS）进行优化，cuBLAS 作为 CUDA Toolkit 的一部分，安装 CUDA 后即可直接使用

cuBLAS接口可以分为三类：

• cuBLAS API要求应用程序矩阵和向量数据必须使用GPU内存
• cuBLASXt API允许应用程序把数据保存在主机内存，再通过用户请求把主机内存的数据传输到一个或多个GPU上
• cuBLASLt API是适用于GEMM（GEneral Matrix-to-matrix Multiply）操作的轻量级库，在数据分布、输入类型、可变参数等方面上更具灵活性



cuBLAS 的计算流程

调用 cublasSgemm() 或 cublasGemmEx()，cuBLAS 会：

1. 检测 Tensor Core 是否可用

• 如果数据类型是 FP16, BF16, TF32，就会使用 Tensor Core
• 否则，会用 CUDA Core 进行普通矩阵运算

2. 选择最优 Kernel

• cuBLAS 内部有多个不同的 Kernel，比如：Tiled GEMM（使用共享内存优化）、Strided Batched GEMM（适用于小批量计算）、Tensor Core GEMM（最大化吞吐量）
• 根据 矩阵大小 和 GPU架构 选择最优实现

3. 优化内存访问

• cuBLAS 采用 column-major（列优先存储），保证数据访问连续性
• 使用 Shared Memory 缓存部分 A 和 B 矩阵，减少全局内存访问
• 采用 数据预取（Prefetching），隐藏数据加载延迟

4. 执行计算

• 使用 Warp-level 计算：一个 Warp（32个线程） 处理一个 Tile（块），使用 Tensor Core 计算 16×16 子矩阵
• 计算完成后，将结果写入全局内存

cuBLAS 关键优化

优化方式	作用
Tensor Core	使用 Warp Matrix Multiply-Accumulate（WMMA），提高吞吐量
Tiled GEMM	让每个 Thread Block 处理一个 Tile，提高并行度
Shared Memory Buffering	预加载 A 和 B 子矩阵，减少全局内存访问
Prefetching	预取数据，隐藏数据加载延迟
Stream Execution	允许多个 GEMM 操作并行执行，提高 GPU 利用率



3.2 Cutlass 库

Cutlass 是 NVIDIA 开源的 高性能 GEMM 库，它本质上是 cuBLAS 的底层实现之一，但提供了 可定制的 API，可以让开发者自己实现高性能 GEMM。

Cutlass 计算流程

Cutlass 采用 分层架构，包括：

1. Thread Block 级计算

• 采用 Tile-based GEMM，让 每个 Block 负责计算一个子矩阵
• 使用 共享内存 加速计算

2. Warp 级计算

• 每个 Block 内有多个 Warp，每个 Warp 计算一个 8×8 或 16×16 子矩阵
• 如果 GPU 支持 Tensor Core，则使用 WMMA（Warp Matrix Multiply-Accumulate） 指令

3. Thread 级计算

• 每个 Thread 计算 4×4 或更小的矩阵块，并进行最终累加

Cutlass 关键优化

优化方式	作用
Tile-based GEMM	让 GPU 计算子矩阵，提高数据局部性
Pipeline 计算	计算和数据加载并行，提高吞吐量
Tensor Core 支持	直接使用 Tensor Core 加速计算
编译时优化	Cutlass 允许开发者指定 Tile 大小，最大化 GPU 资源利用率
线程 Warp 级别计算	让 Warp 计算 16×16 子矩阵，提高 Warp 利用率

 

cuBLAS vs Cutlass

• cuBLAS 是 NVIDIA 官方库，适用于 所有 GPU，内部优化了 内存访问、计算模式、并行度，能够自动调用 Tensor Core 进行计算
• Cutlass 是 cuBLAS 的底层实现之一，提供了 更高的定制性，适用于 自定义计算需求，比如 FP8、BF16、混合精度计算等

特性	cuBLAS	Cutlass
易用性	✅ 调用简单 cublasGemmEx()	❌ 需要自己写 Kernel
性能	✅ 最优（自动调优）	✅ 也很快，但需要手动调优
定制性	❌ 只能使用官方 API	✅ 可定制，支持不同数据格式
适用场景	高性能深度学习、数值计算	需要自己实现高性能 GEMM 的应用

• cuBLAS (CUDA Basic Linear Algebra Subprograms) 基于 CUDA，用于加速通用线性代数运算，并不局限于深度学习。
• cuTLASS 主要提供高效的矩阵乘法（GEMM）实现。它把 cuDNN、 cuBLAS 中的矩阵乘法优化抽象为 C++ 模板类，用户可以像“搭积木”一样定制自己的高效矩阵乘法，开发出性能和 cuDNN、 cuBLAS 相当的线性代数算子



两者之间如何选择？

• cuBLAS与cuTLASS的对比
  • cuBLAS 是闭源的，用户只能调用，但不知道内部细节，更不能扩展；
  • cuTLASS 是开源的，用户可以自己定制和优化算子，而且开源社区提供了很多算法解释以及实现代码。
• 如何选择？
  • 如果只想找一个 API 函数，cuBLAS 就够了；如果想进一步根据具体的场景和问题优化矩阵乘法，需要用 cuTLASS 定制你的算子



3.3 DeepGEMM

一个FP8 GEMM（通用矩阵乘法）库，支持密集（dense）和混合专家（MoE）矩阵乘法运算

• 稠密矩阵乘法：最常见的GEMM类型，适用于大多数深度学习模型（卷积操作、全连接层等）
• 稀疏矩阵乘法：用于处理包含大量零元素的矩阵，通常用于自然语言处理等任务



DeepGEMM 做了什么?

1. FP8 支持优化

• DeepGEMM 主要针对 FP8 优化，相比 FP16 计算 可以减少 2 倍的内存带宽需求（‌Tensor Core‌ 的 TF32 格式通过降低精度实现计算加速，但仍需 FP16/FP32 存储中间结果，带宽压力未根本解决‌）
• 支持 FP8 输入，但累加到 FP16 或 FP32，减少数值精度损失，同时保持 FP8 的高吞吐量优势

方案	支持数据类型	优势
传统 GEMM	FP32, FP16	适用于通用矩阵乘法，但内存带宽需求较高
Tensor Core GEMM	FP32, FP16, TF32	计算更快，但 FP16 仍然受带宽限制
DeepGEMM	FP8（累加到 FP16 / FP32）	减少 2× 内存带宽，优化数据访问，提高吞吐量

2. 支持分组GEMM

DeepGEMM支持的GEMM类型:

• 常规稠密 GEMM：通过函数 deep_gemm.gemm_fp8_fp8_bf16_nt 调用，适用于常规矩阵乘法。
• 分组 GEMM（连续布局，Contiguous Layout）：针对 MoE 模型优化，仅对 M 轴分组，N 和 K 保持固定。这种设计适用于 MoE 专家共享相同形状的情况。将多个专家的 token 拼接成单一连续张量，适用于训练前向或推理预填充阶段。每个专家段需对齐到 GEMM 的 M 块大小。
• 分组 GEMM（掩码分组，Masked Grouped GEMM）：支持推理解码阶段，结合 CUDA Graph，适应动态 token 分配。这种分组策略与 CUTLASS 的传统分组 GEMM 不同，体现了 DeepGEMM 对 MoE 模型的针对性优化。

3. 调度优化

TMA 加速

DeepGEMM为什么只支持Hopper架构呢？就是因为它使用了TMA，通过异步加载减少内存访问延迟，其他GEMM库都没有启用TMA

TMA (Tensor Memory Accelerator)：

• 刚刚说到GPU会将原始矩阵切分为图块并分发给线程块去执行，那么就需要有加载矩阵，GPU的内存结构和CPU的构造有些许不同，并且每代架构似乎也不太相同，但最终目的是一样的，将矩阵加载到线程可以直接使用的地方
• TMA 是 NVIDIA 在 Hopper GPU架 构中引入的一种技术，之前的 Ampere及更早架构不具备这个机制，主要功能是优化矩阵乘法运算，通过异步数据传输和索引计算来提高性能
• TMA采用结构化访问张量数据的方式，使得在写代码时可以让其以按块或特定结构加载数据，同时可以异步批量地加载数据

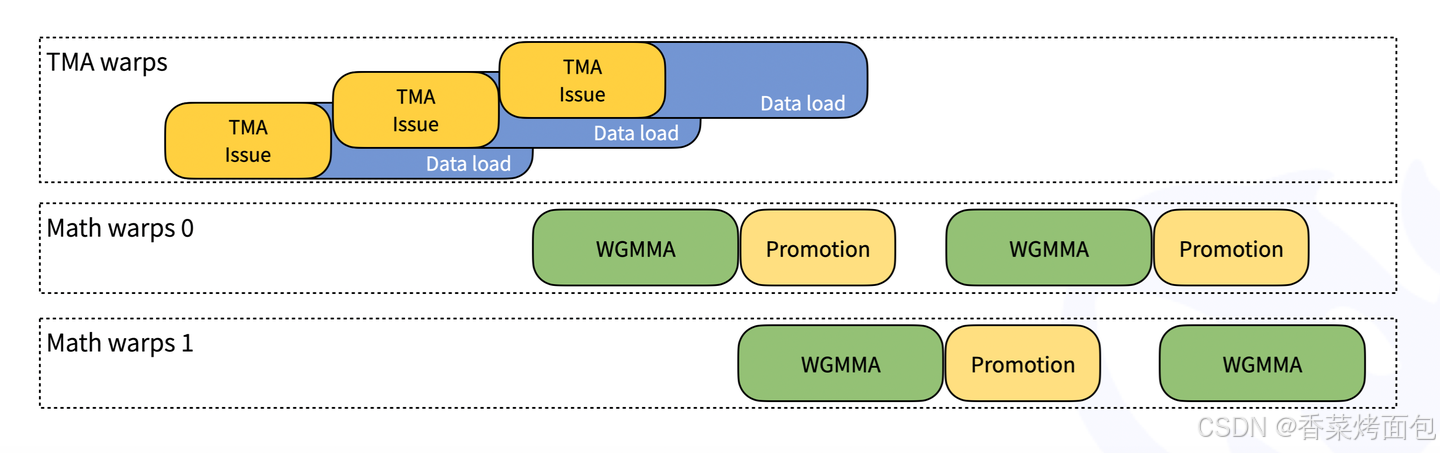
如上图所示，图中分为三个部分：TMA warps（负责数据加载）、Math warps 0（负责矩阵计算）、Math warps 1（负责矩阵计算）。TMA warps中，黄色框（TMA Issue）触发数据加载请求，相当于告诉硬件“我要取数据了”，蓝色框（Data Load）代表数据实际加载的过程，这个过程是 异步的，即 数据加载时，计算仍在继续进行，TMA Issue 与 Data Load 重叠，说明在当前数据加载的同时，可以提前请求下一批数据，避免 GPU 计算线程（math warps）自己去管理数据搬运，计算线程可以专注于计算，访存线程（TMA warps）专注于数据搬运，计算和数据加载完全解耦。Math warps 0和1主要执行TensorCore 矩阵乘法计算，并进行 数据类型转换（Promotion），同时进行计算，说明 DeepGEMM 在不同 warp 之间实现了流水线（pipeline）计算，一个 warp 计算时，另一个 warp 进行数据准备。

指令重叠

内核采用 warp-specialized 设计，允许数据移动、张量核心 MMA（矩阵乘加）指令和 CUDA 核心累加操作重叠

• Warp-specialized 设计
  • 在 GPU 计算中，warp 是 CUDA 线程调度的基本单位，通常由 32 个线程 组成
  • warp-specialized 设计 指的是不同的 warp 负责不同的计算任务（如数据加载、矩阵运算、累加等），通过流水线化机制，warp 之间的计算可以交叠执行，避免资源闲置
• 数据移动
  • 在 GPU 计算中，数据需要从全局内存传输到共享内存 或寄存器，再进入 Tensor Core 计算单元
  • warp-specialized 设计使得数据移动可以和计算部分并行执行，一个 warp 在执行计算时，另一个 warp 可以从全局内存加载数据，避免等待数据传输，提升计算吞吐量
• 张量核心 MMA
  • Tensor Core 使用 MMA 指令，一部分 warp 负责计算 MMA，另一部分 warp 负责预加载数据，让 Tensor Core 保持计算
• CUDA 核心累加
  • 通过 warp-specialized 设计，可以让 Tensor Core 计算和 CUDA Core 累加操作并行执行

区块调度器

通过统一的调度器调度所有非分组和分组内核，栅格化（Rasterization ）以增强 L2 缓存的复用/重用

• Block Scheduler 负责管理计算任务的分配，这里的统一调度器是调度所有类型的 CUDA 内核，包括非分组和分组内核
  • 非分组内核：每个线程块（Block）可以独立运行，不受其他块的影响
  • 分组内核：多个线程块协同工作，可能共享数据或有严格的执行顺序（如 Tensor Core 计算）
  • 统一调度器自动管理这些不同类型的任务，让 GPU 计算资源始终处于高利用率状态，避免某些计算单元空闲或等待数据
• 栅格化与 L2 缓存复用
  • 栅格化是一种 GPU 计算任务分配策略，可以 优化线程块在 SM上的布局
  • L2 缓存存储经常访问的数据，减少全局内存访问
  • 栅格化调度合理分配 Block 位置，使得 相邻线程块共享数据，减少 DRAM 访问，提高整体吞吐量

JIT（即时编译）设计

与其他传统 GEMM 库（如 CUTLASS）需要预编译不同，DeepGEMM 的 JIT 设计允许在运行时动态生成内核。这带来以下优势：

• 灵活性：无需为不同矩阵大小或硬件配置预先编译多个版本
• 简便性：用户安装时无需复杂依赖或编译环境
• 性能优化：JIT 可以根据实际输入动态调整代码，可能提升缓存命中率或指令调度效率

在JIT中：

• GEMM 形状、块大小和流水线阶数被视为编译常量，从而可能获得更多优化
• 可自动选择区块大小、warpgroups 数量、最佳流水线阶段和 TMA cluster大小
• 展开 MMA 流水线，可使编译器进行更多优化



4. GEMM性能测试方法

4.1 cublasMatmulBench

cublasMatmulBench 是 NVIDIA 提供的一个基准测试工具，用于评估 cuBLAS 库中矩阵乘法（GEMM, General Matrix-Matrix Multiplication）的性能。通过调用 cuBLAS 的矩阵乘法接口，测试不同精度（FP16/FP32/INT8 等）、矩阵尺寸和计算模式下的运算速度‌

【⚠️ cublasMatmulBench 工具是 NVIDIA 提供给其合作伙伴，需要签署保密协议才能获取，并未在公开的仓库或 CUDA Samples 中提供】

• 性能评估：测试GPU进行通用矩阵乘法的性能，评估GPU的TFLOPS性能
• 不同精度比较：测试不同精度格式(如FP16、FP32、TF32等)下的性能表现，评估训练和推理性能
• 硬件对比：比较不同GPU型号在矩阵乘法上的性能差异
• 优化指导：测试结果可以反映出硬件的性能瓶颈
• 稳定性测试：长时间运行大规模矩阵乘法，可以测试GPU在高负载下的稳定性
• 新特性验证：验证新GPU架构或CUDA版本带来的性能提升，如Tensor Core加速
• 基准测试：作为标准化的测试工具，可以在不同环境下进行可重复的性能测试，便于横向比较

虽然cublasMatmulBench的结果可能不完全代表实际应用的性能，但它提供了一个很好的基准来展示不同GPU的性能能力，对于硬件选型和性能优化都有重要参考价值。

4.2 BatchCuBlas

BatchCuBlas 是一个基于 CUDA 的数学库，是NVIDIA CUDA Toolkit中一个示例程序，专门用于执行大规模的批量矩阵运算，如矩阵乘法、矩阵-向量乘法和其他矩阵运算。BatchCuBlas 通过将多个矩阵运算合并为一个批处理操作，可以减少CPU与GPU间的通信开销，优化整体的内存访问模式，从而提高性能。

BatchCuBlas 计算流程：

1. 初始化和配置：设置CUDA环境，并为将要执行的矩阵运算初始化数据
2. 数据准备：准备输入数据，通常是一组矩阵，然后将这些数据从主机内存复制到GPU内存
3. 执行批量BLAS运算：使用CUBLAS函数进行批量矩阵运算，如批量矩阵乘法（cublasXgemmBatched）。这些函数接受一组矩阵作为输入，一次性在GPU上并行处理这些矩阵，显著提高运算速度
4. 结果处理：运算完成后，将结果从GPU内存复制回主机内存
5. 性能评估：计算和显示执行所需时间，评估GPU加速的效益

测试方法

cuda驱动中默认不会安装BatchCuBlas库，需要手动安装：

git clone https://github.com/NVIDIA/cuda-samples.git
cd cuda-samples/Samples/4_CUDA_Libraries/batchCUBLAS
make

在 cuda-samples/Samples/4_CUDA_Libraries/batchCUBLAS 目录下 make编译后可以开始测试，主要测试单精度 (sgemm) 和双精度 (dgemm) 计算的执行时间 (elapsed time) 和 GFLOPS（十亿次浮点运算每秒）

• -m8192 设置矩阵 A 的行数和 C 的行数
• -n8192 设置矩阵 B 的列数和 C 的列数
• -k8192 设置矩阵 A 的列数和 B 的行数

日志：

./batchCUBLAS -m8192 -n8192 -k8192 #默认测试为0的GPU卡 --device=1，指定GPU卡
batchCUBLAS Starting...
GPU Device 0: "Hopper" with compute capability 9.0
==== Running single kernels ==== # 单核，单次 GEMM 计算
Testing sgemm # 单精度
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0xbf800000, -1) beta= (0x40000000, 2)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.04718018 sec GFLOPS=23304.5 # GFLOPS（十亿次浮点运算每秒），elapsed 执行时间
@@@@ sgemm test OK # # 每个测试块的结束都会有一个确认消息
Testing dgemm # 双精度
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0x0000000000000000, 0) beta= (0x0000000000000000, 0)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.00027800 sec GFLOPS=3.95513e+06
@@@@ dgemm test OK
==== Running N=10 without streams ==== # 多次测试（N=10），Without Streams（不使用 CUDA Streams 并行）
Testing sgemm
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0xbf800000, -1) beta= (0x00000000, 0)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.21222401 sec GFLOPS=51809
@@@@ sgemm test OK
Testing dgemm
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0xbff0000000000000, -1) beta= (0x0000000000000000, 0)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.18430996 sec GFLOPS=59655.6
@@@@ dgemm test OK
==== Running N=10 with streams ==== # With Streams（使用 CUDA Streams 并行）
Testing sgemm
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0x40000000, 2) beta= (0x40000000, 2)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.21426201 sec GFLOPS=51316.2
@@@@ sgemm test OK
Testing dgemm
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0xbff0000000000000, -1) beta= (0x0000000000000000, 0)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.19183898 sec GFLOPS=57314.3
@@@@ dgemm test OK
==== Running N=10 batched ==== # Batched（批量 GEMM）
Testing sgemm
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0x3f800000, 1) beta= (0xbf800000, -1)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.19998002 sec GFLOPS=54981.1
@@@@ sgemm test OK
Testing dgemm
#### args: ta=0 tb=0 m=8192 n=8192 k=8192 alpha = (0xbff0000000000000, -1) beta= (0x4000000000000000, 2)
#### args: lda=8192 ldb=8192 ldc=8192
^^^^ elapsed = 0.23587298 sec GFLOPS=46614.6
@@@@ dgemm test OK

Test Summary
0 error(s)

结果：

• Running single kernels
• Running N=10 without streams
• Running N=10 with streams
• Running N=10 batched



5. NVIDIA 性能分析工具

• 如何通过性能分析工具定位问题

  • 使用NVIDIA Nsight工具进行性能分析
  • 使用CUDA Profiler对内存使用、计算资源进行优化分析——已被 Nsight 替代，从 CUDA 11.0 开始已被弃用

NVIDIA Nsight

NVIDIA Nsight 是 NVIDIA 的 性能分析和调试工具（新一代 profiling 工具，支持 Pascal 及以后显卡），可以简单地理解为一种帮助用户查看和理解用到GPU程序在计算机上如何运行的工具，如下图，Nsight 有很多 SDK：

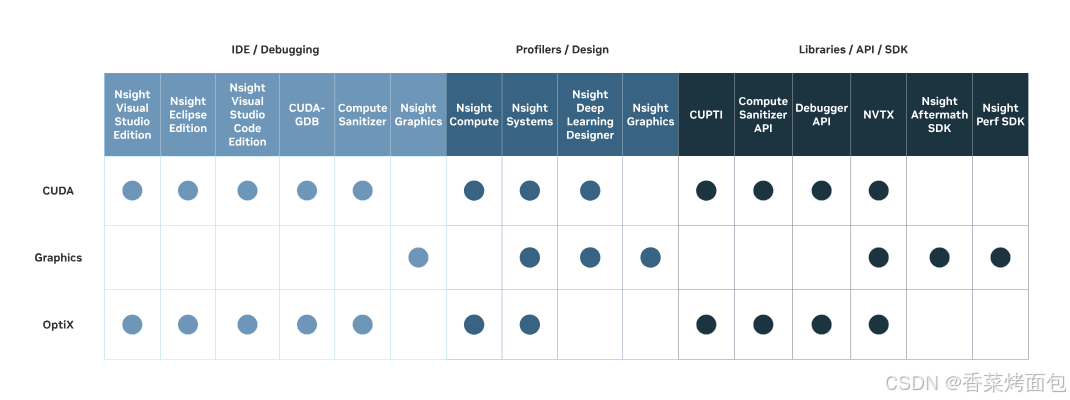
• Nsight Systems 是系统级别的性能分析工具，记录程序在运行过程中的各种信息，如每个任务的开始和结束时间、GPU的利用率、内存使用情况等
• Nsight Compute 内核级（Kernel）分析，针对 Kernel 函数的详细性能分析工具

工作流：先用nsight system做全局的分析，如果需要看kernel内部的profile再用nsight compute



Nsight Systems(nsys)

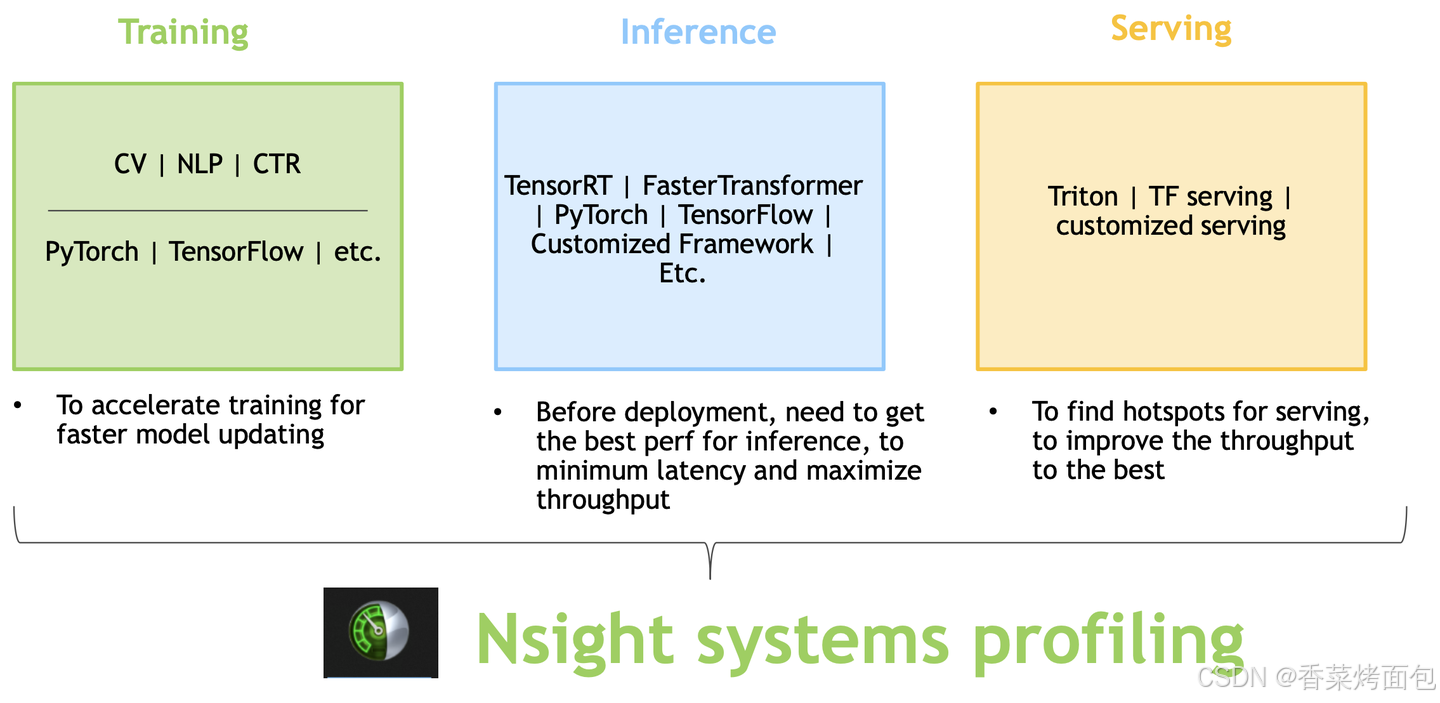
主要功能：

• 系统级分析：Nsight Systems 能够捕获和分析整个系统的性能数据，包括 CPU 和 GPU 的活动、内存使用情况、线程调度、I/O 操作等
• 时间轴视图：提供详细的时间轴视图，展示不同时间点上系统中各个组件的活动情况，通过时间轴视图直观地看到 CPU 和 GPU 任务的执行时间、数据传输时间等
• API 跟踪：能够跟踪各种 API 调用，如 CUDA API、NVTX（NVIDIA Tools Extension）标记、操作系统线程调度等，了解程序的执行流程和时间开销

NVTX是 NVIDIA 提供的一种 标记（instrumentation）工具，类似于日志，在代码执行时插入一个时间点，方便后续分析。例如用于标记一段代码的开始和结束，在 Nsight Systems 中可以看到该代码块的运行时间。

安装了CUDA Toolkit，那么 ${CUDA_HOME}/bin/nsys 就是 nsight system 的可执行程序，它可以分为两部分，服务器上的性能测试工具用于生成程序运行报告，以及各种平台都可用的可视化工具用于可视化报告。

安装

官网下载：Nsight Systems - Get Started | NVIDIA Developer

# 可通过 NVIDIA CUDA Toolkit 安装：
sudo apt-get install nsight-systems
# 使用官网下载的 .run 安装包
sudo sh ./nsight-systems-2024.1.1-linux-x64-installer.run

使用方法

nsys profile -o report_name ./program

• profile 是 Nsight Systems 的主要命令，表示进行性能分析
• -o report_name 表示生成的报告文件名
• ./program 是要分析的可执行程序

这个命令会生成一个 .qdrep 文件格式的报告文件，它包含详细的性能数据，可在 Nsight Systems GUI 里查看

参数说明

可用参数：User Guide — nsight-systems 2025.3 documentation

常用参数：

参数	作用
-o <file>	指定输出文件名，默认 .qdrep 格式
--export=json,csv	以 JSON 或 CSV 格式导出数据
--trace	选择跟踪的API，可以选择多个API，用逗号分隔（可选 cuda, nvtx, cublas, cublas-verbose, cusparse, cusparse-verbose, cudnn, cudla, cudla-verbose, cusolver, cusolver-verbose, opengl, opengl-annotations, openacc, openmp, osrt, mpi, nvvideo, vulkan, vulkan-annotations, dx11, dx11-annotations, dx12, dx12-annotations, openxr, openxr-annotations, oshmem, ucx, wddm, tegra-accelerators, python-gil, syscall, none 等），默认cuda, opengl, nvtx, osrt
--stats‌=true	生成汇总统计数据（如CUDA API调用次数、内存复制耗时、内核执行时间等）
--delay=5	分析开始前的延迟时间（5秒）
--gpu-metrics-device=all	启用GPU指标采样（如SM利用率、显存带宽等），--gpu-metrics-device=0 采集设备0的GPU指标
--cpu-sampling=true	采集 CPU 采样信息
--sample=cpu / none（禁用）	启用或禁用 CPU 采样
--cuda-memory-usage=true	记录 CUDA 设备内存使用情况
--cuda-graph-trace=true	记录 CUDA Graph 相关事件
--cuda-api-trace=true	跟踪所有 CUDA API 调用
--cuda-kernel-trace=true	记录所有 CUDA Kernel 运行情况

使用示例

nsys profile -o cosyvoice_output_profile --trace=cuda,nvtx,cudnn,cublas --force-overwrite true --stats=true python3 test.py

Nsight Compute(ncu)

Nsight Compute 是 CUDA 核心（Kernel）级分析工具，分析 CUDA 内核执行效率、寄存器/访存/算力利用率，用于内核级分析，优化 CUDA Kernel 执行效率。

安装

官网下载：Getting Started with Nsight Compute | NVIDIA Developer

sudo apt-get install nsight-compute
# .run 安装包
sudo sh ./nsight-compute-2024.1.1-linux-x64-installer.run

使用方法

# 对某个 CUDA Kernel 进行分析
ncu --set full -o report_name ./program

参数说明

可用参数：4. Nsight Compute CLI — NsightCompute 12.9 documentation

常用参数：

参数	作用
--export <file>	导出结果到文件
--csv	以 CSV 格式输出数据
--json	以 JSON 格式输出数据
--launch-skip <n>	跳过前 n 次 Kernel 执行
--launch-count <n>	分析前 n 次 Kernel 执行
--section <name>	选择分析的部分，（如 --section=SpeedOfLight 分析计算/内存吞吐瓶颈）
--set <profile-set>	full（全面分析）、memory（内存分析）、compute（计算分析）
--target-processes	分析的进程范围，常用 all（捕获所有CUDA进程）
--metrics <metric-list>	指定要分析的 GPU 指标，如 sm__cycles_elapsed.avg, dram__throughput.avg
--kernel-regex‌	过滤需分析的内核（通过正则表达式匹配内核名称），--kernel-regex="matmul" 仅分析名称含 matmul 的内核
--sampling-interval <ms>	采样间隔（毫秒）
--nvtx	采集 NVTX 事件

style="display: none !important;">