论文阅读：Meta structure: Computing relevance in large heterogeneous information networks

       前面有读过关于异构信息网络(Heterogeneous information network, HIN)的另一篇论文：PathSim。PathSim中有个定义叫元路径(Meta Path)，这次这篇论文呢，提出了一个新的定义，叫元结构(Meta Structure)，元结构可以说是对元路径的一种扩充。下面还是以经典异构信息网络——文献信息网络(bibliography Information Network)作为例子。当然，这里没有原文中介绍的那么详细，加了一些我自己的见解，我之前也有过介绍PathSim，下面的介绍默认读者读过PathSIm这篇文章。

定义1.元结构(Meta Structure)是定义在AHIN的网络模式SG=(A,R)上的，以HIN为模板的有向图，它有一个起始节点ns（入度为0）和一个目标节点nt（出度为0）。S=(N,M,ns,nt)，其中N是点集，M是边集。如果x∈N，则x∈A；如果(x,y)∈M，则(x,y)∈R。

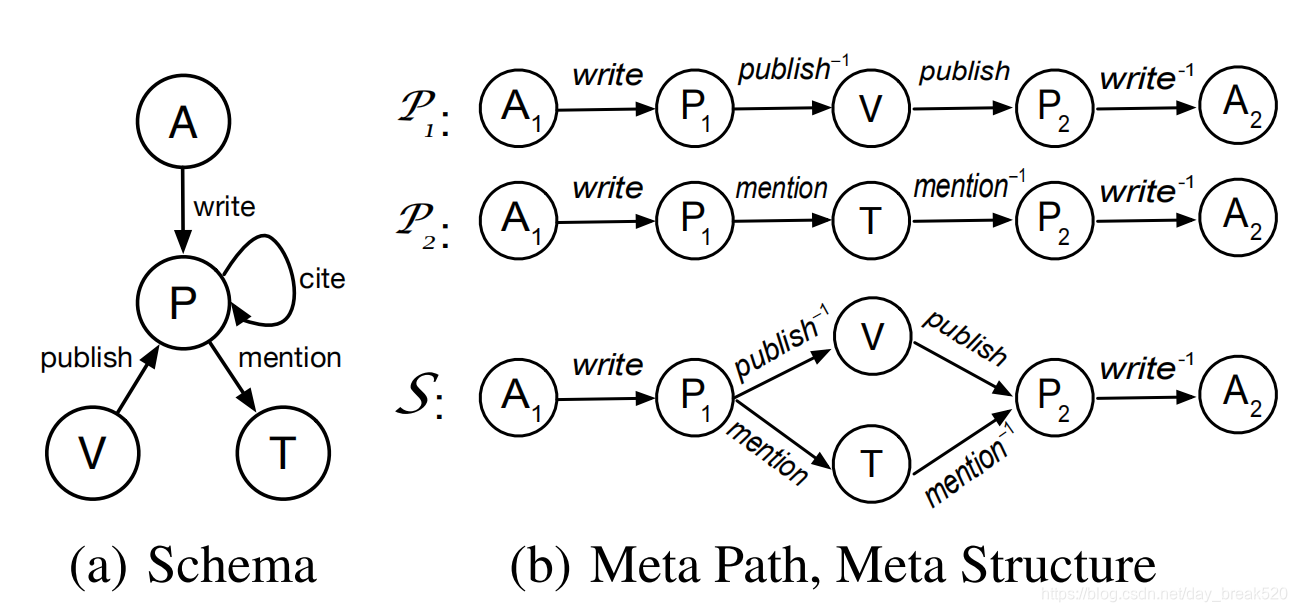
       上图(a)是文献信息网络的Schema，(b)的P1，P2是文献信息网络的两个元路径实例（之前的博客也有说过，异构信息网络中元路径的结构不是唯一的），(b)中的S就是一个元结构实例，直观的看上去，元结构S把元路径P1，P2合二为一了，所以说，在这个例子中，元结构能够比元路径表示更多的信息。元结构比元路径复杂了一些，所以在利用HIN进行相似度计算的方面，在理解上元结构要比元路径复杂一些。

定义2.ETree.在给出HIN、元结构S和起始节点os的基础上，定义ETree=(T,L,w)，其中：

           ·T代表ETree的节点集合，每一个节点是AHIN展开结构的子图。

           ·L是边集；

           ·w()函数将树的节点v∈T映射到其权重w(v)。w(v)是基于v的父节点u，即(u, v) ∈ L。

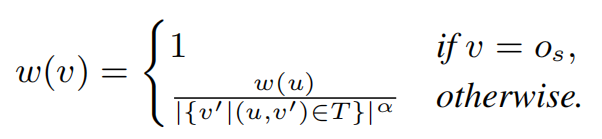
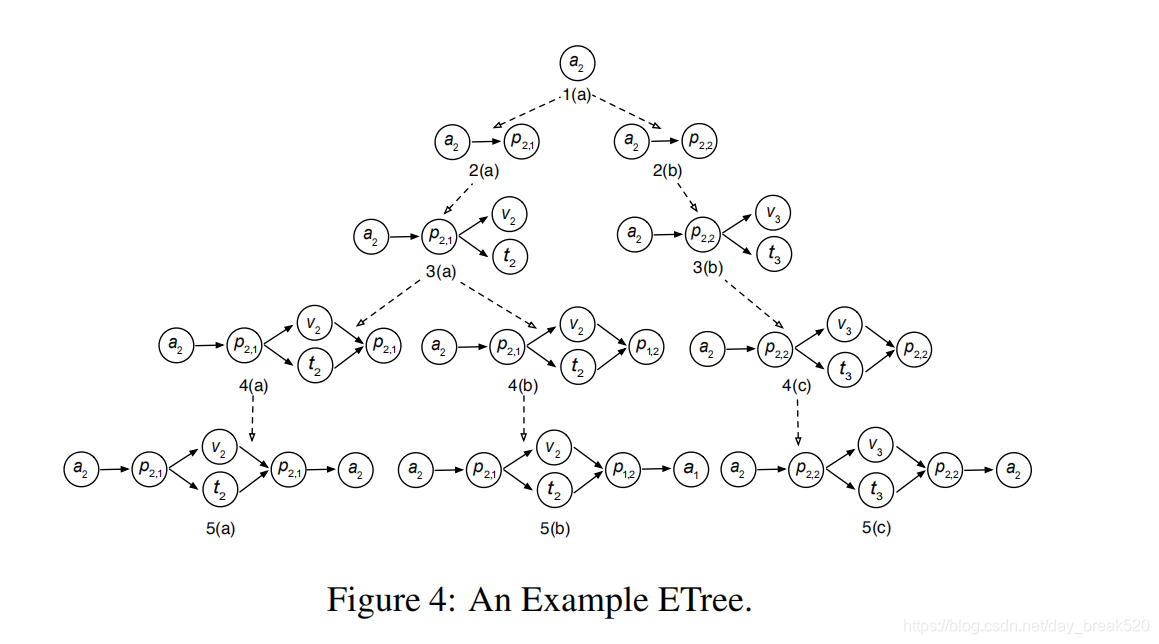
       在给出HIN、元结构S和起始节点os后，ETree是对HIN的子图展开过程进行跟踪形成的树形结构。下面给出论文给出的三种相似度计算方法。

定义3.StructCount.给出一个HIN G=(V,E)、一个元结构S=(N,M,ns,nt)、一个起始节点os和一个目标节点ot。StructCount模型的值就是以os作为起始节点、ot作为目标节点的元结构实例的数量。

        StructCount比较简洁方便使用，但是StructCount的值无法限制，度数越高的对象具有较大的StructCount值。当我们的目标是寻找最流行的对象时，这可能很有用，但是当我们关注对象的相关性时，这显然不合适。

定义4.Structure Constrained Subgraph Expansion(SCSE).给出一个HIN G=(V,E)、一个元结构S=(N,M,ns,nt)、一个起始节点os和一个目标节点ot，令ETree定义中函数w()的公式中α=1，我们可以给出相似度计算公式，其中S是元结构实例：

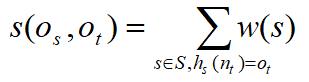
可以看到SCSE的根本思想是对由起始节点os能够延展到目标节点ot的元结构实例的概率进行建模。

定义4.Biased Structure Constrained Subgraph Expansion(BSCSE).给出一个HIN G=(V,E)、一个元结构S=(N,M,ns,nt)、一个起始节点os和一个目标节点ot，令ETree定义中函数w()的公式中α∈[0,1]。我们可以给出相似度计算公式，其中s是元结构实例:

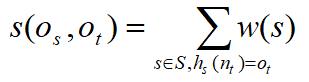
        BSCSE是StructCount和SCSE的集合模型，注意到，这里我们加入了α∈[0,1]参数，α是一个用来平衡StructCount和ASCSE的偏差因子。α越大，BSCSE越接近SCSE；α越小，BSCSE越接近StructCount。

原文链接