智能反射面增强星地安全传输

智能反射面使能的星地一体化网络安全协同传输

摘要

本文提出了一种由智能反射面（IRS）赋能的星地一体化网络安全协同传输策略。在该类网络中，于卫星用户附近部署智能反射面，用于反射地面网络产生的同频友好干扰，以保护卫星下行链路传输免遭窃听。我们旨在最小化为保证地面网络用户可靠通信以及限制卫星用户可容忍的最大干扰所对应的窃听者处的目标信噪比（SINR）。为此，设计了一种交替优化方案。仿真结果表明，所提出的基于智能反射面的协同干扰方案可显著降低窃听者处的目标信干噪比，从而实现显著的保密增益。

索引词

卫星通信，安全，协作，智能反射面，干扰。

一、引言

将卫星与地面网络相融合可以实现全球覆盖并扩展网络容量，为快速增长的物联网（IoT）应用[1]提供了至关重要的支持。此外，这种网络融合符合正在发展的第五代（5G）以及即将到来的6G通信网络[2],[3]的发展目标。然而，由于无线通信的开放性以及较大的波束覆盖范围，卫星下行链路通信容易受到窃听。此外，由于卫星通信系统与地面网络复用相同的频段，干扰问题也变得更加严重。近年来智能反射面（IRS）技术的发展，为应对安全和干扰问题提供了极好的机遇。

作为一种集成了大量反射单元的低成本平面表面结构，智能反射面（IRS）能够通过协调每个单元的反射系数[4]来智能地重构入射信号的传播特性。该特性常用于实现被动波束成形。结合发射天线处的主动波束成形，可在接收机处实现信号增强或抑制。目前，智能反射面辅助的通信系统已初步应用于提升频谱和能量效率[5]。例如，Zhang等[6]研究了实际中有限相移对数据传输速率的影响。进一步地，Di等[7]研究了在主动发射天线与被动智能反射面联合进行连续数字与离散波束成形设计下的和速率最大化问题。当无法获得完整的信道状态信息（CSI）时，已有研究为智能反射面辅助的多输入单输出（MISO）通信系统提出了鲁棒波束成形方案[8],[9]。在物理层安全（PLS）方面，智能反射面致力于在目的地有利地增强信号接收，同时在窃听者处破坏性地降低信号质量。已有若干波束成形方案或算法被研究用于保障特定场景下智能反射面辅助传输的安全性，包括单用户[10],[11]和多用户[12]下行链路窃听信道。Yu等[12]研究了在存在智能反射面的情况下，人工噪声（AN）辅助的波束成形方案，以实现系统和速率最大化，同时确保被潜在窃听者获取的信息量低于给定阈值。Wang等[13]提出了一种窃听者信道状态信息未知情况下的智能反射面辅助安全传输方案。在[13],中，在保证合法用户所需信号质量的前提下，最小化敏感信号功率，从而将更多发射功率分配给人工噪声以干扰窃听者。迄今为止，将智能反射面应用于星地一体化网络以实现干扰管理和安全的相关研究尚未开展。

本文研究了智能反射面（IRS）辅助的星地一体化网络中的安全传输优化问题。为了实现绿色且安全的通信，利用地面基站（BS）的信号作为友好干扰源来保护卫星下行通信，同时部署并利用智能反射面（IRS）以增强地面网络用户的信号、抑制对卫星用户的干扰，并恶化窃听者的接收性能。本文的主要贡献在于：1）首次在星地一体化网络中部署智能反射面（IRS）以提升系统安全性；2）提出了联合波束成形与干扰优化设计以增强安全性的方案。仿真结果表明，与无智能反射面（IRS）的传统协同干扰方案相比，所提出的由智能反射面（IRS）赋能的协同干扰方案显著降低了窃听者处的目标信号干扰噪声比（SINR），从而实现了更大的保密增益。

II. 系统模型与优化问题

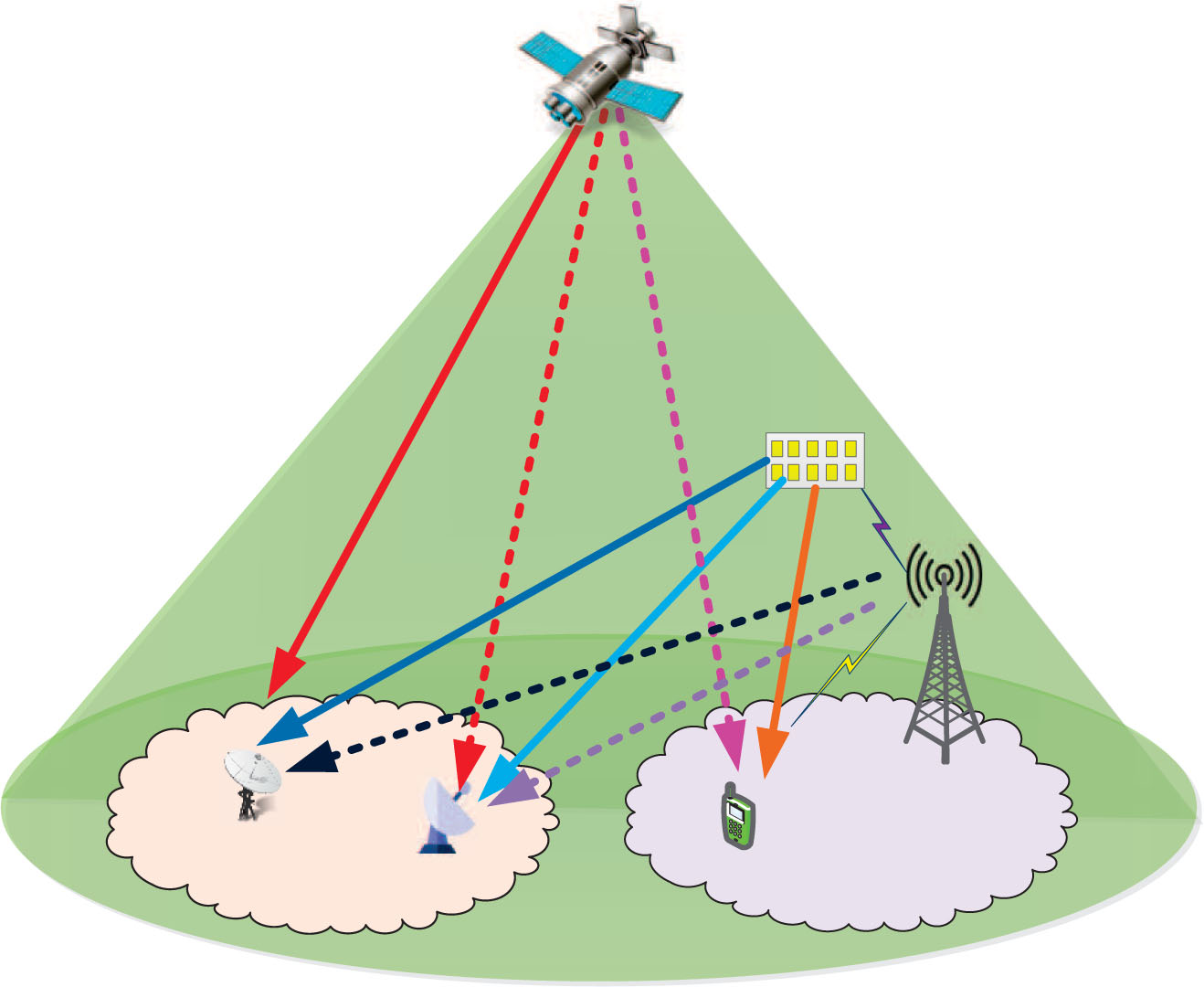
图1展示了星地一体化网络中由智能反射面（IRS）辅助的卫星下行通信，其中主网络（PN）与次网络（SN）共用相同的无线频谱资源，部署的智能反射面通过反射来自地面基站的有益干扰，以抑制窃听者（Eve）的信息截获。在主用户（PU）场景中，配备单一天线的卫星（SAT）向一个单天线主用户（PU）发送敏感信息，同时在PU附近的单天线窃听者（Eve）试图在同一波束中截获并解码卫星信息。与此同时，该N‐天线卫星网络（SN）中的基站（BS）为简化起见与单天线地面用户（SU）通信。此外，协作的基站靠近主用户（PU）和窃听者（Eve）。在发射功率预算的约束下，卫星（SAT）采用一种传输方案，旨在最大化主用户（PU）处接收信号的功率，而无需考虑限制窃听者（Eve）处的信号强度。通过协作，基站产生的绿色干扰被用于保障安全的卫星下行通信。

A. 信道模型

在此模型中，星地一体化网络中的所有链路均被假定为准静态慢衰落。令 $ h_p \in \mathbb{C} $、$ h_e \in \mathbb{C} $、$ h_s \in \mathbb{C} $、$ g_s \in \mathbb{C}^{N\times1} $、$ g_p \in \mathbb{C}^{N\times1} $、$ g_e \in \mathbb{C}^{N\times1} $、$ G_i \in \mathbb{C}^{L\times N} $、$ f_p \in \mathbb{C}^{L\times1} $、$ f_e \in \mathbb{C}^{L\times1} $ 和 $ f_s \in \mathbb{C}^{L\times1} $ 分别表示卫星‐主用户链路、卫星‐窃听者链路、卫星‐次用户链路、基站‐次用户链路、基站‐主用户链路、基站‐窃听者链路、基站‐智能反射面链路、智能反射面‐主用户链路、智能反射面‐窃听者链路和智能反射面‐次用户链路。假设 $ h_p / h_s $ 对主用户/次用户完全已知。$ g_s $、$ g_p $、$ g_e $ 和 $ G_i $ 在基站处完全已知，而 $ f_p $、$ f_e $ 和 $ f_s $ 的完整信息可由智能反射面获取。此外，假设卫星与基站独立运行。智能反射面上的反射单元数量为 $ L $，每个单元可分别将来自基站的信号反射至主用户和窃听者以实现安全传输，以及反射至次用户以增强信号接收。

在本文中，我们采用考虑大气效应的传统阴影莱斯衰落模型来描述卫星信道。具体而言，卫星信道模型由[14]给出
$$
h = CL\sqrt{b(\phi)}\tilde{h},
$$
其中 $ CL = \lambda/(4\pi\sqrt{d_0^2 + d_h^2}) $ 表示自由空间路径损耗系数，对应卫星高度为 $ d_0= 300 $ km，以及卫星覆盖区域中心与中心波束之间的距离为 $ d_h $。卫星‐用户信道的衰落系数为
$$
\tilde{h} = A\exp(j\psi) + Z\exp(j\phi).
$$
第一项 $ A\exp(j\psi) $ 表示散射分量，第二项 $ Z\exp(j\phi) $ 表示视距（LOS）分量。它们各自的平稳随机相位和确定性相位分别用 $ \psi \in[0, \pi] $ 和 $ \phi \in[0, \pi] $ 表示。第一项的幅度 $ A $ 服从瑞利分布，而第二项的幅度 $ Z $ 服从Nakagami‐$ m $ 分布。波束增益因子由
$$
b(\phi) = b_{\text{max}}\left( \frac{J_1(u)}{2u} + \frac{36J_3(u)}{u^3} \right)^2,
$$
with
$$
u = 2.07123 \frac{\sin\phi}{\sin(\phi_{3\,\text{dB}})},
$$
其中 $ b(\phi) $ 是用户位置的函数。$ b_{\text{max}} $ 表示卫星天线增益最大值。$ \phi_{3\,\text{dB}} $ 对应3 dB波束角，$ \phi $ 表示从SAT到用户和波束中心的两条视距路径之间的夹角。$ J_1(\cdot) $ 是一阶第一类贝塞尔函数，$ J_3(\cdot) $ 是三阶第一类贝塞尔函数。

本文仅考虑来自智能反射面的第一次反射信号，因为路径损耗较强。因此，主用户、窃听者和次用户接收到的信号分别为
$$
y_p = \sqrt{P_p}h_px_p + (g_p^H + f_p^H \Theta G_i) w x_s + n_p,
$$
$$
y_e = \sqrt{P_p}h_ex_p + (g_e^H + f_e^H \Theta G_i) w x_s + n_e,
$$
$$
y_s = \sqrt{P_p}h_sx_p + (g_s^H + f_s^H \Theta G_i) w x_s + n_s,
$$
其中，波束成形器 $ w \in \mathbb{C}^{N\times1} $ 用于发送信号 $ x_s $。 $ \Theta = \text{diag}(\beta_1e^{j\theta_1}, \beta_2e^{j\theta_2},…, \beta_L e^{j\theta_L}) $ 表示智能反射面的反射系数矩阵，包含第 $ l $ 个单元的相位偏移 $ \theta_l \in [0, 2\pi] $ 和幅度 $ \beta_l \in [0, 1] $ ($ l \in L={1, 2,…, L} $)。 $ n_p $、$ n_e $ 和 $ n_s $ 分别为主用户、窃听者和次用户的高斯白噪声，其分布分别为 $ n_p \sim \mathcal{CN}(0, \sigma_p^2) $、$ n_e \sim \mathcal{CN}(0, \sigma_e^2) $ 和 $ n_s \sim \mathcal{CN}(0, \sigma_s^2) $。噪声方差满足 $ \sigma_p^2 = \sigma_e^2 = \sigma_s^2 = \kappa T B $。$ \kappa \approx 1.38 \times 10^{-23} $ J/K 为玻尔兹曼常数，$ B $ 和 $ T $ 分别为噪声带宽和温度。需要注意的是，由于智能反射面的朝向，卫星信号经智能反射面反射后的功率被忽略。

然后，主用户、窃听者和次用户的信干噪比分别为
$$
\text{SINR}_p = \frac{P_p |h_p|^2}{\sigma_p^2 + |k_p^H w|^2}, \quad (1)
$$
$$
\text{SINR}_e = \frac{P_p |h_e|^2}{\sigma_e^2 + |k_e^H w|^2}, \quad (2)
$$
$$
\text{SINR}_s = \frac{|k_s^H w|^2}{\sigma_s^2 + P_p |h_s|^2}, \quad (3)
$$
其中 $ P_p $ 是卫星的功率预算。 $ k_p^H = g_p^H + f_p^H \Theta G_i $，$ k_e^H = g_e^H + f_e^H \Theta G_i $ 和 $ k_s^H = g_s^H + f_s^H \Theta G_i $。

B. 优化问题

定义 $ \theta = [\beta_1e^{j\theta_1}, \beta_2e^{j\theta_2},…, \beta_L e^{j\theta_L}] $。本文旨在在满足主用户和次用户的信干噪比约束条件下，最小化窃听者的信干噪比目标，该问题可表述为
$$
\min_{\theta,w} \text{SINR}_e, \quad (4a)
$$
$$
\text{s.t. } \text{SINR}_p \geq \gamma_p, \quad (4b)
$$
$$
\text{SINR}_s \geq \gamma_s, \quad (4c)
$$
$$
\text{Tr}(ww^H) \leq P_s, \quad (4d)
$$
$$
0 \leq \beta_l \leq 1, \quad 0 \leq \theta_l \leq 2\pi, \quad \forall l \in L, \quad (4e)
$$
其中 $ \gamma_s $ 是实现可靠通信的次用户信干噪比门限，而 $ \gamma_p $ 是主用户可容忍干扰的信干噪比上限。 $ P_s $ 是基站的功率预算。

III. 交替优化

尽管约束条件 (4d) 是凸的，但由于约束条件 (4b) 和 (4c) 涉及反射系数向量 $ \theta $ 和发射波束成形 $ w $ 的耦合，导致问题(4)难以求解。鉴于问题(4)不易直接求解，我们考虑交替优化 $ \theta $ 和 $ w $ 来寻找其解。本文提出通过交替优化两个子问题来求解：1) 在固定 $ \theta $ 时优化 $ w $

III. 交替优化（续）

和 2) 在固定 $ w $ 的情况下优化 $ \theta $。然后给出了整体算法、收敛性以及计算复杂度。

A. 子问题I：在固定 $ \theta $ 的情况下优化 $ w $

为了解决非凸问题(4)，采用半定松弛(SDR)方法将问题提升到更高维度。定义 $ W \triangleq ww^H $。对于任意给定的 $ \theta $，非凸问题(4)可被重新表述为
$$
\min_W \text{SINR} e, \quad (5a)
$$
$$
\text{s.t. } \text{SINR}_p \geq \gamma_p, \quad (5b)
$$
$$
\text{SINR}_s \geq \gamma_s, \quad (5c)
$$
$$
W \succeq 0, \quad \text{Tr}(W) \leq P_s, \quad (5d)
$$
$$
\text{rank}(W) = 1. \quad (5e)
$$
将(1)、(2)和(3)代入该问题，并忽略秩约束 $ \text{rank}(W) = 1 $，我们得到
$$
\min_W \frac{P_p |h_e|^2}{\sigma_e^2 + k_e^H W k_e}, \quad (6a)
$$
$$
\text{s.t. } \frac{P_p |h_p|^2}{\sigma_p^2 + k_p^H W k_p} \geq \gamma_p, \quad (6b)
$$
$$
\frac{k_s^H W k_s}{\sigma_s^2 + P_p |h_s|^2} \geq \gamma_s, \quad (6c)
$$
$$
W \succeq 0, \quad \text{Tr}(W) \leq P_s. \quad (6d)
$$
引入辅助变量 $ \tau > 0 $，并考虑到 $ P_p |h_e|^2 $、$ P_p |h_p|^2 $、$ P_p |h_s|^2 $ 与 $ w $ 无关，该问题被重新表述为
$$
\max {W} \tau, \quad (7a)
$$
$$
\text{s.t. } k_e^H W k_e \geq \tau, \quad \tau > 0, \quad (7b)
$$
$$
k_p^H W k_p \leq \frac{P_p |h_p|^2}{\gamma_p} - \sigma_p^2, \quad (7c)
$$
$$
k_s^H W k_s \geq \gamma_s (\sigma_s^2 + P_p |h_s|^2), \quad (7d)
$$
$$
W \succeq 0, \quad \text{Tr}(W) \leq P_s. \quad (7e)
$$
显然，(7) 是一个凸问题。

B. 子问题II：在固定 $ W $ 的情况下优化 $ \theta $

对于任意给定的 $ w $，非凸问题(4)可以被重新表述为
$$
\min_\theta \text{SINR} e, \quad (8a)
$$
$$
\text{s.t. } \text{SINR}_p \geq \gamma_p, \quad (8b)
$$
$$
\text{SINR}_s \geq \gamma_s, \quad (8c)
$$
$$
0 \leq \beta_l \leq 1, \quad 0 \leq \theta_l \leq 2\pi, \quad \forall l \in L. \quad (8d)
$$
该问题被进一步重写为
$$
\max \theta \tau, \quad (9a)
$$
$$
\text{s.t. } |k_e^H w|^2 \geq \tau, \quad \tau > 0, \quad (9b)
$$
$$
|k_p^H w|^2 \leq \frac{P_p |h_p|^2}{\gamma_p} - \sigma_p^2, \quad (9c)
$$
$$
|k_s^H w|^2 \geq \gamma_s (\sigma_s^2 + P_p |h_s|^2), \quad (9d)
$$
$$
0 \leq \beta_l \leq 1, \quad 0 \leq \theta_l \leq 2\pi, \quad \forall l \in L. \quad (9e)
$$
设 $ v = \theta^H $，其中 $ v_l = \beta_l e^{j\theta_l}, \forall l \in L $。则约束(9e)可等价地写为模一约束： $ |v_l|^2 \leq 1, \forall l \in L $。令 $ f_e^H \Theta G_i = v^H \Phi_e $，其中 $ \Phi_e = \text{diag}(f_e^H) G_i $，约束(9b)可重写为
$$
|k_e^H w|^2 = (g_e^H + v^H \Phi_e) w w^H (g_e^H + v^H \Phi_e)^H, \quad (10a)
$$
$$
= v^H \Phi_e w w^H \Phi_e^H v + v^H \Phi_e w w^H g_e + g_e^H w w^H \Phi_e^H v + g_e^H w w^H g_e. \quad (10b)
$$
非凸约束(10b) 可以等价地写为
$$
|k_e^H w|^2 = \bar{v}^H R_e \bar{v} + g_e^H w w^H g_e,
$$
其中
$$
R_e = \begin{bmatrix}
\Phi_e w w^H \Phi_e^H & \Phi_e w w^H g_e \
g_e^H w w^H \Phi_e^H & 0
\end{bmatrix}, \quad \bar{v} = \begin{bmatrix} v \ t \end{bmatrix},
$$
其中 $ t $ 表示一个松弛变量。注意 $ \bar{v}^H R_e \bar{v} = \text{Tr}(R_e \bar{v} \bar{v}^H) $。

令 $ V = \bar{v} \bar{v}^H $，其中 $ V \succeq 0, \text{rank}(V)=1 $。约束(9b)被重写为
$$
\text{Tr}(R_e V) + g_e^H w w^H g_e \geq \tau. \quad (11)
$$
类似地，约束(9c)和(9d)可以重写为
$$
\text{Tr}(R_p V) + g_p^H w w^H g_p \leq \frac{P_p |h_p|^2}{\gamma_p} - \sigma_p^2, \quad (12)
$$
$$
\text{Tr}(R_s V) + g_s^H w w^H g_s \geq \gamma_s (\sigma_s^2 + P_p |h_s|^2), \quad (13)
$$
其中，矩阵 $ R_p $ 和 $ R_s $ 与 $ R_e $ 具有相似的含义。不难发现，(11)∼(13)等价于(7c)∼(7d)。另一方面，约束(9e)等价于 $ V_{l,l} \leq 1 $（$ V_{l,l} $ 表示矩阵 $ V $ 的 $ (l, l) $-单元）， $ \forall l \in L $。此外，$ V_{L+1,L+1} = 1 $。

通过采用SDR技术并去除约束 $ \text{rank}(V)= 1 $，问题(9)可重写为
$$
\max_V \tau, \quad (14a)
$$
$$
\text{s.t. (11)∼(13) satisfied,} \quad (14b)
$$
$$
V_{l,l} \leq 1, \quad l \in L, \quad (14c)
$$
$$
V_{L+1,L+1} = 1, \quad (14d)
$$
$$
V \succeq 0. \quad (14e)
$$
由于半定规划(SDP)问题(14)必须是凸的，许多现有的凸优化求解器都能高效地求解它。

备注 ：通常情况下，松弛问题(7)和(14)可能不具备秩一特性。换句话说，$ W $ 和 $ V $ 的秩不等于一。为了处理被省略的秩约束，需要恢复一个可行的秩一解。具体而言，如果复厄米特矩阵 $ W^ $ 和 $ V^ $ 为秩一，则可通过奇异值分解实现恢复；否则，可采用标准高斯随机化方法[15]来恢复问题(4)的一个秩一近似解 $ w^ $ 和 $ v^ $（对应于 $ \bar{v}^* $）。

C. 整体算法

算法1给出了问题(4)的整体算法，其中 $ \text{SINR}_e^{(k)} $ 表示在第 $ k $ 次迭代中，变量 $ w^{(k)} $ 和 $ v^{(k)} $（对应于 $ \Theta^{(k)} $）下问题(4)的目标值，

算法1： 问题(4)的所提算法。

1: 初始化：设置 $ k= 0 $，$ w^{(0)}= g_s/|g_s| $，
$ \bar{v}^{(0)} = [1, 1,…, 1]^H $ 和 $ \text{SINR}_e^{(0)} = \frac{P_p |h_e|}{1 + |k_e^{(0)H} w^{(0)}|^2} $。

2: 重复

3: 设置 $ k= k+ 1 $。

4: 在给定 $ \bar{v}^{(k-1)} $ 的情况下，求解问题 (7)，然后恢复一个近似解 $ w^{(k)} $。

5: 在给定 $ w^{(k)} $ 的情况下，求解问题 (14)，然后恢复一个近似解 $ \bar{v}^{(k)} $，后跟 $ \theta^{(k)} $。

6: 设置 $ \text{SINR}_e^{(k)} = \frac{P_p |h_e|}{1 + |k_e^{(k)H} w^{(k)}|^2} $。

7: 直到 $ \frac{\text{SINR}_e^{(k)} - \text{SINR}_e^{(k-1)}}{\text{SINR}_e^{(k)}} < \varepsilon $。

$ \varepsilon > 0 $ 是一个小的阈值。算法1必须收敛，因为两个子问题在迭代过程中均为非递增，且问题(4)的最优值有下界。此外，根据我们的仿真，大多数情况下这两个子问题的迭代次数 $ T $ 小于10，目标精度为 $ \varepsilon = 10^{-3} $。对于子问题I，凸问题(7)包含1个大小为 $ N $ 的复数值线性矩阵不等式(LMI)约束和5个实值标量LMI约束。因此，内点法(IPM)可以高效求解该问题。给定 $ \varepsilon_1 $，求解(7)的 $ \varepsilon_1 $-最优解所需的迭代次数数量级为 $ C_1 = \ln(1/\varepsilon_1) \cdot \sqrt{2N + 5} $。每次迭代的总计算代价数量级为 $ C_2 = 8n_1N^3 + 4n_1^2N^2 + 5n_1^2 + 5n_1 $，其中 $ n_1 = O(4N^2) $。对于子问题2，凸问题(14)包含1个大小为 $ L $ 的复数值LMI约束和 $ L + 5 $ 个实值标量LMI约束。类似地，IPM也能高效求解该问题。给定 $ \varepsilon_2 $，求解(14)的 $ \varepsilon_2 $-最优解所需的迭代次数数量级为 $ C_3 = \ln(1/\varepsilon_2) \cdot \sqrt{3L + 8} $。每次迭代的总计算代价数量级为
$ C_4 = 8n_2(L+5)^3 + 4n_2^2(L+5)^2 + n_2^2(L+6) + n_2(L+6) $，其中 $ n_2 = O(4(L+1)^2) $。因此，算法1的复杂度由以下给出
$$
C = T[(C_1 \times C_2) + (C_3 \times C_4)]
= T[\ln(1/\varepsilon_1)\cdot\sqrt{2N+5}(8n_1N^3 + 4n_1^2N^2 + 5n_1^2 + 5n_1) + \ln(1/\varepsilon_2)\cdot\sqrt{3L+8}(8n_2(L+5)^3 + 4n_2^2(L+5)^2 + n_2^2(L+6) + n_2(L+6))].
$$

IV. 数值结果

本节将通过数值仿真来评估所提出的智能反射面辅助的协同干扰设计所实现的性能。作为对比，还给出了无智能反射面辅助的传统协同干扰方案作为对照，如[14]所示。假设卫星链路经历服从参数为 $ (b_i, m_i, \Omega_i) = (0.063, 2, 8.97 \times 10^{-4}) \; \forall i \in {p, e, s} $ 的阴影莱斯衰落和严重阴影效应。此外，其他信道在小尺度上服从瑞利衰落分布，其路径损耗由 $ PL = -42 -10\rho \log_{10}(d/d_0) $ dB 给出，其中 $ \rho $ 表示路径损耗指数。另外，由于信号仅由智能反射面的前半球反射，因此可合理假设每个单元具有3 dBi增益。其他一些仿真参数设置如下：卫星的发射功率为 $ P_p = 1 $ W；载波频率为 $ \lambda = 20 $ GHz；卫星的最大天线增益为 $ b_{\text{max}} = 52 $ dBi；卫星/主用户/窃听者与次用户之间的波束角度均设为 $ 0.01^\circ $；3 dB波束角为 $ \phi_{3\,\text{dB}} = 0.4^\circ $；噪声温度 $ T = 300 $ K 以及噪声带宽 $ B = 50 $ MHz；BS-SU、BS-PU、BS-Eve、BS-IRS 和 IRS-SU 链路的路径损耗指数和距离分别设置为 $ \rho_{bs} = \rho_{bp} = \rho_{be} = \rho_{bi} = \rho_{is} = 1 $，$ d_{be} = 85 $ m，$ d_{bs} = 80 $ m，$ d_{bp} = 85 $ m，$ d_{bi} = 80 $ m，$ d_{is} = 76 $ m。IRS-PU、IRS-Eve 链路的路径损耗指数和距离分别设置为 $ \rho_{ip} = \rho_{ie} = 1.2 $ 或 $ 1.5 $，$ d_{ip} = d_{ie} = 8 $ m 或 $ 12 $ 米。次用户实现可靠通信的最小SINR门限设置为 $ \gamma_s = 0.8 \times \text{SINR} {s0} $，主用户的最大可容忍干扰SINR约束设置为 $ \gamma_p = 0.5 \times \text{SINR} {p0} $，其中 $ \text{SINR} {s0} $ 和 $ \text{SINR} {p0} $ 表示在无智能反射面的非合作方案中，波束成形器设计为与从基站到次用户的信道对齐时，次用户和主用户处达到的信干噪比。所有仿真曲线均基于200次随机观测的平均结果绘制。

A. 信噪比 $ \text{SINR}_e $ 与 $ L $ 的关系

图2展示了在 $ N = 8 $ 情况下，窃听者的信干噪比目标 $ \text{SINR}_e $ 与智能反射面的反射单元数量 $ L $ 之间的关系，其中基站的发射功率设置为 $ P_s = 3 $ dBW。与没有智能反射面的传统协作干扰方案相比，所提出的智能反射面辅助协作干扰方案具有更低的 $ \text{SINR}_e $。该结果证实了智能反射面在提升保密性方面的有效性。从图2还可以观察到，$ \text{SINR}_e $ 在很大程度上依赖于 $ L $。随着 $ L $ 的增加，所提出的智能反射面辅助协作干扰方案中的 $ \text{SINR}_e $ 单调增加。原因非常明显：更多的反射单元意味着可以向主用户和窃听者转发更多的有益干扰功率。通过自适应地控制每个单元的幅度和相位状态，实现了保密性能增益。另一方面，智能反射面-主用户/窃听者链路的路径损耗指数以及距离也显著影响 $ \text{SINR}_e $。

B. 信噪比 $ \text{SINR}_e $ 与 $ P_s $ 的关系

图3展示了在 $ N = 8 $ 或 $ 4 $ 两种情况下，窃听者的信干噪比目标 $ \text{SINR}_e $ 与地面基站发射功率 $ P_s $ 之间的关系，其中智能反射面的反射单元数量设为 $ L = 100 $。我们可以观察到，对于所有曲线，随着 $ P_s $ 的增加，$ \text{SINR}_e $ 单调且持续下降。其原因是基站的发射功率越高，对窃听者造成的干扰越强。我们还发现，$ N $ 对 $ \text{SINR}_e $ 有影响。当基站配备更多的发射天线时，尽管空间自由度增加，$ \text{SINR}_e $ 并不一定随之降低。这主要是因为 $ \gamma_p $ 和 $ \gamma_s $ 的设置与发射天线数量相关。因此，更多的发射天线会导致 $ \gamma_p $ 和 $ \gamma_s $ 的不同设置值。根据仿真结果可以明显看出，所提出的智能反射面辅助协作干扰方案相较于传统方案具有更低的 $ \text{SINR}_e $。此外，当使用智能反射面时，$ P_s $ 的增加对保密增益的贡献更大。

结论

本文提出了一种在地面基站和智能反射面（IRS）处实现的、面向卫星‐地面一体化网络的安全协作干扰设计，旨在增强卫星下行通信的安全性。为了在满足次用户可靠通信和主用户最大可容忍干扰的条件下，最小化窃听者的信干噪比目标，提出了一种用于联合波束成形的交替优化算法。仿真结果表明，与无IRS的传统协同干扰方案相比，所提方案显著降低了窃听者的信干噪比目标。此外，随着IRS反射单元数量和地面基站发射功率的增加，以及IRS到主用户和窃听者之间的路径损耗和距离的减小，所提方案实现的保密增益也随之提高。