UHMWPE的疲劳与断裂性能

36 超高分子量聚乙烯的疲劳与断裂

36.1 引言

近年来，超高分子量聚乙烯（UHMWPE）的力学性能引起了广泛关注[1–12]。抗疲劳裂纹扩展和断裂强度是用于指导第一代和第二代高交联超高分子量聚乙烯配方开发的重要性能指标[2,13–19]。UHMWPE材料的疲劳与断裂性能的临床意义取决于具体的假体装置。在回收的髋臼衬垫中通常以磨粒性和粘着性磨损机制为主，而在取出的胫骨垫片中则常观察到疲劳损伤表面[2,20]。因此，耐磨性在髋臼部件中具有首要重要性，而膝关节典型的较低匹配度和较高接触应力使得疲劳和断裂性能更为相关[16]。然而，最近已有报道显示髋臼部件出现裂纹以及髋臼衬垫边缘发生断裂的情况[21–23]，通常与非关节面区域的异常载荷或撞击有关[21]。此外，如果UHMWPE配方未得到适当稳定，体内氧化可能改变其初始性能[24–25]，长期来看可能影响假体组件的磨损和力学性能。因此可以得出结论：医用级UHMWPE配方应在设计考虑、耐磨性、氧化稳定性以及疲劳和断裂性能之间取得平衡[18–19,26]。

第一代和第二代高交联度超高分子量聚乙烯的开发推动了大量关于这些材料以及常规超高分子量聚乙烯的疲劳与断裂性能的研究，但在研究理念和实验方法上存在差异。高交联超高分子量聚乙烯的特性已在第6、15–19及25章中进行了详细总结，如果本章中涉及这些材料的术语对读者而言较为陌生，可参考前述章节。本章的目的旨在提供有关疲劳和断裂概念的理论背景，以及针对超高分子量聚乙烯（UHMWPE）的不同哲学方法和实验技术。同时概述了当前医用超高分子量聚乙烯在疲劳和断裂性能方面的主要研究成果。

36.2 疲劳抗力

36.2.1 疲劳抗力基本概念

苏雷什的经典定义指出，当材料受到循环加载时，疲劳是发生的渐进性和局部性结构损伤[27]。相应地，疲劳寿命被定义为达到所研究材料灾难性失效所需的循环次数。从结构角度来看，疲劳损伤的进展会引发微观结构变化，进而导致微观裂纹的形核。随后，微观裂纹不断扩展并合并，形成一条主导性的宏观裂纹，该裂纹以稳定的方式扩展，直至发生结构失稳或完全断裂。因此，特定材料或构件的疲劳寿命包含五个阶段，即通过微观结构变化产生永久损伤、微观裂纹萌生、微观缺陷扩展与合并形成主导裂纹、主导裂纹的稳定扩展以及最终断裂[27]。因此，总寿命是由与临界疲劳裂纹萌生和扩展相关的各种事件组合而成。基于这些定义，分析材料疲劳强度可采用两种主要哲学方法：全寿命方法和缺陷容限方法。全寿命方法旨在预测构件的服役寿命，其假设初始材料和实验室试样无缺陷，即无裂纹或无缺陷，并将疲劳寿命随应力变化的实验数据与预测的服役条件。相比之下，缺陷容限方法假定零部件和实验室试样在某种程度上均存在缺陷，至少包含检测方法无法检出的最大尺寸缺陷。在这种情况下，萌生时间被忽略，因为假定裂纹萌生已经发生或无关紧要。因此，缺陷容限方法仅关注假定缺陷的扩展，或通过设计防止其扩展。此外，缺陷容限方法比全寿命方法更为保守，因为它假定不存在萌生时间，而通常情况下材料中产生连贯缺陷需要一定的时间。因此，缺陷容限方法预测的缺陷从初始尺寸扩展至失效所需的时间是一个下限估计值。该方法利用断裂力学和疲劳裂纹扩展（FCP）实验与分析来预测零部件中缺陷的行为，而传统的全寿命疲劳分析则主要依赖应力分析。

36.2.2 疲劳分析：全寿命方法

为了预测部件在疲劳条件下的总寿命，通常会对无缺口的、名义上光滑的部件材料试样进行简单实验，记录失效时间（或载荷循环次数）与施加应力之间的函数关系。通过应力分析，可将实验数据转换为部件中的预测应力，从而估算部件的服役寿命。实验室试样的失效时间被称为总寿命，因为它从一个假设为无缺陷的初始状态开始，其中部分寿命用于产生可合并成连贯缺陷的损伤，其余寿命则用于使该缺陷扩展直至部件失效。疲劳实验试样通常承受循环载荷或应变，其波形由用户自定义，从最小应力σmin到最大应力σmax，或从最小应变εmin到最大应变εmax。因此，根据测试过程中控制的参数不同，总寿命实验可分为应力控制的或应变控制的。描述一个应力控制的总寿命疲劳试验通常给出多个参数，即应力范围∆σ= σmax − σmin、应力幅值σa = 1/2(σmax − σmin)、平均应力σm、应力比R = σmin/σmax、频率ν、失效循环次数Nf以及波形（如正弦、三角）[9]。对于应变控制的总疲劳寿命，也定义了类似的参数实验。传统上，当失效发生在少于1000个循环次数内的全疲劳寿命实验被称为低周疲劳，实验室试样通常在塑性范围内经历循环应变。相反，在高周疲劳实验中占主导的是循环弹性应变。

材料（基于应力）疲劳强度的表征采用所谓的应力‐寿命，即S–Nf图（图36.1），其中S代表应力幅值，Nf代表在半对数坐标下达到失效（或某种临界状态）的循环次数。S–Nf图描述了在递减的应力幅值下达到失效所需的循环次数，其数学表达式为巴兹金关系式：S= A Nf^B。在S–Nf图中，导致无失效（在一千万次循环后仍存活，或“无限寿命”）的最高应力水平称为疲劳极限[9]。

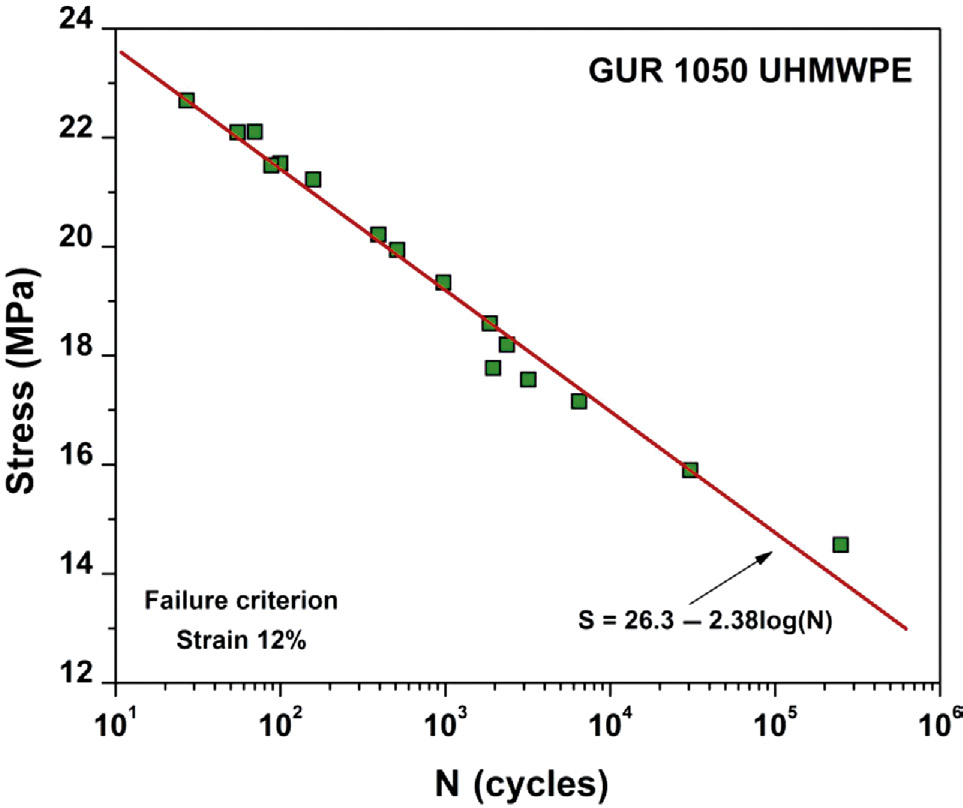
36.2.3 超高分子量聚乙烯的总寿命-疲劳测试

与金属不同[27,28]，关于聚合物（包括超高分子量聚乙烯）疲劳缺陷形核的问题仍缺乏深入理解。然而，威廉姆斯和德弗里斯[29]通过监测非晶态聚合物样品在循环载荷下自由电子数量的变化，证实了缺陷的形核过程，并发现材料中断裂键的数量持续增加，且与载荷波形一致。因此，在实验的每个载荷循环中，聚合物中的化学键都会发生断裂，从而导致损伤随着时间的推移而累积，提供了损伤累积和缺陷形核的机制。然而，超高分子量聚乙烯（UHMWPE）的全疲劳寿命实验的主要局限性在于，这些实验几乎从未在低于其抗拉强度（UTS）的情况下导致试样实际断裂，即使在显著的循环塑性应变条件下也是如此[30]。这可能导致一个错误的结论，即如果一个UHMWPE部件没有缺陷，它就不会发生疲劳失效。相反，已经观察到裂纹在超高分子量聚乙烯部件的缺口和应力集中处萌生并扩展[31–34]。因此，对超高分子量聚乙烯中疲劳裂纹的形成与扩展的研究主要从缺陷容限观点出发，迄今为止，报道UHMWPE达到灾难性失效的总寿命测试的研究仍十分匮乏[12,35–37]。此外，仅有一项研究以传统的高周疲劳方式进行[38]。

总寿命研究在加载条件、试样形状、温度和环境方面可能存在差异。虽然韦特曼和莱特采用了旋转弯曲疲劳装置，但比利亚拉加等人[12,36]的研究代表了小冲孔技术的一种改进，用于评估各种超高分子量聚乙烯材料在双轴加载条件下直至断裂的总寿命。另一方面，奥康纳等人研制了一种多站弯曲疲劳试验机，通过对传统和温辐照绝热熔融（WIAM）交联超高分子量聚乙烯试样进行弯曲加载，实现两千万次循环的疲劳测试。尽管本研究中循环次数很高，WIAM交联试样仍未发生失效[35]。最近，奥拉尔等人设计了一种悬臂柱弯曲试验，以证实老化维生素E掺杂辐照超高分子量聚乙烯相比老化传统超高分子量聚乙烯具有更好的弯曲疲劳抗力[39]。由于总疲劳寿命测试需要极长的实验时间，设备故障非常频繁，普鲁伊特及其同事[40]以及普埃尔托拉斯及其同事[8,41,42]采用了一种替代标准（而非完全断裂）来提前终止疲劳试验。他们认为当超高分子量聚乙烯达到临界量的塑性变形（∼12%）时，微损伤已经开始，因为已有基于超小角X射线散射评估的微观疲劳损伤证据[43]。采用上述标准，贝克等人发现，经连续再熔和退火过程处理后的γ‐辐照超高分子量聚乙烯的屈服寿命（即应变达到12%之前的循环次数）均低于原始材料，唯独在最高辐照剂量（200 kGy）下辐照的材料例外[40]。这种在最高辐射剂量下保持屈服寿命的原因被归因于非晶区的强化，尽管辐照和热处理的各自影响尚未完全区分清楚。另一方面，根据乌里耶斯等人[41]的研究，随着辐照剂量增加，电子束辐照且未经热稳定化的超高分子量聚乙烯表现出比原始材料更长的屈服寿命。

同一研究组后续的研究[8,42]发现，辐照后退火和再熔融处理对辐照态超高分子量聚乙烯的屈服寿命有害，再熔融使屈服寿命降至原始材料水平以下，无论辐照剂量如何。辐照态材料屈服寿命的提高与辐照引起的片晶厚度增加相关，而退火和再熔融导致的屈服寿命下降则与片晶厚度减小有关。该研究组最近的一项工作还报道了辐照后退火和顺序交联的超高分子量聚乙烯具有类似的屈服寿命行为[44]。

尽管上述屈服寿命结果表明在疲劳情况下对非弹性应变累积具有相对的抗力，但不应将其与真实的总寿命数据互换使用。在持续循环加载下应变的累积可能更能反映材料的抗蠕变性，而抗蠕变性确实与其疲劳和断裂抗力相关，如第36.2.6.1节所述。因此，该指标（屈服寿命结果）与静态或循环加载条件下最终失效之间确切的一一对应关系仍有待证实。索比拉杰等人在研究五种临床相关的超高分子量聚乙烯配方在应力集中情况下的单调与疲劳行为时，已在一定程度上探讨了这一问题[37]。因此，他们并未使用光滑试样，而是测试了带有两种缺口几何形状（中等和深缺口）的圆柱形哑铃状试样。作为应力升高的缺口的存在显著改变了单轴单调测试的情况，因为它诱发了三轴应力状态，导致所谓的缺口强化（更高的轴向屈服应力）、取向硬化的降低以及在缺口表面发生断裂萌生[45,46]。本研究的临床相关性显而易见，因为大多数超高分子量聚乙烯部件设计都包含应力升高特征，例如沟槽、圆角或凹槽。

尽管采用了以试样断裂定义为失效的全寿命方法，这些研究人员仍将超过250,000次循环未发生断裂的寿命视为无失效。无失效数据并未被舍弃，而是被纳入最大似然估计（MLE）对S–Nf行为的分析。主要发现是，索比拉杰等人报告指出，尽管与传统材料相比，交联超高分子量聚乙烯配方的失效分布具有更高的方差，但在缺口条件下的疲劳行为有所改善（图36.2）。这一行为通常与上述屈服寿命研究的结果一致[47,48]。

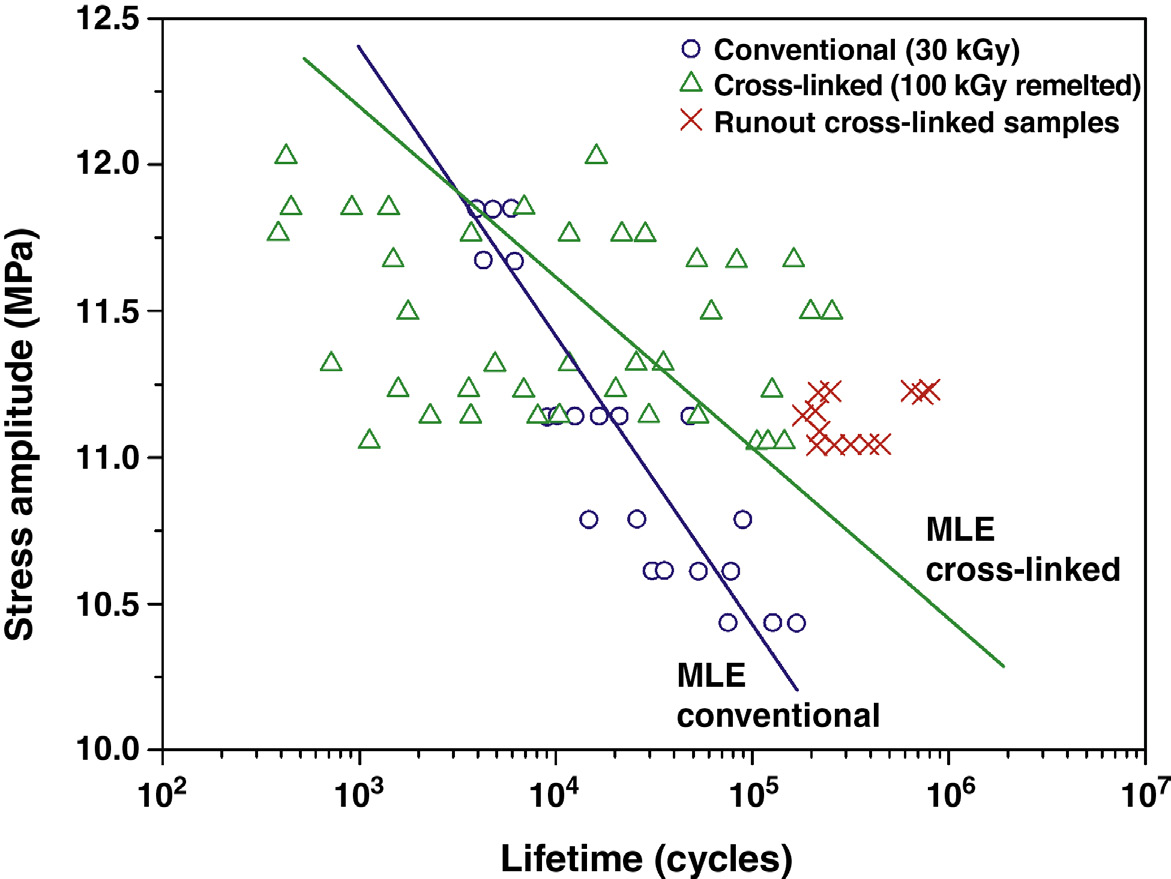
总之，在过去的20年中，研究人员已经生成了大量关于现代医用超高分子量聚乙烯配方的全寿命疲劳数据。然而，全寿命方法固有的实验复杂性使得研究人员选择了不同的、在某些情况下相悖的策略，限制了不同机构之间结果的可比性。在这方面，实验室间的合作计划以及对现有全寿命数据的荟萃分析，例如帕斯夸尔等人[49]的研究，可能对推动超高分子量聚乙烯疲劳失效领域的发展具有重要意义。

36.2.4 疲劳分析：缺陷容限法

36.2.4.1 线弹性断裂力学（LEFM）

缺陷容限方法假设材料或结构部件本质上存在缺陷，如前所述。在这种情况下，疲劳寿命基于初始裂纹或缺口的扩展，在循环加载作用下增长至临界尺寸[9,50,51]。通常采用线弹性断裂力学来研究疲劳裂纹扩展现象。线弹性断裂力学假设材料在移动裂纹尖端附近的区域以纯弹性方式变形，并提供了一个简单的框架，其中用一个参数——应力强度因子K，即可充分描述应力和应变环境。缺点是，在移动裂纹尖端所发生的严苛条件下，没有任何材料会以完全弹性的方式行为。然而，对于广泛的问题和材料本征行为而言，线弹性断裂力学能够充分描述疲劳裂纹扩展和断裂过程中的应力和应变环境。

在线弹性断裂力学（LEFM）中，无论加载模式或裂纹几何形状如何，当距离裂纹尖端的距离r趋近于零时，尖锐裂纹尖端附近的应力以1/√r的幂次增加。根据加载条件的不同，存在三种疲劳裂纹扩展（FCP）模式：I型为张开模式（施加应力垂直于裂纹面和裂纹前沿），II型为剪切模式，其位移为平行于裂纹面且垂直于裂纹前沿的剪切类型，III型为扭转模式，其位移为平行于裂纹面和裂纹前沿的剪切。I型应力强度因子K可定义为：

$$ K_{I} = \lim_{r \to 0} \sqrt{2\pi r} \sigma_{ij}^{I}(\theta) $$

其中局部应力场σij取决于应力强度因子K以及函数fij(I)，该函数描述了相对于裂纹面角度θ的与模式相关的应力分布。

K与裂纹长度a、系统几何形状（通过几何修正系数Y）以及作用在裂纹上的远场载荷σ∞唯一相关：

$$ K_{I} = \sigma_{\infty} Y \sqrt{\pi a} $$

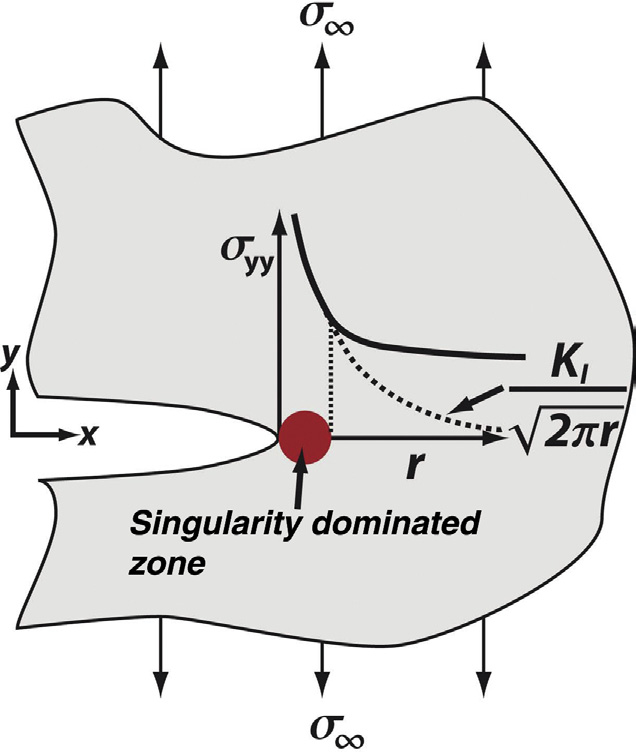
图36.3示意性地描绘了I型应力强度因子及其与局部和全局应力的关系。张开模式通常最重要的，因此也是被研究最多的。在裂纹尖端附近，K及方程36.1和36.2适用的区域称为奇异性主导区。只要在奇异性主导区内非线性、塑性或时间相关效应可以忽略，则线弹性断裂力学（LEFM）是量化裂纹尖端状况的极好方法。否则，必须用其他方法对LEFM进行补充或替代。

36.2.4.2 疲劳裂纹扩展基础

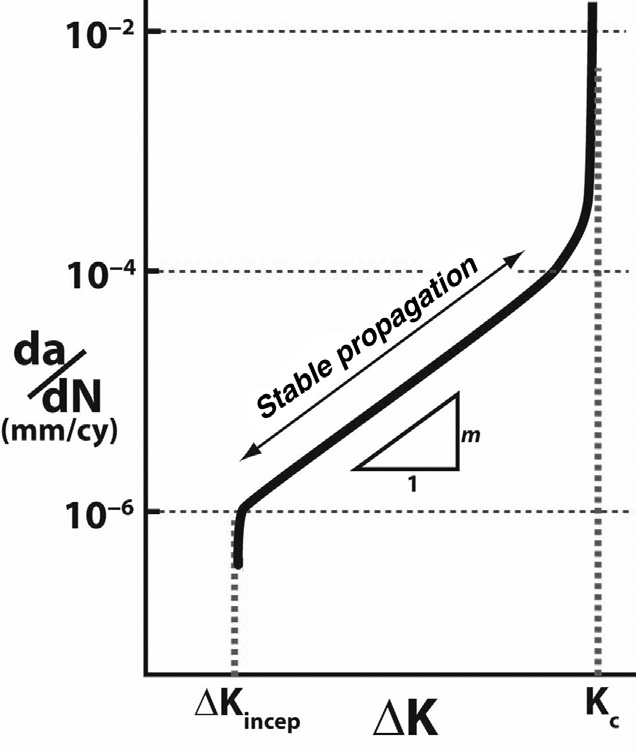
从经验角度来看，疲劳裂纹扩展（FCP）可分为三个阶段：第I阶段，此时无明显扩展，裂纹基本处于非活跃状态；稳定扩展即第II阶段；以及不稳定扩展即第III阶段。（图36.4）。第II阶段的起始点或阈值（约在10⁻⁶毫米/周期）由裂纹萌生时的应力强度因子∆Kincep给出，该值是驱动裂纹扩展所需的最小应力强度因子范围；而Kc是不稳定裂纹扩展和快速断裂的临界应力强度因子。在第II阶段，许多工程材料在循环加载条件下稳定裂纹扩展速率遵循帕里斯方程：

$$ \frac{da}{dN} = C (\Delta K)^m = C (K_{\text{max}} - K_{\text{min}})^m $$

其中a为裂纹长度，N表示载荷循环次数，∆K为应力强度因子范围，C和m为作为材料属性处理的经验拟合参数。需要注意的是，在恒定循环应力作用下扩展的裂纹会经历逐渐增大的应力强度因子，最终达到临界状态并发生断裂。

36.2.5 超高分子量聚乙烯中的疲劳裂纹扩展测试

疲劳裂纹扩展（FCP）实验在标准断裂试样上进行，例如带缺口的紧凑型拉伸试样，通常使用伺服液压加载框架。测试前，先用剃刀片将缺口尖端修锐，然后进行疲劳预开裂，以获得尽可能尖锐的初始裂纹。初始裂纹形成后，施加具有固定应力比R的载荷波形，通过光学显微镜技术监测试样和裂纹扩展。与总寿命疲劳方法一样，温度效应在超高分子量聚乙烯的裂纹扩展实验中也具有重要意义，因为其在体温下的疲劳抗力明显低于室温下的疲劳抗力[3]。有关疲劳裂纹扩展试样和实验的完整描述可参见ASTM E647‐13ae1[52]。

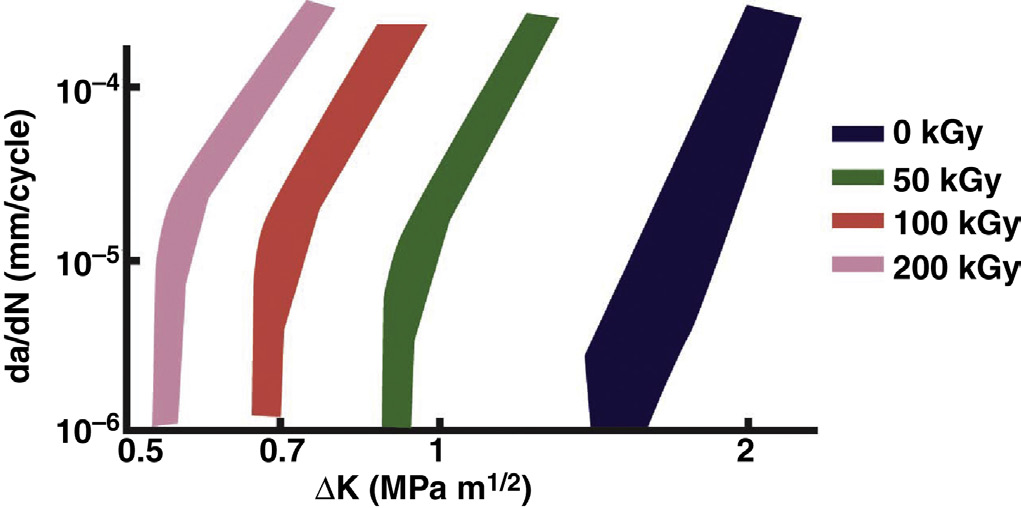
关于常规和高交联超高分子量聚乙烯的疲劳裂纹扩展研究已证实，随着辐射交联水平的提高，其抗裂纹萌生和裂纹扩展能力受到不利影响[5,40,42,53–55]。图36.5包含了贝克等人提供的数据散点条带，表明随着辐射剂量的增加，疲劳裂纹扩展性能持续下降[40]。多项研究表明，辐照后重熔会进一步降低疲劳裂纹扩展性能。一方面，由于交联密度较高导致塑性变形能力降低，被认为是辐照态高交联超高分子量聚乙烯疲劳裂纹扩展性能下降的主要原因；另一方面，辐照后重熔引起的结晶度下降显然也部分解释了高交联超高分子量聚乙烯疲劳裂纹扩展行为的进一步恶化。已有研究证明，对于辐照后退火的高交联超高分子量聚乙烯、高结晶性和高交联的超高分子量聚乙烯以及高压结晶的含维生素E的超高分子量聚乙烯，结晶性的提高对该性能具有积极影响[5,8,54,56]。对于逐次交联超高分子量聚乙烯，研究人员报告其疲劳裂纹扩展行为与辐照后退火的超高分子量聚乙烯基本相同，这与其相似的结晶性相符[44]。阿特伍德等人的最新研究进一步证实了辐射剂量的主导作用（即交联密度）和结晶性特征（结晶度百分比和片晶尺寸）对多种临床相关超高分子量聚乙烯材料的疲劳裂纹扩展行为的影响[26]，包括未处理对照组、单次或多剂量γ射线辐照后热处理的材料。此外，这些研究人员已证实疲劳裂纹扩展抗力、耐磨性和氧化性能之间存在权衡关系，这对超高分子量聚乙烯部件的长期成功可能至关重要，在开发替代型超高分子量聚乙烯材料时应审慎考虑。例如，奥拉尔等人通过设计一种表面交联超高分子量聚乙烯解决了上述权衡问题，该材料由维生素E稳定化，表面具有高交联密度以提高耐磨性，而本体具有低交联密度以实现高的疲劳裂纹扩展抗力[57]。

36.2.6 粘弹性疲劳裂纹扩展

36.2.6.1 粘弹性裂纹扩展模型及疲劳裂纹扩展现象的预测

沙佩里、萨克塞纳、威廉姆斯等人开展的研究详细分析了在蠕变和应变率相关材料中的裂纹行为，并为超高分子量聚乙烯（UHMWPE）中疲劳裂纹扩展（FCP）表现出的脆性本质提供了预测依据[58–63]。其中，沙佩里和威廉姆斯所建立的模型尤为有用，这些模型将材料内在的本构粘弹性松弛行为与稳定裂纹尖端的扩展直接关联起来[61,63]。这些模型的优势在于其力学预测能力，能够将FCP动力学与材料易于通过简单的一维蠕变试验测得的粘弹性行为联系起来。该模型的基本推论可解释UHMWPE中观察到的静态模式疲劳裂纹扩展行为，从而可能为该材料的疲劳与断裂行为提供基于第一性原理的解释。

继威廉姆斯的研究之后[63]，我们考虑一种根据简单幂律（大于时间t= 0）均匀松弛的粘弹性固体：

$$ C(t) = C_0 \left( \frac{t}{\tau_0} \right)^d $$

其中C为材料的柔量系数，τ₀为时间常数，d为松弛幂律指数，E₀为瞬时（t = 0）弹性模量。对于恒定载荷（P =为常数），其解为

J积分，表示材料断裂韧性的度量（参见第36.3.4节关于断裂抗力），其表达式为：

$$ J(t) = J_0 \left( \frac{t}{\tau_0} \right)^d $$

其中J₀是t= 0时静态解的J积分值。显然，J值以与柔度相同的速率持续增加。这意味着，如果载荷持续施加（以静态或循环方式），最终将超过裂纹扩展阈值Jc，从而导致断裂不可避免。该关于超高分子量聚乙烯结构中裂纹萌生的预测尚未得到验证，但它可能有助于解释最近报道的在交联超高分子量聚乙烯髋关节轴承中应力集中处萌生断裂的现象[22,31,33]。

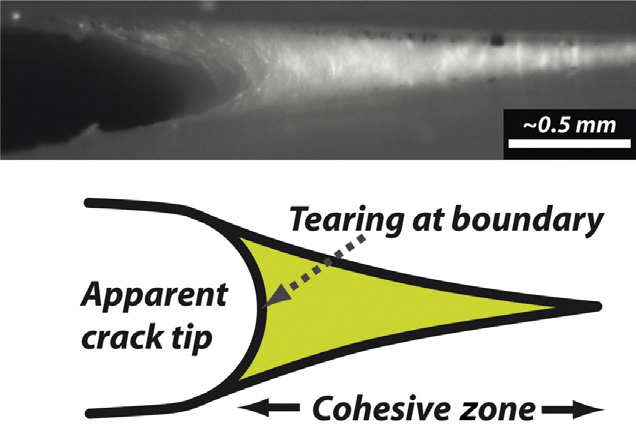
由上述可知，裂纹前沿附近粘塑性材料（即粘聚区）的变形和失效主导了超高分子量聚乙烯中材料对裂纹扩展的抗力（参见图36.6）。因此，粘聚区材料的抗蠕变性应在裂纹扩展中起主导作用[64]。很少有研究分析大应变下超高分子量聚乙烯的蠕变行为，而在此情况下这显然具有重要意义[65]。这些文献表明，对于由高度应变的屈服后材料组成的粘聚区而言，小应变蠕变实验可能与其行为无关，因为在大应变下蠕变速率显著降低。因此，高度应变的块体超高分子量聚乙烯的蠕变和松弛行为值得更多关注，这有助于更好地从机理上理解动态加载条件下裂纹的扩展。

36.2.6.2 循环与静态模式行为的疲劳裂纹扩展关系

帕里斯方程描述了在已知由于循环模式现象而产生裂纹的材料中稳定裂纹扩展速率（公式36.3）。另一方面，静态或蠕变模式下的裂纹扩展可用以下方程描述：

$$ \frac{da}{dt} = A (K(t))^n $$

这类似于帕里斯方程，只是该过程取决于瞬时应力强度因子K，而不是其波动或循环分量[66]。这种情况可称为静态模式裂纹扩展，因为该过程对循环现象本身不敏感per se。以这种方式行为的材料中稳定的裂纹扩展也大致与施加的循环应力强度的最大值相关，即

$$ \frac{da}{dN} = B K_{\text{max}}^q $$

公式36.7通常与帕里斯方程不一致。考虑裂纹扩展的静态和循环模式组分的一个基本方法是将两个过程进行叠加[67]：

$$ \frac{da}{dN} = \left[ \frac{\partial a}{\partial N} \right] {t} + \frac{1}{f} \left[ \frac{\partial a}{\partial t} \right] {N} $$

其中每个带括号的微分项都保持未微分参数固定。因此，在公式36.8中，裂纹扩展是仅对加载和卸载事件敏感的一个分量与另一个不受循环影响但反映时间（静态模式）效应的分量之和。这些带括号的表达式对应于公式36.3和36.6，并可重写为（其中f= dN/dt）：

$$ \frac{da}{dN} = \left[ \frac{da}{dN} \right] {\text{fatigue}} + \frac{1}{f} \left[ \frac{da}{dt} \right] {\text{creep}} $$

其中材料可能对所谓的疲劳（循环损伤）或蠕变（静态模式；与循环无关）的总裂纹扩展分量更为敏感，该方程表示了这一点在疲劳裂纹扩展中，蠕变的贡献实际上被考虑在内。这种形式主义简单地叠加了每种机制的影响，从而排除了静态和循环模式疲劳裂纹扩展结合时的协同效应。

36.2.6.3 超高分子量聚乙烯的静态模式疲劳裂纹扩展

静态模式下的裂纹扩展并不普遍称为疲劳过程。里奇仅将循环过程特别关联到疲劳[68]，而聚合物中裂纹的静态模式扩展通常被称为慢速裂纹扩展[69–72]。但需要注意的是，尽管在静态加载条件下不会发生循环模式扩展，但静态模式裂纹扩展却会在循环加载条件下发生。

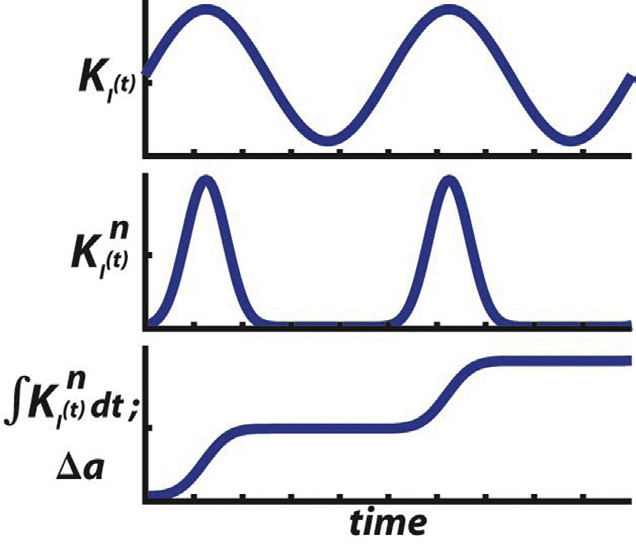
考虑一个正弦载荷控制试验及其相关的应力强度因子K，如图36.7顶部所示。然后通过计算公式36.6得到裂纹扩展速率da/dt（见图36.7中间图，其中n= 8）。如果对公式36.6进行时间积分，则可得到给定时间段内的总裂纹扩展量，如图36.7底部所示。由此可见，只要裂纹扩展处于稳定区域，在循环加载条件下就会发生增量式裂纹扩展。

在这些条件下，裂纹扩展的可预测性对循环加载情形有两个简单的推论。首先，对于给定的波形，循环次数应无关紧要，因为幂律的时间积分对频率不敏感。其次，对于具有相同应力范围和载荷比的不同波形（例如正弦和方波），疲劳裂纹扩展速率幂律的时间积分将不相同，因此某些波形会显得更有害于其他波形，且这种差异以数学上可预测的方式呈现。弗曼斯基和普鲁伊特在常规超高分子量聚乙烯中检验了静态模式疲劳裂纹扩展行为的这两个推论，以评估静态模式模型的适用程度[73]。

医用级GUR 1050柱塞挤出UHM-WPE，未辐照，被加工成紧凑型拉伸试样。在伺服液压加载架上进行了两个实验，以测试该材料中FCP的静态模式特性。在第一个实验中，分别对不同的试样施加两种正弦载荷控制波形，载荷比R = 0.1。以1 Hz或0.1 Hz的正弦波形持续加载33.4分钟，在每次测试之间取出试样，并使用光学显微镜记录裂纹扩展情况。因此，实验的持续时间T以及幂律的时间积分保持不变，而循环次数和频率则有所变化。第二个实验采用了与第一个实验相同的试样，比较了在1 Hz下相同持续时间内方波和正弦波形的影响。在这种情况下，测试持续时间、循环次数和频率保持不变，而FCP幂律的时间积分则有所不同。

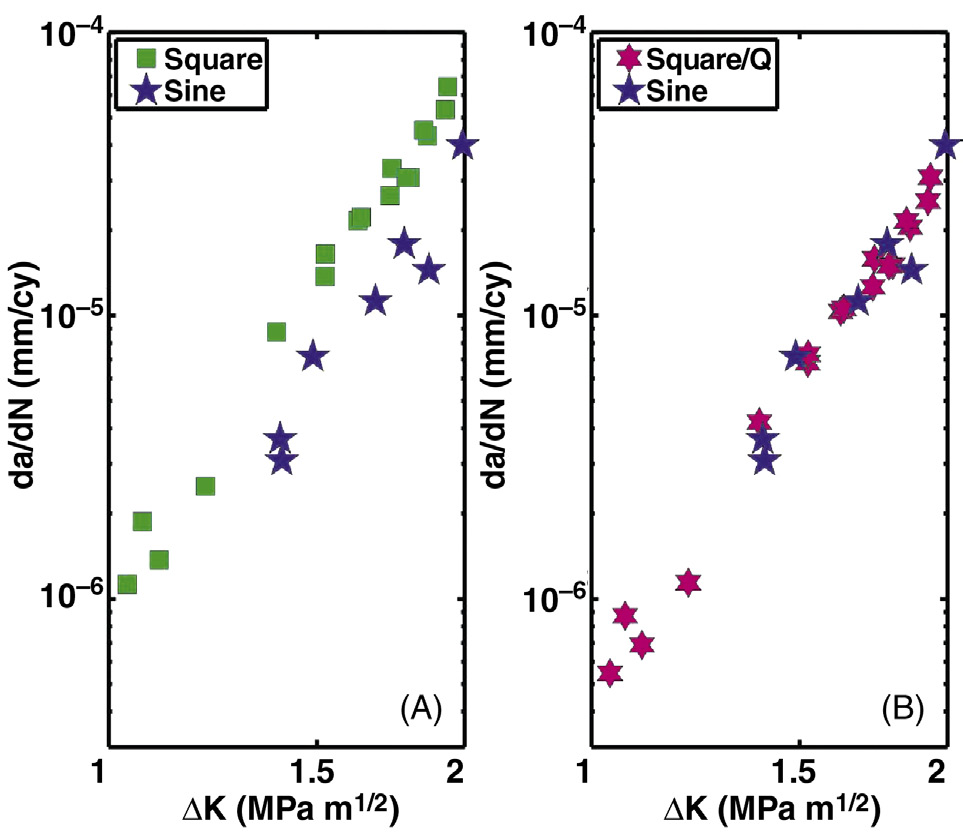
频率效应的结果表明，裂纹扩展每循环在0.1 Hz测试中大约高出一个数量级，这对于静态模式FCP是预期之内的，因为1 Hz测试的循环次数多出10倍（图36.8A）。然而，

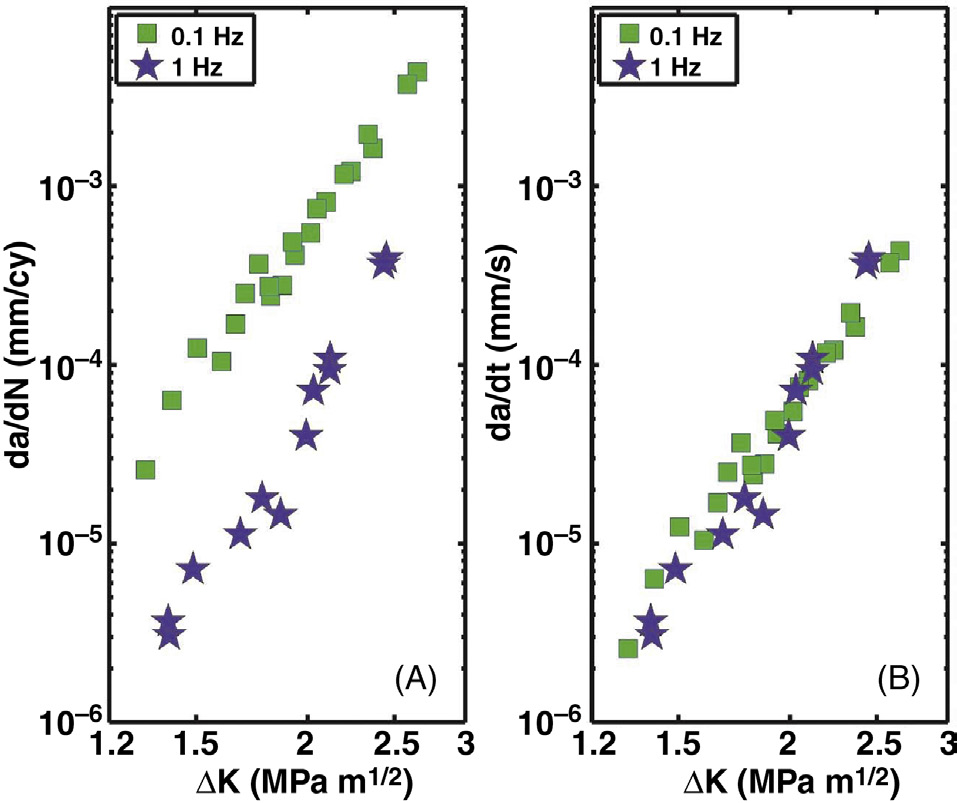
当裂纹扩展以单位时间为基准作图时，数据发生坍塌（图36.8B），表明疲劳裂纹扩展过程从根本上取决于持续时间，而非循环次数。

方波波形的裂纹扩展速率始终高于正弦波波形，且高出一个恒定倍数因子（图36.9A）。因此，稳定裂纹扩展区在对数‐对数坐标轴上呈平行分布。这种因子是静态模式FCP所预期的结果，从公式36.10可以看出，FCP幂律的积分在方波波形下大于正弦波波形。该乘性因子Q仅仅是持续时间为公式36.10期间实验所预测的裂纹扩展之比：

$$ Q = \frac{\int_{0}^{\lambda} (K_{\text{square}})^n dt}{\int_{0}^{\lambda} (K_{\text{sin}})^n dt} \approx 2.1 $$

当方波波形数据通过Q进行归一化后，所有数据坍缩为一组（图36.9B）。仅使用疲劳裂纹扩展速率幂律指数和方程36.6对静态模式裂纹扩展速率的预测，与实验观察到的裂纹扩展速度差异表现出极好的一致性方波和正弦波形。综合结果表明，在循环纯拉伸载荷条件下，传统超高分子量聚乙烯中的疲劳裂纹扩展以静态模式发生，且不会产生显著的循环模式损伤。

36.2.6.4 Kmax主导的超高分子量聚乙烯疲劳裂纹扩展

静态模式FCP的另一个显著特征是该过程与峰值应力强度因子（Kmax）相关，而不是与帕里斯方程中使用的∆K相关。弗曼斯基和普鲁伊特以及西里马米拉等人最近研究了不同R条件下对FCP的影响，并证明常规和交联超高分子量聚乙烯中的疲劳裂纹扩展与Kmax相关，而与∆K[50,74]无关（另见表36.1）。弗曼斯基和普鲁伊特最近已表明，Kmax依赖性（公式36.7）可直接由公式36.6[75]推导得出。

本研究进行了三项实验，每项实验采用不同的载荷范围序列。第一项实验采用固定载荷比R = 0.1。第二项实验同样采用固定载荷比R = 0.5，以评估平均应力增加对该材料疲劳裂纹扩展（FCP）的影响。第三项实验保持载荷Pmax恒定，探究变化载荷比的总体影响。

R = 0.1实验的结果显示，不仅存在显著的裂纹起始应力强度范围（图36.10），而且存在符合经典帕里斯方程（公式36.3）的稳定裂纹扩展区，其幂律指数m = 9.5。R= 0.5实验的数据也表明在整个测试范围内存在稳定的扩展区域，但没有亚临界裂纹扩展。这些数据显然表明叠加的额外静态平均应力与循环应力共同作用时会产生不利影响。图36.10中的黑色星形数据对应于固定Pmax（可变R）实验。在高应力强度范围（低R）下，Pmax在图36.10中的数据收敛至R= 0.1的数据。然而，在较低的应力强度范围，数据似乎趋近于一个恒定的裂纹扩展速率。所采用的低应力强度（高R）范围波形，在Pmax固定时，接近于一个稳态施加载荷Pmax，其中循环分量相对于载荷的静态分量可忽略不计。这些实验数据之间的差异表明，∆K并不是用于描述超高分子量聚乙烯中疲劳裂纹扩展的普遍适用的关联参数。

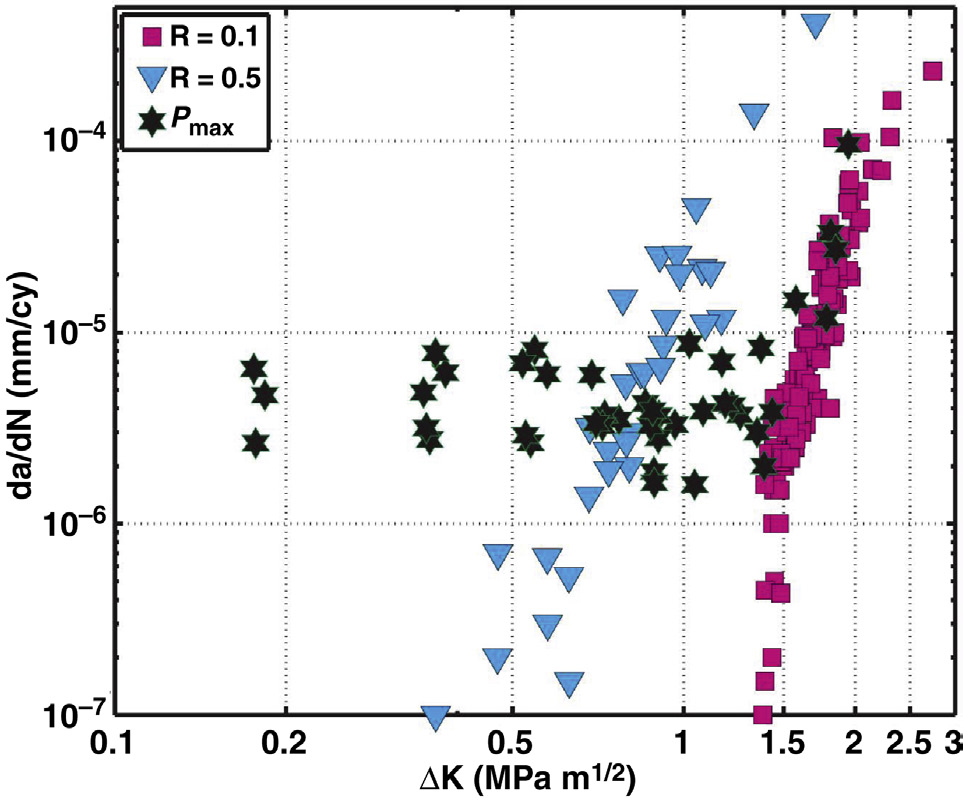
当使用Kmax作为FCP关联参数绘制图36.10中的实验数据时（图36.11），三项实验的稳定扩展结果均汇合到一条共同的趋势线上。这表明，对于传统超高分子量聚乙烯而言，起主导作用的FCP关联参数是Kmax，而不是∆K。该结果表明，在这些实验条件下，超高分子量聚乙烯中的稳定裂纹扩展可用公式36.7描述，且该材料中的裂纹可以在没有显著循环加载的情况下发生扩展。

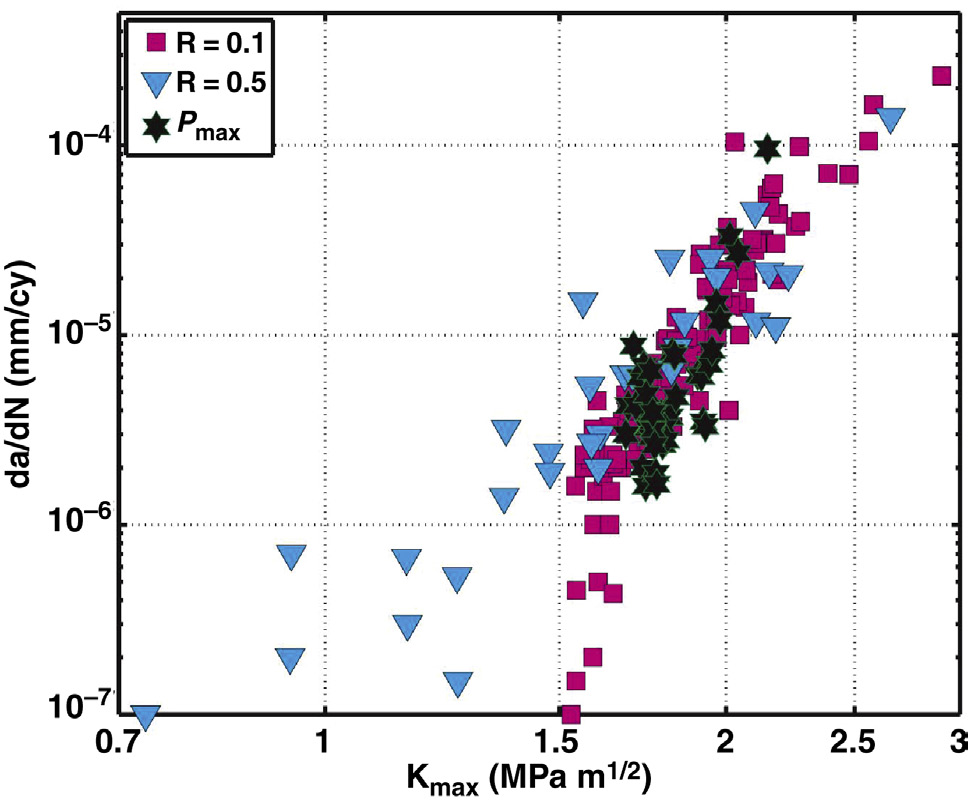
最后，我们观察到超高分子量聚乙烯中的裂纹扩展在静态模式下可靠发生，其韧性和疲劳裂纹扩展速率幂律指数符合经典脆性工程材料的预期。表36.1总结了以下两者之间的比较从疲劳裂纹扩展和断裂行为的角度来看，陶瓷、金属和超高分子量聚乙烯的比较表明，从断裂力学角度来看，超高分子量聚乙烯符合被视为本质上脆性材料的要求[68,76]，在设计和应用中应像对待其他脆性、损伤不可容忍的工程材料一样予以充分考虑。

	超高分子量聚乙烯	脆性	延性
关联参数	Kmax	Kmax	∆K
幂律指数	8–20	8–50	2–4
断裂韧性应力强度因子Kc (MPa√m)	0 kGy 4 100 kGy 3	SiC 3 Si 1	Ti‐6Al‐4V 65–100 4340钢 50–100

36.2.7 非传统的疲劳实验方法

除了传统的疲劳测试方法外，其他实验方法也被用于在机械上重现与全关节置换体临床使用中相似的疲劳条件。例如，我们在此介绍超高分子量聚乙烯文献中的两项研究，它们分别更精确地模拟了膝关节的环境以及人工髋关节和膝关节轴承的最差临床情况。

36.2.7.1 超高分子量聚乙烯和维生素E掺杂超高分子量聚乙烯中的滑动疲劳方法

富田等人开发了一种双向滑动疲劳试验，试图模拟更接近全膝关节超高分子量聚乙烯部件中所见条件的测试环境[77]。在此试验中，一个钛合金销（半球形半径为3毫米的尖端形状）沿着光滑的超高分子量聚乙烯样品以简单往复或U形路径滑动。试样浸没在37°C水中，施加载荷为196牛顿。滑动疲劳试验后，扫描声学断层成像技术可检测疲劳后的超高分子量聚乙烯试样中的次表面裂纹。富田研究组首次基于滑动疲劳结果认识到添加维生素E（0.1%）对抑制传统超高分子量聚乙烯中次表面裂纹形成及最终分层的积极作用[77]。在随后的研究中，同一作者报告了γ射线辐照的超高分子量聚乙烯试样在次表面晶界处出现裂纹萌生和扩展的有害加速现象，该现象进一步发展为表面粗糙度并最终导致试样分层[78]。同样，添加维生素E的压缩成型超高分子量聚乙烯的制造方法在防止次表面裂纹形成方面表现出有效性。

36.2.7.2 结构抗疲劳方法

王等人采用了一种结构疲劳实验方法，以评估由不同交联超高分子量聚乙烯制成的髋臼衬垫和胫骨垫片在接近最差临床情况下的疲劳性能[79]。薄型髋臼内衬（2.5毫米厚；32毫米直径）和骨水泥固定的髌骨组件分别在髋关节和髌股关节模拟器中进行测试。髋臼衬垫放置时，在内衬穹顶与金属壳之间留有4毫米间隙，使杯体在边缘异常支撑。施加同步生理载荷模式（150–2450牛顿）和交叉路径运动，持续100万次循环。使用钴铬股骨头和稀释小牛血清润滑。结构疲劳试验每25万次循环中断四次，以便检查边缘断裂并对未断裂的内衬进行磨损评估。同样，将髌骨组件与对齐良好和错位（内旋6度）的股骨部件配

36 超高分子量聚乙烯的疲劳与断裂

36.3 断裂抗力

36.3.1 引言

众所周知，由于超高分子量聚乙烯（UHMWPE）具有极高的分子量及其相应的微观结构，因此它是一种韧性高（抗断裂性很强）的聚合物。事实上，UHMWPE常被用作增韧剂，用于开发聚合物共混物[80–84]。由于UHMWPE是一种能量吸收能力强且高度延性的聚合物，全关节置换体中的UHMWPE部件磨损，特别是在全膝关节置换术（TKA）中，并非单纯由疲劳机理引起，而是由疲劳‐断裂联合作用过程导致的[7,85]。单轴拉伸试验、冲击实验以及基于断裂力学方法的多种测试手段已被用于表征聚合物的抗断裂性。特别是自20世纪80年代末以来，已开展了大量关于UHMWPE韧性比较与绝对估算的研究，以及针对制造工艺（如：压制成型、辐照和稳定化）引起该性能变化的表征研究。本节旨在总结前述各项技术的实验细节，并简要回顾其在各类医用级超高分子量聚乙烯（UHMWPE）表征中的应用。

36.3.2 单轴拉伸失效：断裂功和估算的KC

尽管单轴拉伸试验是最简单的实验方法之一，但它能够提供材料力学性能和特性的基本信息。在本实验中，将一个名义上光滑的哑铃形试样在恒定应变率下进行单轴变形直至失效（参见ASTM D638‐10）[86]。拉伸试验的结果通常以著名的应力（单位面积上的载荷）–应变曲线形式显示（见第6章和第39章），在分析超高分子量聚乙烯的大变形行为时，应正确转换为真实应力和应变。真实应力–应变曲线下的面积提供了使拉伸试样变形并最终断裂所需总应变能的估计值。试样断裂时的该应变能称为能量韧性，有时也称为断裂功，常被用作材料整体韧性的估算。然而必须强调的是，这并不是其断裂韧性的实际度量。例如，与工程合金相比，超高分子量聚乙烯具有较高的能量韧性，但其断裂韧性较低，且抗裂纹扩展能力较差。

当试样在拉伸实验中断裂时，失效通常起源于试样内部可识别的裂纹或缺陷。基于断口表面的观察和线弹性断裂力学（LEFM）的应用，可利用此结果估算材料的韧性。在材料断裂前，且满足平面应变条件时，应力强度因子达到一个临界值，该临界值被视为断裂韧性的度量，Kc：

$$ K_c = \sigma_u Y \sqrt{\pi \left( \frac{a}{W} \right)} $$

其中σu为极限真实应力。例如，图36.12A和B显示了中心表面存在初始微孔或缺陷的100 kGy电子束辐照UHMWPE拉伸试样的断口表面。对断口表面的详细观察发现，围绕初始缺陷存在所谓的稳定裂纹扩展区和快速断裂区。对于此特定情况，极限应力和断口表面特征给出了Kc值为1.7 MPa√m。该估算的Kc值与传统疲劳裂纹扩展分析得到的结果并不完全一致，但验证了极限应力与缺陷尺寸之间的趋势符合线弹性断裂力学的[4–5]。类似地，Gencur等人报道了原始状态、辐射灭菌以及辐照后稳定化的高交联度超高分子量聚乙烯的Kc结果。他们观察到退火和再熔融的高交联超高分子量聚乙烯的K值均有所降低（分别为2.8 ± 0.4和3.0 ± 0.6 MPa√m），相对于原始状态和辐射灭菌的UHMWPE（分别为4.0 ± 0.5和4.5 ± 1.1 MPa√m）而言，这归因于前者更高的交联密度[4]。

36.3.3 伊佐德和夏比冲击试验

尽管单轴拉伸试验可被视为对材料断裂抗力的一种准静态测量方法，但冲击试验代表了一种动态情景，其中实验室试样在更短的时间尺度内（远小于一秒）发生变形和断裂过程。经典的伊佐德和夏比试验是评估材料冲击强度最广泛使用的方法。在这两种试验中，摆锤以其臂端的重物向下摆动，撞击并通常使缺口试样断裂。试样断裂会吸收摆锤的部分能量，这一情况反映在撞击后摆锤达到的最大高度上。伊佐德与夏比试验的主要区别在于缺口试样的放置位置：前者为垂直放置，后者为水平放置。此外，在伊佐德试验中缺口朝向摆锤，而在夏比试验中则相反。有关伊佐德和夏比冲击试验的描述及其针对超高分子量聚乙烯（UHMWPE）的具体修改方法，可参见ASTM F648和ISO 5834[87]。缺口冲击试验中吸收的能量常被用来与断裂韧性或裂纹扩展速率测试（FCP tests）的结果进行比较，但二者之间的关联最多仅为定性。冲击试验涉及高塑性应变率以及不确定程度的动态裂纹扩展，这两者都会改变材料及裂纹尖端区的行为，因此在工程问题中应谨慎使用冲击性能数据。

必须指出，测试超高分子量聚乙烯需要使用双缺口伊佐德试样，因为单缺口试样无法实现完全断裂。用于生物医学植入物的超高分子量聚乙烯所需的最小冲击韧性强度根据超高分子量聚乙烯树脂的黏度而定（ASTM F648），范围为25 kJ/m²至126 kJ/m²（伊佐德法）或30 kJ/m²至180 kJ/m²（夏比法）。尽管根据ASTM F648，冲击强度是一项关键性能，但在骨科文献中关于现代医用超高分子量聚乙烯冲击强度的报道相对较少[8,88–93]。这些研究大多证实，随着辐照剂量的增加，超高分子量聚乙烯的冲击强度下降，当辐照剂量在110 kGy至255 kGy之间时，冲击强度下降幅度为35%至65%。胡奥特等人最近不仅证明了辐射剂量对多种重熔的高交联超高分子量聚乙烯冲击韧性具有显著降低作用，还发现冲击韧性与能量韧性测量值之间存在强相关性[92]。辐射剂量对冲击韧性的影响可能还会受到其他变量的影响，例如生产工艺、辐射类型、辐照温度或后续热处理。在这方面，格林等人报告称，在相同辐照剂量下，较低分子量的超高分子量聚乙烯树脂表现出明显更高的冲击强度，制造方法影响较小，并且在相同剂量下，电子束辐照试样的韧性高于伽马射线辐照的试样[88]。研究人员报告了辐照后退火和顺序交联的超高分子量聚乙烯具有相似的冲击韧性[44,94]。最近，傅等人提出了一种改进塑性和韧性的新型超高分子量聚乙烯，其工艺为先进行后固结高温熔融[90]，然后进行辐射交联[91]。这些研究背后的原理是，高温熔融将增强超高分子量聚乙烯链的扩散，从而最大限度地减少结构缺陷，并同时提高韧性。因此，经压缩成型的超高分子量聚乙烯的双缺口伊佐德冲击韧性在280摄氏度下高温熔融12小时后从127 kJ/m²增至175 kJ/m²。此外，辐射交联导致的典型韧性损失被辐照前高温熔融所获得的改善冲击韧性所补偿[91]。

总体而言，上述研究表明，传统超高分子量聚乙烯承受高能冲击的能力随着辐照剂量的增加（即交联密度的增加）而逐渐降低。未辐照和150 kGy辐照超高分子量聚乙烯冲击试样的断口表面所呈现的特征也支持这一结论（见图36.13A和B）。注意原始聚合物中存在具有显著变形迹象的条带（或条纹）（图36.13C和D），而辐照并重熔状态下的试样则表现为光滑断口表面。在这方面，Puértolas等人最近将冲击超高分子量聚乙烯试样断口表面表现出的断口形貌特征与仪器化冲击试验机提供的载荷‐挠度曲线中不连续性的存在（或缺失）相关联[93]。因此，特定冲击试样吸收的能量似乎与其断口表面上条纹的数量和尺寸有关。这种有条纹的结构呈现出连续的韧脆和脆韧转变区域，因此每次脆韧脆转变都伴随着冲击时间内的显著载荷下降。再熔融过程被证实可使未辐照试样的断口表面韧性更高，且条纹数量更少。而辐照产生的断口表面无条纹，这与较低的冲击韧性一致。除了证实辐射剂量和再熔融处理对冲击行为的主导作用外，这些作者还提出分子链长度可能是解释冲击行为差异的一个相关特性，具有相似分子量但线性特征（即支化含量）不同的未辐照树脂（GUR 1050和MG003）。根据其制造商（DSM医疗生物材料公司，荷兰）的说法，MG003树脂相比GUR 1050具有更线性、支化程度更低的主链结构，这可能是导致先前研究中发现其冲击韧性最低的原因[93]。实际上，研究人员可能会希望通过调节超高分子量聚乙烯树脂的分子量和支化特性来进一步优化其断裂性能，正如在其他领域所进行的那样。

36.3.4 弹塑性断裂力学与J积分概念

如第36.2.4节所述，应力强度因子K描述了裂纹尖端附近的应力状态。然而，K并不完全是断裂的“驱动力”。能量释放率G定义为裂纹面积增量A对应的势能变化∏：

$$ G = -\frac{d\Pi}{dA} $$

其中G是裂纹扩展的“驱动力”，因为它是与裂纹扩展相关的势能梯度，其单位为能量/面积。当该能量释放率超过临界值时，裂纹扩展所导致的能量释放速度超过了材料对裂纹扩展的抵抗能力，系统变得不稳定，发生快速断裂。因此，G描述了亚临界行为和快速断裂的条件。在线弹性各向同性材料中，G与K之间存在直接对应关系。

$$ G = \frac{K^2}{E’} $$

其中E’为弹性模量E，在平面应力状态下，或在平面应变状态下为E/(1−v²)。耗散能的概念非常重要，因为它能够在不丢失裂纹扩展过程中裂纹尖端条件任何信息的情况下，抽象出这些条件的细节。采用能量概念（例如裂纹扩展所导致的耗散能）是克服线弹性断裂力学在存在非线性、塑性和时间相关效应时局限性的有效方法。

当线弹性断裂力学（LEFM）不准确时，分析断裂的一种有效方法涉及J积分路径积分，也称为J积分或简称为J。它是围绕裂纹尖端的闭合围线积分的路径无关值，表示在单调加载循环期间用于扩展裂纹所消耗的总能量[95]：

$$ J = \int_\Gamma \left( w dy - T \cdot \frac{\partial u}{\partial s} dx \right) $$

其中Γ是路径或轮廓，w是材料的应变能密度，y和x是坐标方向，T是面力矢量，u是位移矢量，s是沿轮廓的弧长。

这项及相关工作的基本结论是，尽管裂纹附近的材料行为可能是非弹性的，但弹塑性材料的单调应力‐应变曲线与非线性弹性材料的单调应力‐应变曲线并无区别。这一事实使得通过远程计算与裂纹扩展相关的总能量（忽略循环效应）来分析弹塑性断裂成为可能，其中包括发生在远离裂纹尖端区域的变形过程。

J积分以与G对线弹性材料相同的方式计算非线性弹性材料在裂纹扩展时的势能变化。因此，对于线弹性材料，G = J。此外，J已被用于描述幂律硬化弹塑性材料中裂纹尖端的应力强度。这类材料常用的单轴应力–应变关系为拉姆伯格‐奥斯古德关系，其表达式为

$$ \varepsilon = \varepsilon_y + \alpha \left( \frac{\sigma}{\sigma_y} \right)^n $$

其中ε和εy分别为应变和屈服应变，而σ和σy分别为应力和屈服应力，n和a为材料拟合参数。幂律硬化材料中裂纹尖端附近的应力由所谓的HRR方程[96]描述，该方程以提出它的作者哈钦森、赖斯和罗森格伦的名字命名：

$$ \sigma_{ij} = \frac{k_1}{(J/r)^{1/(n+1)}} f_{ij}(n, \theta) $$

在HRR方程中，k₁是一个比例因子，它是材料属性（即a、E和σy）、几何形状、θ、r（裂纹尖端距离）以及塑性幂律硬化指数n的函数。

根据拉姆伯格‐奥斯古德关系。注意，奇异性强度取决于n，而该场的相对强度由刚度和屈服强度决定。如果n为1，则公式36.16在数学上退化为线弹性断裂力学的一个类似形式，因为此时拉姆伯格‐奥斯古德关系变为线性方程。

另一个有用的关系将J值与裂纹尖端张开位移（CTOD）δ联系起来，该位移定义了裂纹面在裂纹尖端附近被拉开的距离，是材料韧性和延展性的度量。这一关系如公式36.17所示，在线弹性断裂力学（LEFM）的适用范围之外仍然成立[31]，其中σf为材料在裂纹尖端处的流动应力。

$$ J = \sigma_f \delta $$

这种关系有助于量化非线性弹性材料中耗散的能量，从而确定驱动力，特别是在δ容易观察或作为方便的物理参数进行跟踪的情况下。

36.3.5 基于J积分的断裂韧性测试

36.3.5.1 多试样与单试样方法

通常建议采用单边缺口三点弯曲、紧凑型和盘状紧凑型试样进行基于J积分的断裂韧性评估。测试前，超高分子量聚乙烯试样通常在疲劳条件下或其他切口技术作用下进行预开裂，以在机加工缺口根部诱导出尽可能尖锐的预先存在的裂纹。预开裂后，将试样（或多试样法中的一系列试样）以恒定速率加载至选定的位移水平，以引发稳定的裂纹扩展或撕裂。根据ASTM E1820[97]（最初为金属开发的标准），可采用两种不同的方法，具体取决于裂纹扩展的测量方式。基本的（多试样）法依赖光学方法测量裂纹长度，而弹性柔度技术则用于阻力曲线（单试样）法中提供裂纹长度估算。尽管无法通过多试样法构建有效的J积分与裂纹扩展关系的J–R曲线，但仍可计算所有试样的J值和裂纹长度。

需要进行测试以获得萌生韧性JIC值。J根据以下方程，通过弹性分量Je和塑性分量Jpl的总和计算得出：

$$ J = J_e + J_{pl} = \frac{K^2 (1 - \nu^2)}{E} + \frac{\eta_p A_{pl}}{B b_o} $$

$$ K = \frac{P}{B_N \sqrt{W}} f \left( \frac{a_o}{W} \right) $$

其中，K为应力强度因子，f(a₀/W)是原始裂纹长度a₀和试样宽度W的函数，ν为泊松比，E为杨氏模量E，b₀为原始未裂韧带b₀，即W减去a₀，BN为净厚度（若试样无侧槽，则为B），η为考虑未裂韧带与试样宽度之比的几何系数（η = 2 + 0.522b₀/W），最后，Apl为载荷‐位移曲线中对应于试样塑性变形部分下方的面积。当达到选定的位移后，将试样卸载，并可对裂纹进行标记，以利于后续长度测定。然后需要使试样完全断裂，以暴露裂纹，通过光学或扫描电镜（SEM）在九个点测量原始裂纹尺寸a₀和最终实际裂纹尺寸ap，其中两点靠近表面（距边缘0.005W处），其余七点在断口表面上均匀分布。两个近表面测量值的平均值与其余七个裂纹长度测量值结合，用于计算裂纹长度的最终平均值。绘制J值随裂纹扩展量的变化曲线∆a = ap − a₀后，可得到初始稳定裂纹扩展时的J值JIC。JIC的估算需要根据以下方程确定并绘制一条构造线（或钝化线）：

$$ J = M \sigma_f \Delta a $$

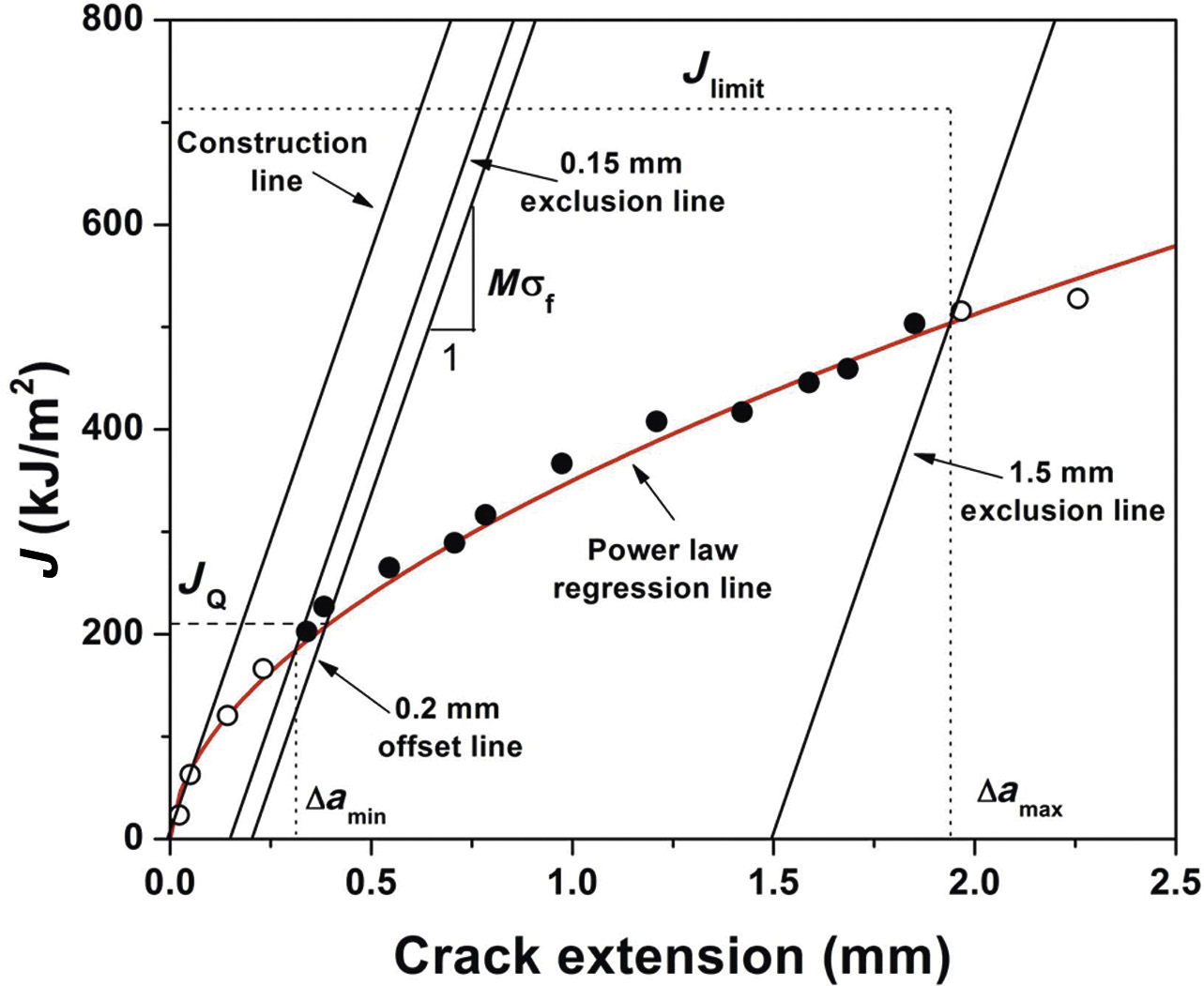
其中，M = 2或通过线性回归法确定为0.2JQ ≤ Ji ≤ 0.6JQ区域内至少六个数据点的回归线斜率。如前所述，σf是裂纹尖端前方弹塑性材料中的流动应力。然后，绘制两条与构造线斜率相同的排除线，使其分别在横坐标轴上0.15和1.5毫米处与x轴相交。此外，还需绘制一条与构造线和排除线平行的偏移线，使其与横坐标相交。

在0.2 mm处（图36.14）。最后，根据以下幂律表达式确定数据的回归线：

$$ \ln J = \ln C_1 + C_2 \ln \Delta a $$

该回归线与偏移线的交点（见图36.14）定义了J、JQ以及裂纹扩展量∆aQ的中间值。JQ是JIC的合适度量，只要系数C₂小于1，且试样的厚度和初始无裂纹ligament大于25JQ/σf，并且幂律回归线在∆aQ处的斜率小于σf。

需要指出的是，对于超高分子量聚乙烯（UHMWPE），流动应力σf的取值存在一定争议。根据ASTM E1820标准，传统上将其定义为所谓的有效屈服强度，即0.2%偏移屈服强度σy与抗拉强度UTS的平均值。然而，对于UHMWPE，流动应力也曾被定义为屈服强度σy或抗拉强度UTS[11,98–100]。流动应力的选择显然会影响J值的计算结果，这一模糊性在该领域中仍然是一个难题。近期的研究已着手解决流动应力[11]的不确定性问题，具体将在以下章节中详述。

由于柔度测量不需要试样的完全断裂即可评估裂纹扩展，在阻力曲线法中，通过对单个试样进行连续的卸载‐加载循环，以促进每一步产生更长的裂纹扩展。构建J–R曲线依赖于在每一步i处，基于载荷线（即柔度测量）上测得的裂纹张开位移，计算Ji和裂纹长度ai以及载荷Pi。对于带侧槽的紧凑拉伸试样，所用方程如下：

$$ J_i = \frac{K_i^2 (1 - \nu^2)}{E} + J_{pl(i)} $$

$$ U_x = \frac{1}{E B_V} \left[ 1 + \frac{P_i}{V} \right] $$

$$ a_i = W \left[ C_0 + C_1 U_x + C_2 U_x^2 + C_3 U_x^3 + C_4 U_x^4 + C_5 U_x^5 \right] $$

其中Ki为载荷Pi下的应力强度因子，ν为泊松比，E为弹性模量，Jpl(i)表示考虑试样塑性变形的修正项，Ux为归一化柔度，V为测量点之间的位移，V/Pi为柔度，Be = B – (B – BN)²/B，其中B为试样厚度，BN为净厚度，W为试样宽度。在通常情况下，柔度法假设对于给定的试样几何形状，归一化柔度Ux与归一化裂纹长度a/W之间的关系是唯一的[10]。这意味着任何线弹性、各向同性且均匀的材料都应遵循相同的U与a/W曲线，从而定义公式36.24中的标准柔量系数。然而，这些标准系数不适用于传统超高分子量聚乙烯或高度交联的超高分子量聚乙烯配方，正如瓦拉达尔詹和里姆纳克[10]所示，必须对每种不同的配方通过实验确定相应的系数。最后，试样的厚度B，以及原始b₀和最终b的未裂韧带，决定了J积分的最大承载能力及最大裂纹扩展量，分别取Jmax = bσf/20或Jmax = Bσf/20中的较小值，以及∆amax = 0.25b₀。此外，也可按照类似于多试样法的步骤计算韧性的萌生值。

36.3.5.2 J积分和单试样归一化法

ASTM E1820中描述的多试样和单试样方法均存在明显缺点。基本的多试样法耗材且耗时，且无法获得严格有效的J–R阻力曲线。另一方面，单试样法或阻力曲线法依赖弹性柔度法来评估裂纹扩展。虽然柔度法适用于金属，但对于表现出时间相关性能（即粘弹性行为）的材料，如聚合物，这类材料的裂纹扩展测量会变得复杂且不准确。归一化法可用于测量裂纹扩展，克服其中一些局限性，同时仍使用单个试样。该方法的描述见参考文献瓦拉达尔詹和里姆纳克、Landes等人以及ASTM E1820[11,101,102]。

归一化法基于以下假设：载荷可以表示为裂纹长度和位移的可分离函数的乘积。因此，如果已知载荷和位移，则可以通过此关系计算裂纹长度：

$$ P = G \left( \frac{a}{W} \right) H \left( \frac{\nu_{pl}}{W} \right) $$

其中a和W分别为裂纹长度和试样宽度，νpl是位移的塑性分量。G仅是裂纹长度与宽度归一化后的函数，而H仅是归一化塑性位移的函数。因此，对于一个静止的裂纹，载荷可能由于裂纹长度和塑性位移的变化而发生变化。G和H函数由以下关系给出：

$$ G \left( \frac{a}{W} \right) = \frac{\eta_{pl} W B}{b} $$

$$ H \left( \frac{\nu_{pl}}{W} \right) = L + M \left( \frac{\nu_{pl}}{W} \right) + N \left( \frac{\nu_{pl}}{W} \right) $$

其中，B为试样厚度，b为未裂韧带，W – a，ηpl来源于J的标定，而L、M和N为未知的拟合常数。需要注意的是，在试验过程中记录的是总位移ν，而非塑性位移νpl。总位移由弹性项和塑性项组成：

$$ \nu = \nu_{el} + \nu_{pl} $$

$$ P = C \left( \frac{a}{W} \right) \nu_{el} $$

其中C(a/W)为柔度函数，其取决于裂纹长度和载荷。由于P是裂纹长度和塑性位移的函数，而后者又通过柔度函数依赖于裂纹长度，因此方程36.25–36.29需以迭代方式求解。另一方面，H函数反映了材料的应力‐应变行为（实际上，有时称H为硬化函数），因此L、M和N常数并非先验假设，因为不同试样之间可能存在差异。这些常数在试验过程中通过对每个试样选取三个标定点来确定，通常选在试验开始和结束时，以及接近最大载荷处。对于初始和最终标定点，需要在暴露的断口表面上测量实际裂纹长度；而对于第三个标定点，则假设并调整校准值以优化拟合函数。然而，测量初始裂纹长度点可能存在困难，因此可在特定的位移范围内选取一组标定点，即所谓的可分离钝化区，在该区域内表观裂纹扩展被认为完全由钝化引起（详见Varadarajan和Rimnac[11]的详细说明）。在确定L、M和N之后，便可求解方程36.25–36.27以得到裂纹根据测试中的载荷和位移给出长度结果。最后，J值可通过应用公式36.18和36.22获得。

瓦拉达尔詹和里姆纳克验证了用于超高分子量聚乙烯J积分断裂韧性测试的单试样归一化法[11]。此外，他们还解决了流动应力的争议问题，因为在裂纹尖端应采用何种适当的流动应力来计算J值方面，无论是通过钝化线还是基于裂纹尖端张开位移的技术，目前尚未达成一致意见。如前所述，屈服强度、抗拉强度以及有效屈服强度均曾被用作流动应力，以获得基于J积分的超高分子量聚乙烯材料断裂韧性测量结果[11,98–100,102]。需要注意的是，将抗拉强度或屈服应力作为流动应力会对J积分的计算值产生关键影响（如前所述），因为传统和高交联超高分子量聚乙烯配方具有相似的屈服强度，但极限强度却显著不同[6]。瓦拉达尔詹和里姆纳克的工作概述了指定流动应力的各种方法。他们还通过一种新型裂纹尖端张开位移方法进行了实验，证明将抗拉强度作为流动应力是合适的。尽管如此，瓦拉达尔詹和里姆纳克建议避免使用钝化线方法，因为流动应力本身存在固有的模糊性。相反，他们建议在裂纹尖端张开位移δ,于载荷施加后其增长突然减小的条件下确定JIC值。他们对表观裂纹扩展的不连续增加以及δ增长减缓现象的研究，并且该现象与Jc的变化相一致，在概念上也吻合在循环加载中，关于裂纹尖端耗散功的类似观察，称为滞后法（见下文）。

36.3.5.3 为聚合物开发的基于J积分的方法

迄今为止，所描述的方法最初是为金属材料的测试而开发的，尽管它们已被应用于研究聚合物和其他材料。目前，仅存在一种专门为聚合物开发的基于J积分的标准协议，可在ASTM D6068[103]中找到。其他非常规协议，例如卢等人针对增韧丙烯腈‐丁二烯‐苯乙烯开发的滞后环法，在聚合物文献中也有记载[85,104,105]，但这些方法基于聚合物的粘弹性特性。

ASTM D6068描述了一种多试样程序，类似于ASTM E1820中所述的方法。建议使用带预切口或疲劳预制裂纹的三点弯曲和紧凑型试样进行测试。同样，将试样加载至选定的位移，该位移被认为可引起一定的裂纹扩展，然后将其断裂以暴露断口表面。除了记录载荷‐位移曲线外，还需对每个试样的初始和最终裂纹长度进行光学评估，以获得五点平均裂纹长度。例如，用于裂纹长度评估的未辐照样品以及100 kGy电子束辐照并重熔的超高分子量聚乙烯的典型SEM显微照片如图36.15A和B所示。最终构成J–R曲线的数据点必须满足某些资格要求，以便

要被视为有效数据点，需满足与ASTM E1820中规定类似的要求。具体而言，构建一条J–R曲线至少需要七个数据点，这些数据点还必须均匀分布在由0.05毫米排除线和∆amax = 0.1bo排除线所定义的区域内，且第一象限（小裂纹扩展）内至少应有三个数据点。J需对压痕能Ui进行修正，并通过以下关系式计算得出：

$$ J = \frac{\eta U_T}{B (W - a_o)} $$

$$ U_T = U_i + U $$

其中，B、W、a₀分别为试样的厚度、宽度和原始裂纹长度，η对于紧凑试样等于2 + 0.522b₀/W，UT和U分别为总能量和裂纹扩展所需能量。最后，对数据进行幂律回归拟合，并确定J–R曲线。通过该方法得到的J–R曲线可用于对不同聚合物或经不同处理或加工条件下的聚合物进行排序。

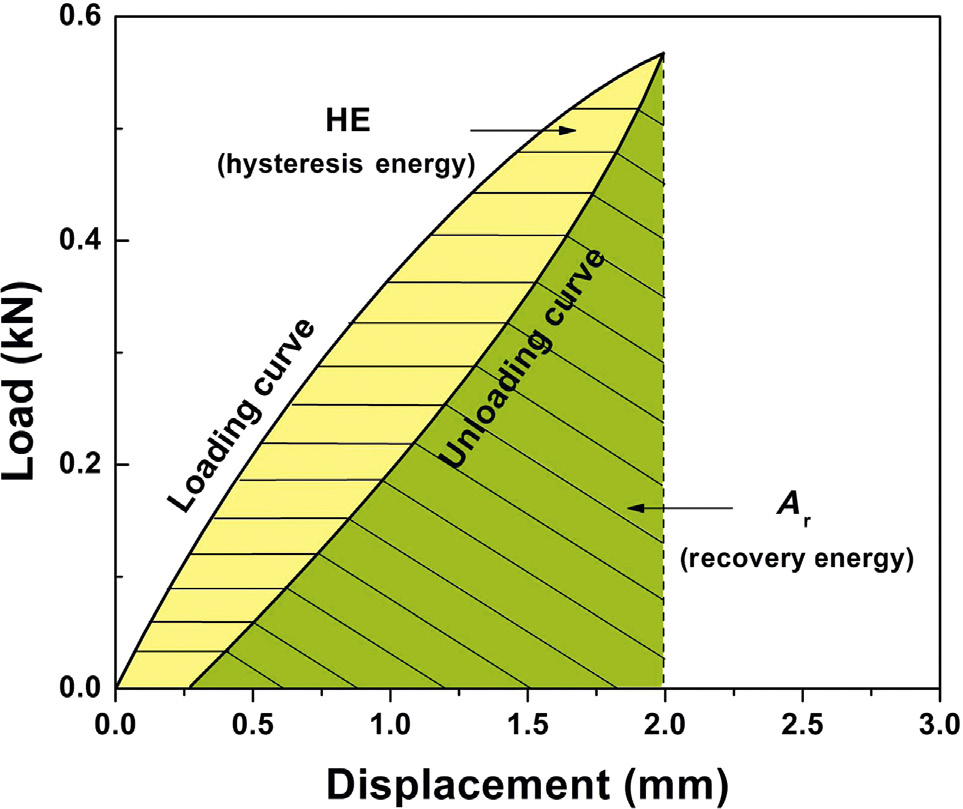
滞后环法基于某些预制裂纹聚合物试样在循环加载和卸载过程中载荷‐位移曲线的行为（参见图36.16）[104,105]。输入能量（即载荷‐位移曲线加载段曲线下面积Ao）与恢复能量（即卸载段曲线下面积Ar）之间存在明显差异。滞后能可定义为输入能量与恢复能量之差。从物理角度而言，滞后能主要被认为是用于扩大裂纹扩展起始前裂纹尖端塑性区所消耗的能量。然而，一旦裂纹扩展开始，应变能释放也将对滞后能产生贡献，从而在裂纹钝化与裂纹扩展之间形成该性能的转变，并由此估算出JIC值。滞后能HE可通过定义滞后比HR来计算，其表达式由以下方程给出：

$$ HR = \frac{A_o - A_r}{A_o} $$

然后HE由下式给出：

$$ HE = HR \cdot U $$

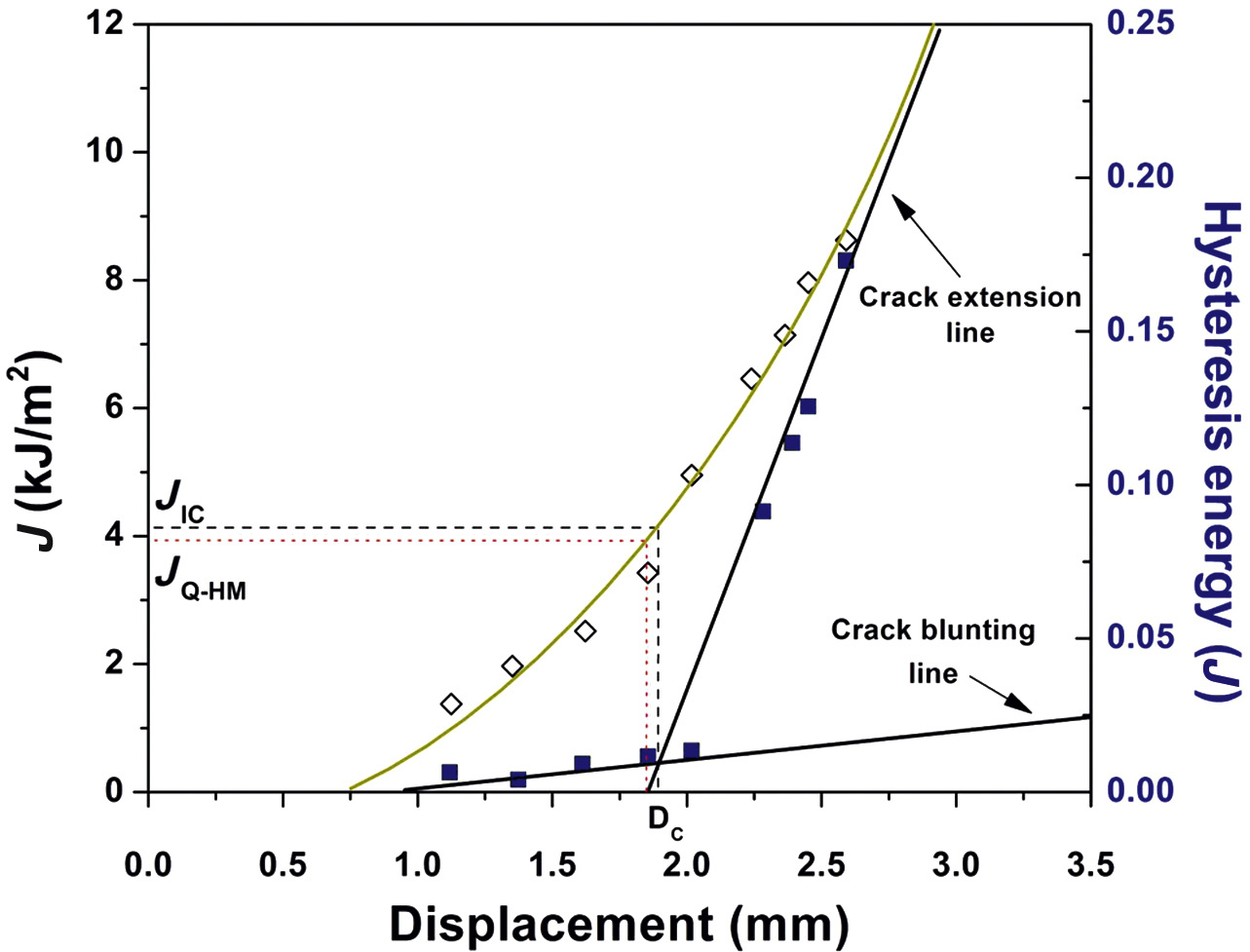
其中U是在选定的位移下加载曲线下的能量。通过将常用的J和HE结果一起表示，可以确定一个JIC估计值，即对应于临界位移Dc的J值，该临界位移是裂纹钝化线与裂纹扩展线相交处的位移（见图36.17）。裂纹扩展起始前后滞后能量数据的线性回归定义了裂纹钝化线与裂纹扩展线之间的转变。显然，滞后环法的主要优点是无需测量裂纹长度，从而避免了关于裂纹钝化和流动应力的争议。然而需要注意的是，Lu的研究中采用了恒定裂纹速度条件，因此他们认为使用完整加载‐卸载循环的滞后比是合适的。通常情况下，滞后比将是局部应变、应变率、温度以及裂纹增长量的函数[105]。

刘易斯和尼曼采用迟滞法的一种变体，研究了经不同灭菌方法处理并进行加速老化后超高分子量聚乙烯（UHMWPE）的断裂抗力[85]。在本研究中，单个试样在三点弯曲配置下加载，记录载荷P与位移D的关系曲线，直到位移达到8 mm。计算了P–D曲线下至六个选定的位移Di处的面积，并用于获得相应的Ji值。将Ji-Di数据对进行绘图，并对数据点进行了最佳拟合曲线。绘制了渐近裂纹扩展线，其与位移轴的交点定义为临界位移Dc（见图36.17）。材料的暂定断裂韧性JQ-HM由对应于J值给出，该值对应于Dc。最后，必须满足以下方程才能将JQ-HM视为有效的JIC值：

$$ B, b_o > \frac{25 J_{Q-HM}}{\sigma_f} $$

其中B为试样厚度，bo为原始未开裂韧带，流动应力σf定义为0.5(σy +抗拉强度)，即有效屈服强度。

刘易斯和尼曼采用该方法获得的超高分子量聚乙烯断裂性能的主要研究结果总结于第36.3.6节。

36.3.6 超高分子量聚乙烯的J积分断裂韧性

关于超高分子量聚乙烯断裂韧性表征的科学报告反映了前文所述J积分方法的多种变体。多种试样方法，例如为金属所描述的方法，ASTM E1820以及现已废止的ASTM E813，或专为塑料开发的ASTM D6068，已被修改并应用于超高分子量聚乙烯[8,98–100,106,107]。另一方面，其他单试样方法，即归一化法和滞后环法，也提供了对超高分子量聚乙烯稳定裂纹扩展抗力的估算[11,85,101]。在接下来的段落中，将概述关于超高分子量聚乙烯断裂韧性的主要研究结果。

里姆纳克等人基于ASTM E813 87[100,108]-中描述的多试样方法，估算出柱塞挤出的超高分子量聚乙烯的JIC值为99.5 kJ/m²。在本研究中，通过将流动应力指定为抗拉强度以获得钝化线，并采用常规的0.15和1.5毫米排除线对数据进行了评定。帕斯科等人采用了相同的多试样方法来测定柱塞挤出的GUR 4150超高分子量聚乙烯的JIC，但他们考虑了五种不同的分析方法，从J与裂纹扩展关系曲线中计算JIC，试图找出最佳方法[99]。该研究中所包含的各种方法得出的JIC值范围从27 kJ/m²到238 kJ/m²不等。然而，作者提出了一种改进的分析方法，即在J–R数据之间进行线性拟合∆a/bo = 0.6%，并且w = (bo/J)(dJ/d∆a) > 3。JIC是通过R曲线与钝化线的交点获得的，其中流动应力采用抗拉强度UTS计算得到。根据这种改进的滞后环法，沿挤出方向加工的GUR 4150超高分子量聚乙烯试样表现出的JIC值为66.5 kJ/m²。在进一步的研究中，相同作者发现，在空气中进行伽马辐照灭菌（25–40 kGy）会使超高分子量聚乙烯的韧性降低50%[109]。刘易斯和尼曼[85]还报告指出，基于改进的滞后环法，伽马辐照灭菌后超高分子量聚乙烯的断裂韧性从92 kJ/m²降至44.3 kJ/m²。此外，在高温（70摄氏度）和氧压（507千帕）条件下进行2周的加速老化，会导致经伽马辐照灭菌的超高分子量聚乙烯断裂韧性严重下降，韧性降低至1.9 kJ/m²。尽管受影响程度小于经伽马辐照灭菌的超高分子量聚乙烯，但未灭菌、环氧乙烷灭菌以及气体等离子灭菌的超高分子量聚乙烯对人工老化也并非完全免疫。

关于高交联度超高分子量聚乙烯，吉利斯等人在连续进行的两项研究中利用ASTM E813‐81标准评估了高交联超高分子量聚乙烯的断裂抗力