【动手学深度学习 | week1b】05 线性代数 06矩阵计算 07 自动求导

05 线性代数

标量

# 实例化标量
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)

向量

向量可以看作由标量组成的列表，在数据表示中，一个向量的各个元素可以表示各个指标数据

# 定义一个向量
x = torch.arange(4)
# 通过张量的索引来访问任一元素
x[3] ## index从0开始

维度:向量的长度，也就是数组的长度

len(x) 

• 简单操作：相加，相乘
• 长度：各个元素平方求和开根号

矩阵

概念：

• 简单操作：相加，相乘
• 矩阵之间的乘法：
  矩阵乘向量。可以理解为矩阵把向量的空间进行了扭曲。
  矩阵乘矩阵。mn*nc
• 范数：矩阵的长度。hence $||A||$。常见的有矩阵范数和F范数，两种计算方式不一样。
• 对称矩阵、饭对称矩阵，正定矩阵，正交矩阵，置换矩阵
• 特征向量：不被矩阵改变方向的向量，对称矩阵总是可以找到特征向量。

# 每个矩阵可以看作是一个表格，可以使用两个分量m,n来创建一个m*n的矩阵
A = torch.arange(20).reshape(5, 4)
# 矩阵的转置，对称矩阵的转置等于自己
A.T

张量

就像向量是标量的推广，矩阵是向量的推广一样，我们可以构建具有更多轴的数据结构。张量（本小节中的“张量”指代数对象）为我们提供了描述具有任意数量轴的 𝑛 维数组的通用方法。例如，向量是一阶张量，矩阵是二阶张量。

# 创建一个3阶张量，实际以n维数组的形式存在，例如三维表示高度、宽度和多个channel
X = torch.arange(24).reshape(2, 3, 4)

张量算法的基本性质：给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

哈德码积 Hadamard积：两个矩阵的按元素乘法

A * B
# 将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

降维

计算其元素的和：调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量

x = torch.arange(4, dtype=torch.float32)
x, x.sum()
# 表示任意形状张量的元素和，一个5*4的矩阵元素求和
A.shape, A.sum()
# 指定张量沿哪一个轴来通过求和降低维度，调用函数时指定axis=0，输入轴0的维数在输出形状中消失
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
# 沿着行和列对矩阵求和，等价于对矩阵的所有元素进行求和。
A.sum(axis=[0, 1])  # SameasA.sum()
# 求均值。也就是先求和，再除数量。
A.mean(), A.sum() / A.numel()
# 按维度求和
A.mean(axis=0), A.sum(axis=0) / A.shape[0]

非降维求和（广播机制使用）

不要丢掉维度。调用函数来[计算总和或均值时保持轴数不变]会很有用

sum_A = A.sum(axis=1, keepdims=True)
sum_A
# 由于sum_A在对每行进行求和后仍保持两个轴，我们可以(通过广播将A除以sum_A)，因为广播机制要求数据的维度必须是一样的，如果被降维了就没法进行运算
A / sum_A
# 某个轴计算A元素的累积总和，这个操作不会降低维度
A.cumsum(axis=0)

点积（Dot Product）

点积：相同位置的按元素乘积的和 $<x,y>$

y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)
# 我们可以通过执行按元素乘法，然后进行求和来表示两个向量的点积，这也解释了点积的作用
torch.sum(x * y)

矩阵-向量积（matrix-vector product）

矩阵向量积 𝐀𝐱 是一个长度为 𝑚 的列向量， 其第 𝑖 个元素是点积 ${\mathbf{a}}_i^{\top }\mathbf{x}$

们可以把一个矩阵 $\mathbf{A}\in R^{m\times n}$ 乘法看作是一个从 $R^n$ 到 $R^m$向量的转换。这种向量转换是非常有用的

#在代码中使用张量表示矩阵-向量积，我们使用与点积相同的mv函数
#当我们为矩阵A和向量x调用torch.mv(A, x)时，会执行矩阵-向量积。 注意，A的列维数（沿轴1的长度）必须与x的维数（其长度）相同。
A.shape, x.shape, torch.mv(A, x)

矩阵-矩阵乘法

我们可以将矩阵-矩阵乘法 𝐀𝐁 看作是简单地执行 𝑚 次矩阵-向量积，并将结果拼接在一起，形成一个 𝑛×𝑚 矩阵。

# 矩阵-矩阵乘法可以简单地称为矩阵乘法，不应与"Hadamard积"混淆。
# 函数是mm
B = torch.ones(4, 3)
torch.mm(A, B)

范数（norm）

一个向量的范数告诉我们一个向量有多大，里考虑的大小（size）概念不涉及维度，而是分量的大小。
在线性代数中，向量范数是将向量映射到标量的函数 𝑓 。
定任意向量 𝐱 ，向量范数要满足一些属性。 第一个性质是：如果我们按常数因子 𝛼 缩放向量的所有元素， 其范数也会按相同常数因子的绝对值缩放：𝑓(𝛼𝐱)=|𝛼|𝑓(𝐱).
第二个性质(三角不等式)：𝑓(𝐱+𝐲)≤𝑓(𝐱)+𝑓(𝐲).
第三个性质（非负性）：𝑓(𝐱)≥0.
如果一个范数是0，那么应该是所有向量都由0组成，这样所有分量都是0.

范数听起来很像距离的度量。 如果你还记得欧几里得距离和毕达哥拉斯定理，那么非负性的概念和三角不等式可能会给你一些启发。 事实上，欧几里得距离是一个 𝐿2 范数： 假设 𝑛 维向量 𝐱 中的元素是 𝑥1,…,𝑥𝑛 ，其[ 𝐿2 范数是向量元素平方和的平方根：]
$$\Vert \mathbf{x}{\Vert }_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$
其中，在 𝐿2 范数中常常省略下标 2 ，也就是说 ‖𝐱‖ 等同于 $\Vert \mathbf{x}{\Vert }_2$

# 范数是norm
u = torch.tensor([3.0, -4.0])
torch.norm(u)

[ 𝐿1 范数，它表示为向量元素的绝对值之和：]

# 将绝对值函数和按元素求和组合起来。
torch.abs(u).sum()

类似于向量的 𝐿2 范数，矩阵$\mathbf{X}\in R^{m\times n}$ (的Frobenius范数（Frobenius norm）是矩阵元素平方和的平方根(概念从向量转变到了矩阵)

torch.norm(torch.ones((4, 9)))

在深度学习中，我们经常试图解决优化问题： 最大化分配给观测数据的概率; 最小化预测和真实观测之间的距离。 用向量表示物品（如单词、产品或新闻文章），以便最小化相似项目之间的距离，最大化不同项目之间的距离。 目标，或许是深度学习算法最重要的组成部分（除了数据），通常被表达为范数。

06 矩阵计算

主要目的就是知道矩阵怎么求导数。
导数的作用是主要是进行梯度的计算
需要知道Input不同的形状下，得出的导数的形状是什么样子的

标量导数

亚导数

亚导数就是在不可微的点上，导数是一个范围中的值

向量的导数

梯度：指向值变化最大的方向

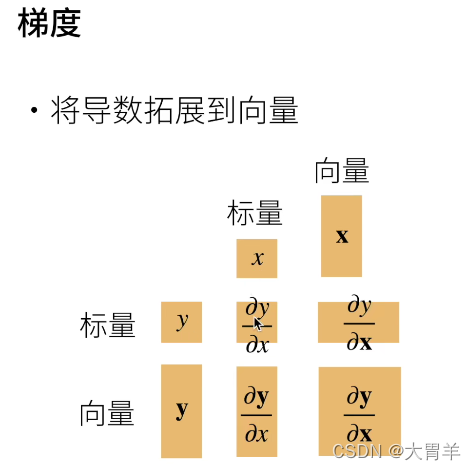
标量关于向量

可以用等高线理解：梯度和等高线正交，梯度指向值变化最大的方向。
$y$是标量，$X$是向量

求导的例子：

向量关于标量

向量关于向量：列向量，每一行又是一个维度的处理，所以处理后会是一个矩阵。

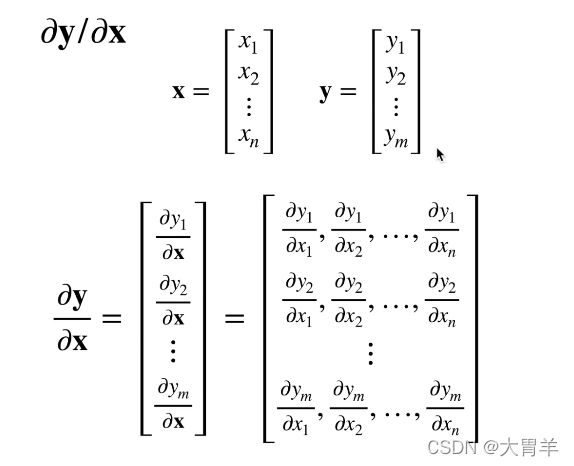
扩展到矩阵

**向量与标量：**矩阵在下面，结果会转置一下。矩阵在上面，但是不会变。
2维与2维求导得三维，三维与三维求导得四维。
各个维度的变化规律可以参考下图：

07 自动求导

向量链式法则

其实就是微分求导的过程。

线性回归的例子：注意求导变转置的过程：

自动求导

计算一个函数在指定值上的导数，和符号求导以及数值求导（拟合求导），根本是计算图的概念。
将代码分解为操作子，也就是链式法则的求导过程，表示为一个无环图。

自动求导的两种模式：

因为现在链式求导给了我们$u_1$到$u_n$的操作子，所以区别就是，我们从$u_n$开始计算（反向累积），还是从$u_1$开始计算（正向累积）

• 正向积累
  

• 反向累计、反向传递
  
  计算概念对比：
  正向需要存储所有的中间计算结果，不然无法得到下一步的结果。
  反向需要正向计算时部分的操作子结果，但是不用把所有反向的操作子存储下来，可以去除不必要的枝节。
  
  
  复杂度对比：正向和反向的代价是类似的。但是正向需要存储所有中间结果，所以非常消耗中间结果。

实际操作

深度学习框架通过自动计算导数，即自动微分（automatic differentiation）来加快求导。 实际中，根据我们设计的模型，系统会构建一个计算图（computational graph）， 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

假设我们想对函数 𝑦=2𝐱⊤𝐱 关于列向量 𝐱 求导：

import torch
# 创建一个长为4的向量
x = torch.arange(4.0)
# 需要一个地方来存储梯度
x.requires_grad_(True)  # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad  # 默认值是None
# 计算y
y = 2 * torch.dot(x, x)
# 调用反向传播函数来计算y对于x每个分量的梯度
y.backward()
x.grad
# 验证一下梯度
x.grad == 4 * x
# 计算x的另一个函数，注意需要先清除梯度，因为梯度一般都是累积的
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
#如果y不是标量，非标量变量的反向传播：

非标量变量的反向传播（向量和矩阵）

当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。 对于高阶和高维的y和x，求导的结果可以是一个高阶张量。

然而，虽然这些更奇特的对象确实出现在高级机器学习中（包括[深度学习中]）， 但当我们调用向量的反向计算时，我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。 这里(我们的目的不是计算微分矩阵，而是单独计算批量中每个样本的偏导数之和)。不直接计算向量，而是分开计算，然后求和。

# 对非标量调用backward需要传入一个gradient参数，该参数指定微分函数关于self的梯度。
# 在我们的例子中，我们只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward() #先求和，再反向传播求梯度
x.grad

分离计算

将某些计算移动到记录的计算图之外，用于把参数固定住，而不是还有变量在其中

x.grad.zero_()
y = x * x
u = y.detach() #u和x没有关系，就是一个常数了
z = u * x

z.sum().backward() #这个时候求梯度，u只是作为一个标量，不会产生额外的影响。
x.grad == u

Python控制流的梯度计算

自动微分的好处：即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度。因为这个过程不会改变输入a。

# 定义一个循环函数
def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
# 计算梯度值
a = torch.randn(size=(), requires_grad=True) # 对于控制流的语句，由于会存储所有的值，所以并不影响梯度计算。注意:输入a中是分段线性的
d = f(a)
d.backward()
# 梯度验证（）
a.grad == d / a #对于任何a，存在某个常量标量k，使得f(a)=k*a，所以梯度就是k