上一篇文章讲了SwiGLU(Switch-Gated Linear Unit)门控线性单元激活函数:
混合专家模型前传-------SwiGLU(Switch-Gated Linear Unit)门控线性单元激活函数-优快云博客
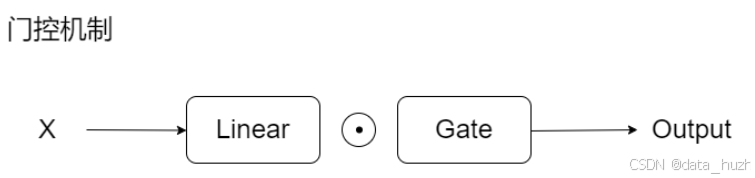
门控机制就是控制 进过线性层后的X 输出的一个门,
我们把其中一个线性层看作携带信息的层,把另一个线性层看作“门控机制”,以此来压缩数据的通路、逼迫模型筛选出更精准、更重要的信息。
从门控机制出发我们可以设想,如果我们不止一扇门呢?这是否意味着我们可以拥有动态的筛选策略?是否意味着我们可以同时筛选出不同、但都非常重要和精准的信息?就如同卷积神经网络利用不同的卷积核解读不同的信息、注意力机制用不同的头来解读不同的信息一样,门控机制中我们也可以有不同的门来用不同的方式筛选信息,混合专家模型因此而诞生,让我们来看看混合专家模型——
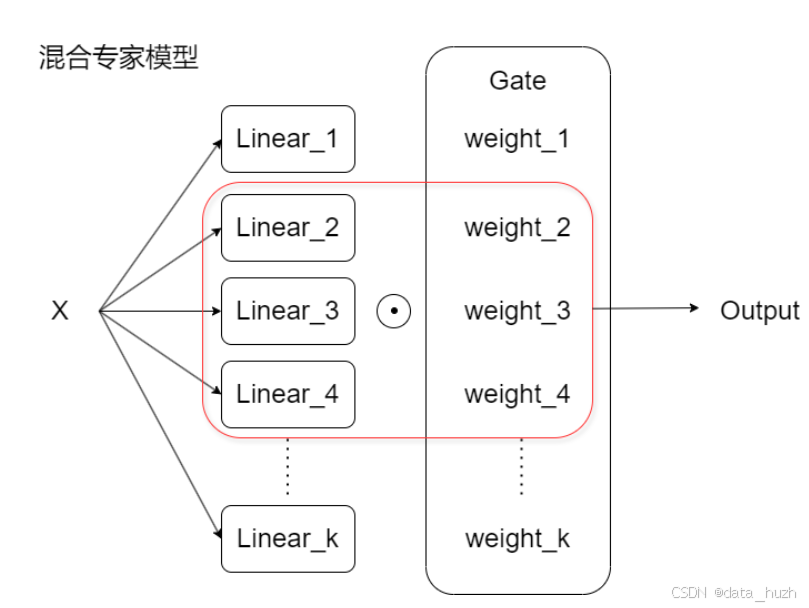
当我们使用多个门同时控制信息的流通时,这些多个门构成的结构被称为是路由器。
混合专家模型 (MoE) 是一种动态路由策略,通过为不同的输入选择不同的子模型(专家模型)进行计算。MoE每次向前传播时,只激活部分专家模型,从而实现参数高效和计算高效。
所以同等规模下,MoE推理速度更快。因为计算参数时各个专家都被计算在内,但每次训练或推理时,只用部分参数来计算。所以模型可以在有超大参数量时,同时保持很快的推理速度。
MoE与Transformer架构或LLaMA架构有什么关系?
MoE作为很好的输出模型,可以用于代替Transformer中的前馈网络(FFN)层。
- 提高模型表达能力
在传统FFN中,每一层用相同参数处理所有输入。限制了模型表达能力
在 MoE 中,不同的专家网络可以学习不同的模式,每次处理输入时,动态选择不同的专家来增强模型的灵活性。 - 参数量高但计算量低
- 增强泛化能力
每个专家专注于学习特定模式,有助于减小模型过拟合,提高泛化能力
MoE损失函数
在 Mixture of Experts (MoE) 模型中,常见的辅助损失(auxiliary loss)用于帮助训练过程中的专家选择更加平衡,防止某些专家被过度选择或其他专家很少被选中。
N是专家数量
Pi是所有专家平均权重
fi是专家平均使用率
最后的辅助损失是所有专家的分配概率和使用频率乘积的加权求和,用参数 α 来缩放损失。
import numpy as np
# 定义三个权重矩阵和对应的 top-k 矩阵
# 非常均衡、但是每个专家对每个token的处理高度类似
# 没有实现专家的特异化
weights_1 = np.array([
[0.34, 0.34, 0.32],
[0.34, 0.32, 0.34],
[0.34, 0.34, 0.32],
[0.32, 0.34, 0.34]
])
topk_1 = np.array([
[1, 1, 0],
[1, 0, 1],
[1, 1, 0],
[0, 1, 1]
])
# 每个专家都有被用到,也实现了一定的特异化
weights_2 = np.array([
[0.6, 0.25, 0.15],
[0.4, 0.4, 0.2],
[0.3, 0.6, 0.1],
[0.04, 0.06, 0.9]
])
topk_2 = np.array([
[1, 1, 0],
[1, 1, 0],
[1, 1, 0],
[0, 1, 1]
])
# 不均衡,只有专家1和专家2被使用
weights_3 = np.array([
[0.6, 0.25, 0.15],
[0.4, 0.4, 0.2],
[0.3, 0.6, 0.1],
[0.9, 0.06, 0.04]
])
topk_3 = np.array([
[1, 1, 0],
[1, 1, 0],
[1, 1, 0],
[1, 1, 0]
])
# 定义计算 Pi * fi 的函数
def calculate_aux_loss(weights, topk):
Pi = weights.mean(axis=0) # 计算纵向均值 Pi
fi = topk.mean(axis=0) # 计算纵向均值 fi
Pi_fi = Pi * fi # 计算 Pi * fi
return Pi_fi.sum() # 返回 aux_loss
# 计算三个 aux_loss
aux_loss_1 = calculate_aux_loss(weights_1, topk_1)
aux_loss_2 = calculate_aux_loss(weights_2, topk_2)
aux_loss_3 = calculate_aux_loss(weights_3, topk_3)
aux_loss_1, aux_loss_2, aux_loss_3输出结果为:
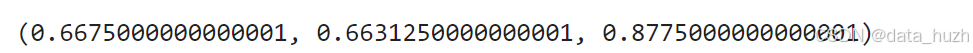





















 768
768

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








