曼哈顿距离简介

最新推荐文章于 2025-07-03 20:59:16 发布
转载 最新推荐文章于 2025-07-03 20:59:16 发布 · 2.2k 阅读 · 1 ·
CC 4.0 BY-SA版权
原文链接：https://blog.youkuaiyun.com/djstavaV/article/details/112261780
文章标签：

#曼哈顿距离简介

这篇文章深入浅出地介绍了曼哈顿距离的概念，源于曼哈顿岛的街道布局，用于二维和多维空间中的距离计算。通过实例解析了其公式并展示了与欧几里得距离的区别。

前言

维基百科上给的定义如下：

计程车几何(Taxicab geometry)或曼哈顿距离(Manhattan distance or Manhattan length)或方格线距离是由十九世纪的赫尔曼·闵可夫斯基所创辞汇，为欧几里得几何度量空间的几何学之用语，用以标明两个点上在标准坐标系上的绝对轴距之总和。

想象你在曼哈顿，要从一个十字路口开车到另外一个十字路口，实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源，曼哈顿距离也称为城市街区距离。

在上图中，绿线是欧几里得距离，红线是曼哈顿距离，蓝线和黄线是等价的曼哈顿距离。

二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离为：

d = | x1 - x2 | + |y1 - y2|

两个n维向量a(x11,x12,…,x1k)与 b(x21,x22,…,x2k)间的曼哈顿距离为：

 

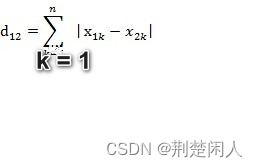
本文转自：曼哈顿距离简介_迷途小书童的Note的博客-优快云博客

 

 

【DL经典回顾】距离度量大汇总（2-曼哈顿距离(Manhattan Distance)）
悦学共鸣，温柔以待，汇聚光芒，共同成长
04-03 1861
曼哈顿距离（Manhattan Distance），也被称为L1距离或城市街区距离，是度量两点在标准坐标系上的绝对轴距离总和。本博客重点介绍这个距离度量方法。
算法 {曼哈顿距离}
qq_66485519的博客
04-29 739
1
曼哈顿距离（Manhattan Distance ）详解
热门推荐
岂曰无衣，与子同袍
07-15 3万+
概念 曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。 ——引用自百度 简析 就曼哈顿距离的概念来说，只能上、下、左、右四个方向进行移动，而且两点之间的曼哈顿距
曼哈顿距离（Manhattan Distance ）
qq_40723205的博客
10-21 1万+
曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离 就曼哈顿距离的概念来说，只能上、下、左、右四个方向进行移动，而且两点之间的曼哈顿距离是两点之间的最短距离（在只能向上...
曼哈顿距离
m0_73611175的博客
07-13 914
曼哈顿距离定义为在一个N维向量空间中，两个点之间的距离为它们在各个坐标轴上差值的绝对值之和。对于两个点 和，曼哈顿距离 D 的计算公式为：曼哈顿距离是一种简单有效的距离度量方法，特别适合在网格状或高维数据场景中使用。它的计算简单且易于理解，在很多实际应用中都有重要的作用。
精选资源
leetcode曼哈顿距离-computational-geometry:计算几何
06-30
曼哈顿距离 定义为 Math.abs(x2-x1) + Math.abs(y2-y1)。 切比雪夫距离 众所周知，给定点 (x, y) 并且您需要计算它们之间的曼哈顿距离 而不是使用 |x1-x2|+|y1-y2| 您可以先将所有点 (x, y) 转换为 (x+y, xy) 并且...
腐蚀&膨胀 曼哈顿距离
07-26
#### 二、曼哈顿距离简介 **曼哈顿距离**是一种度量两个点之间距离的方法，其定义为两点各坐标差的绝对值之和。例如，在二维空间中，若点A(x1,y1)和点B(x2,y2)，则它们之间的曼哈顿距离为| x1 - x2 | + | y1 - y2 |...
解释“欧几里得距离、曼哈顿距离和切比雪夫距离”
再来一下！
07-03 403
欧几里得距离（Euclidean Distance）、曼哈顿距离（Manhattan Distance）和切比雪夫距离（Chebyshev Distance）是三种常用的衡量两个点之间距离的方法。
Java实现 LeetCode 789 逃脱阻碍者（曼哈顿距离）
01-08
每一回合，你和阻碍者们可以同时向东，西，南，北四个方向移动，每次可以移动到距离原位置1个单位的新位置。 如果你可以在任何阻碍者抓住你之前到达目的地（阻碍者可以采取任意行动方式），则被视为逃脱成功。如果你...
曼哈顿距离（Manhattan Distance）
weixin_59167988的博客
09-26 1898
曼哈顿距离（Manhattan Distance）——两点在南北方向上的距离加上在东西方向上的距离在平面上，坐标(x1,y1)的i点与坐标(x2,y2)的j点的曼哈顿距离为 ： d(i,j)=|x1-x2|+|y1-y2|. 输入一个n，输出n阶菱形。n是奇数。 例如n = 9时： 找到中心点与n的关系：中心点用n表示为（n/2，n/2），将与中心点距离小于n/2的点用" * "表示，其他地方用空格表示
曼哈顿距离转化
最新发布
09-30
提供的引用内容未提及曼哈顿距离转化的方法和原理。曼哈顿距离本身是一种用于测量两个点在多维空间中的距离的距离度量方法，得名于曼哈顿的街区布局，交叉点的距离通常通过水平和垂直路线测量[^1]。 一般而言，曼哈顿距离在二维空间中，对于两点 \(P_1(x_1,y_1)\) 和 \(P_2(x_2,y_2)\)，其计算公式为 \(d = |x_1 - x_2|+|y_1 - y_2|\)。在多维空间中，若有两点 \(A=(a_1,a_2,\cdots,a_n)\) 和 \(B=(b_1,b_2,\cdots,b_n)\)，曼哈顿距离 \(d=\sum_{i = 1}^{n}|a_i - b_i|\) 。 对于曼哈顿距离的转化，从原理上可能是为了适应特定的应用场景或算法需求。例如在某些机器学习算法中，可能需要将曼哈顿距离转化为一种更易于计算或比较的形式。一种常见的转化方式是归一化，原理是将距离值映射到一个特定的区间，如 \([0,1]\) ，方法可以使用最小 - 最大归一化，公式为 \(d_{normalized}=\frac{d - d_{min}}{d_{max}-d_{min}}\) ，其中 \(d\) 是原始的曼哈顿距离，\(d_{min}\) 和 \(d_{max}\) 分别是数据集中曼哈顿距离的最小值和最大值。 ```python import numpy as np def manhattan_distance(point1, point2): return np.sum(np.abs(np.array(point1) - np.array(point2))) def min_max_normalization(distance, min_distance, max_distance): return (distance - min_distance) / (max_distance - min_distance) # 示例数据 point_a = [1, 2, 3] point_b = [4, 5, 6] # 计算曼哈顿距离 distance = manhattan_distance(point_a, point_b) # 假设已知最小和最大距离 min_dist = 0 max_dist = 10 # 归一化曼哈顿距离 normalized_distance = min_max_normalization(distance, min_dist, max_dist) print("原始曼哈顿距离:", distance) print("归一化后的曼哈顿距离:", normalized_distance) ```
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值