计算机中浮点数加法运算

十进制浮点数加法

首先以手工过程将科学计数法表示的两个十进制数相加：

9.999*10^1 + 1.610 * 10^-1。假设有效位只有4个十进制，且指数为两个十进制数位。

步骤1：为了能让两数相加，我们需对指数较小的小数点进行调整，使1.610 * 10^-1的指数项较大的指数对齐。

1.610 * 10^-1   =  0.1610 * 10^0 = 0.01610 * 10^1

最后边的形式是我们需要的。因为其指数和较大的数9.999*10^1的指数相同。因此，第一步要将较小数的有效位右移，直到其指数和较大数的指数相同。由于我们只能表示4位十进制，故移位后得到的数为

0.016 * 10^1

步骤2：将有效位相加

 9.999
+0.016
——————
10.015

和为10.015*10^1

步骤3：因为和不是规格化的科学记数法表示，因此需要调整：

10.015*10^1 = 1.0015*10^2

因此，在加法后可能需要对和进行移位，使其变为规格化形式，同时相应地调整指数。这个例子中是右移，但如果一个数为正，一个数为负数，则和可能会有许多前导0，从而需要左移。无论指数是增加还是减少，都需要检查上溢或者下溢，必须保证指数能够被固定位数的指数字段所表示。

步骤4：因为我们假设有效位只有4位十进制(不包括符号位)，所以需要对结果进行舍入。如：

1.0015*10^2

舍入为4位的十进制数

1.002*10^2

因为小数点后边第4位的数在5和9之间。注意，如果舍入有误，如将1加到了一串9上，则和不能再被规格化，需要再次执行步骤3。

总结：

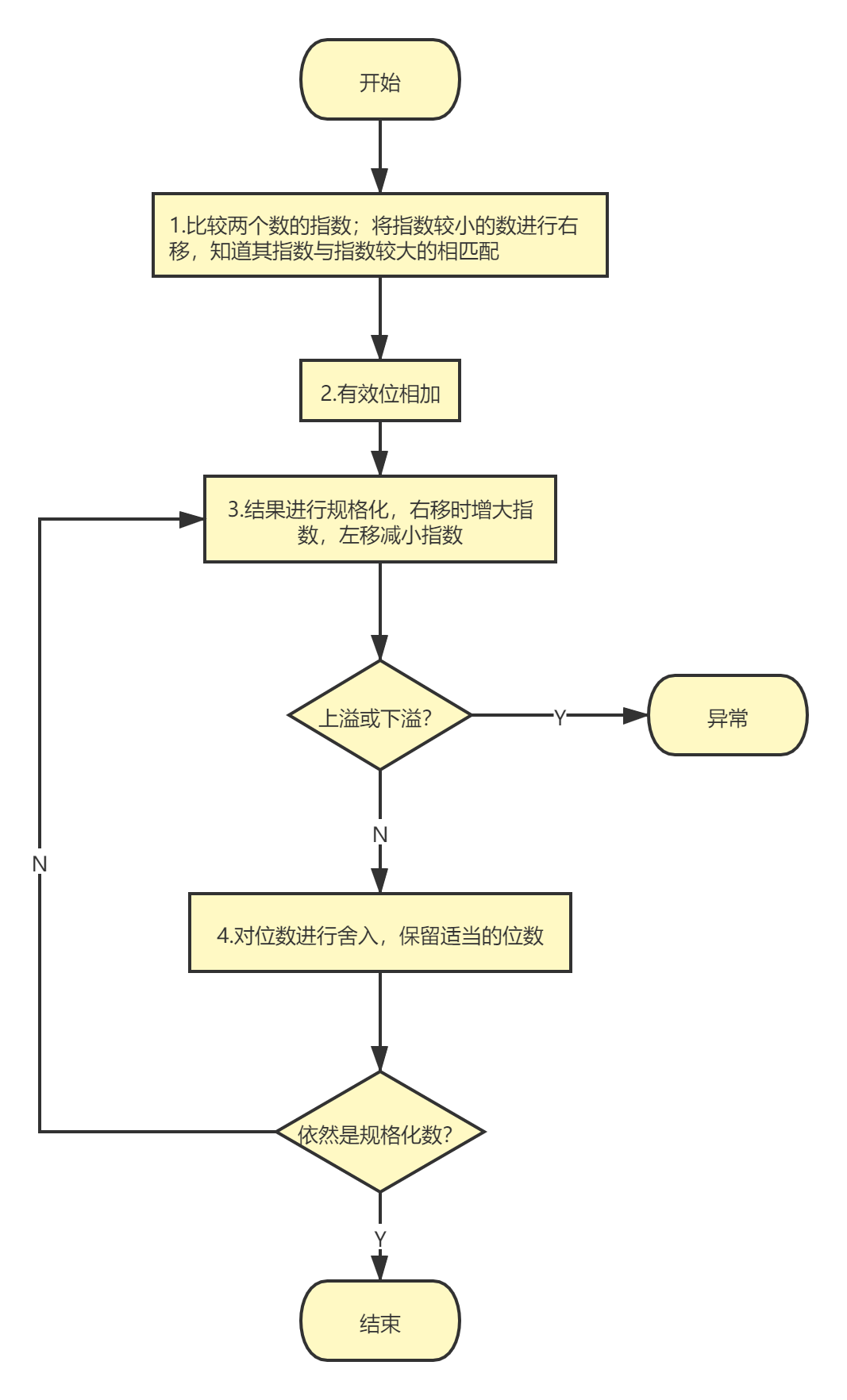
二进制浮点数加法

尝试将0.5(十进制)和-0.4375(十进制)用二进制相加

首先，看一下这两个数用规格化科学计数法表示的二进制形式，假设保持4位精度：

 

0.5(十进制) = 1/2  十进制      = 1/(2^1) 十进制    = 0.1 二进制        =0.1 * 2^0 二进制     = 1.000 * 2^-1 二进制
-0.4375(十进制) = -7/16 十进制   = -7/(2^4) 十进制  = -0.0111 二进制  = -0.011*2^0 二进制   = -1.110*2^-2 二进制

步骤1：指数较小的数(-1.11*2^-2  二进制)的有效右移，直到其指数和较大数的指数相匹配：

-1.110* 2^-2 = -0.111*2^-1

步骤2：将有效位相加

-1.110 * 2^-1   +  (-0.111* 2^-1) = 0.001 * 2^-1  二进制

步骤3：将和规格化，并检查上溢和下溢：

0.001 * 2^-1 = 0.010 * 2^-2 = 0.100 * 2^-3 = 1.000*2^-4

127≥-4≥-126 ,没有上溢和下溢。（带偏差的指数为-4+127，即123，其在最小的指数1和最大的指数254之间(未保留的带偏差的指数)。）

步骤4：舍入和：

1.000 * 2^-4 二进制

这个和正好用4位表示，故不需要再舍入，然后

1.000*2^-4 = 0.0001000=0.0001 二进制
=1/(2^4) = 1/16 = 0.0625 十进制