最大子数组和

目录

题目

核心思想

运行过程

 代码

验证

算法特点

理解

---

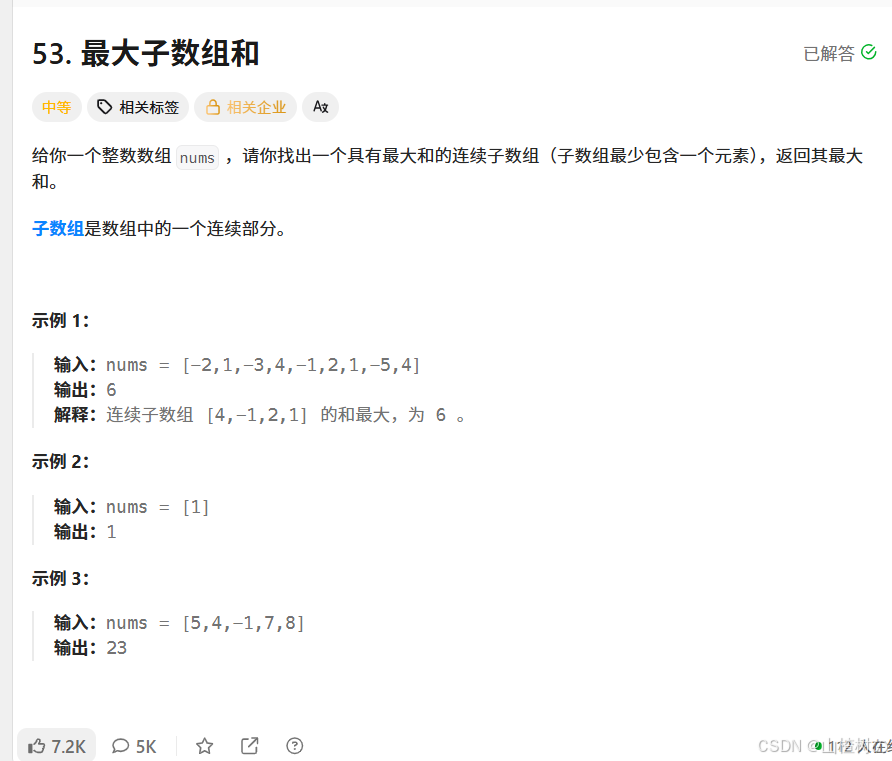
题目

 Kadane算法（动态规划解法），用于求解最大子数组和问题。（要求时间复杂度为O(n)）

核心思想

维护两个变量：

• sum：当前考虑的子数组的和

• ans：到目前为止找到的最大和

运行过程

1. 初始化：

   • ans = nums[0]（不能初始化为0，因为数组可能全为负数）

   • sum = 0

2. 遍历数组：

   • 对于每个数字 num：

     • 如果 sum > 0：说明当前累加的子数组还有价值，继续累加 sum += num

     • 如果 sum <= 0：说明当前累加的子数组只会拖累后面的元素，不如重新开始 sum = num

     • 每次更新后，用 ans 记录最大值

3. 返回结果：ans 就是最大子数组和

 代码

var maxSubArray = function(nums) {
    let ans = nums[0];
    let sum = 0;
    for(const num of nums) {
        if(sum > 0) {
            sum += num;
        } else {
            sum = num;
        }
        ans = Math.max(ans, sum);
    }
    return ans;
};

• 动态规划的是首先对数组进行遍历，当前最大连续子序列和为 sum，结果为 ans
• 如果 sum > 0，则说明 sum 对结果有增益效果，则 sum 保留并加上当前遍历数字
• 如果 sum <= 0，则说明 sum 对结果无增益效果，需要舍弃，则 sum 直接更新为当前遍历数字
• 每次比较 sum 和 ans的大小，将最大值置为ans，遍历结束返回结果
• 时间复杂度：O(n)

验证

数组: [-2, 1, -3, 4, -1, 2, 1, -5, 4]

步骤   元素   sum>0?    操作                sum值     ans值    说明
---   ----   ------    ----------------    -----    -----    ----
0      -2    否        重新开始: sum=-2       -2       -2      ← ans初始为-2
1       1    否(sum=-2)重新开始: sum=1         1        1      负数的sum只会拖累，重新开始
2      -3    是(sum=1) 累加: sum=1-3=-2       -2        1      正数sum继续累加，但变小了
3       4    否(sum=-2)重新开始: sum=4         4        4      负数sum拖累，重新开始
4      -1    是(sum=4) 累加: sum=4-1=3        3        4      继续累加
5       2    是(sum=3) 累加: sum=3+2=5        5        5      累加后超过当前ans
6       1    是(sum=5) 累加: sum=5+1=6        6        6      达到最大值
7      -5    是(sum=6) 累加: sum=6-5=1        1        6      累加但变小了
8       4    是(sum=1) 累加: sum=1+4=5        5        6      最后累加

最终结果: ans = 6

算法特点

• 时间复杂度：O(n)，只需遍历一次数组

• 空间复杂度：O(1)，只用了常数空间

• 适用性：可以处理包含负数的数组

理解

sum > 0 的判断实际上是问："当前累加的子数组是否对后续元素有正面贡献？"

• 如果 sum > 0，加上后面的元素有可能变得更大

• 如果 sum <= 0，加上后面的元素只会更小或不变，不如重新开始

一种贪心思想与动态规划的结合，每次只保留对后续有贡献的部分。