【论文阅读】GRAPH ATTENTION NETWORKS

摘要

本文提出了一种新的基于图结构数据的神经网络结构——图注意力网络(GATs)，不同于先前一些基于谱域的图神经网络，通过使用masked self-attentional layers 解决了图卷积网络（GCN）方面的一些缺点。通过堆叠层可以获得邻域节点的特征值，这样我们可以（隐式地）为邻域中的不同节点指定不同的权重，而不需要任何形式的复杂的矩阵运算（如转置），也不需要了解图本身的结构。本文同时解决了GCN的几个关键挑战，并使模型同时适用于Inductive和Transductive问题。我们的GAT模型已经在四个已建立的Inductive和Transductive基准上取得或匹配了最先进的结果：Cora、Citeseer和Pubmed引文网络数据集，以及蛋白质相互作用数据集（其中测试图在训练期间是看不见的）。

如何理解 inductive learning 与 transductive learning?

1 引言

由于注意力机制在RNN与CNN中都取得了不错的效果，基于此作者在此篇文章提出了图注意力机制。此方法的优点在于可以处理任意大小输入的问题，并且关注最具有影响能力的输入。

在摘要中作者说明了，本文的attention计算的目的是为每个节点邻域中的节点分配不同的权重，也就是attention是用来关注那些作用比较大的节点，而忽视一些作用较小的节点。

本文提出的GAT模型具有以下三个特点：

1. attention机制计算效率高，为每一个节点和其每个邻域节点计算attention可以并行进行。
2. 通过指定任意的权重给邻域节点，这个模型可以处理拥有不同度的节点，也就是说，无论一个节点连接多少个邻域节点，这个模型都能按照规则指定权重。
3. 该模型直接适用于inductive learning problem，包括将模型推广到完全不可见图的任务。

2 GAT结构

在这个模块，作者提出了一种图注意力层，通过堆叠这个层来实现图注意力机制。通过与之前神经图处理领域的方法进行比较，阐述其优势及局限性。

2.1 图注意力层（GRAPH ATTENTIONAL LAYER）

首先要描述一个单层的图注意力层，作为一个单独的网络层被用于GAT框架中。

2.1.1 输入输出

上述网络层的输入是一组节点特征的集合：

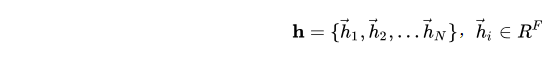
其中，$N$是节点数，$F$是每个节点中的特征数。

网络层的输出是一组新的节点特征的集合：

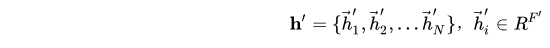
其中，节点数$N$不变，节点的特征数可变化为$F^{\prime }$。

2.1.2 特征提取与注意力机制

为了将输入特征转换为高维特征（增维）以获得足够的表达能力，至少需要一个可学习的线性变换。因此，为每个节点训练一个权值矩阵$W\in R^{F\times F^{\prime }}$，这个权值矩阵就是输入特征与输出特征的直接关系。

然后，对每个节点进行共享的注意力机制 $a$：$R^{F^{\prime }}$