Graph attention works
个人理解,gnn这类图神经网络思想就是学习到每个节点的特征对于其相邻更远节点的影响,越近的节点影响越大。 通过这种影响的传播,从而获取到整个拓扑图的结构性的信息。
具体思想的核心是通过拉普拉斯矩阵可以对图信息进行特征分解的特点把该公式定义为图卷积操作,同时图卷积的出现也填补了神经网络获取拓扑图类型特征的空白。
GCN
CNN处理的图像或者视频数据中像素点(pixel)是排列成成很整齐的矩阵,论文提到
Euclidean Structure。
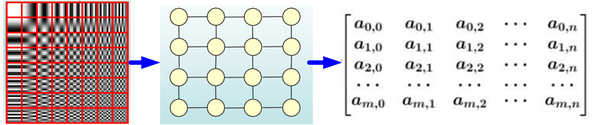
非Euclidean Structure的网络结构,也是图论抽象意义的拓扑图。

Graph Convolutional Network中的Graph是指数学(图论)中的用顶点和边建立相应关系的拓扑图。
提取拓扑图空间特征的两种方式:
(1) vertex domain
(2) spectral domain
这种思路就是希望借助图谱的理论来实现拓扑图上的卷积操作。
图谱理论简单的概括就是借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质。
为什么可以借助图谱理论进行GCN? 涉及大量数学推导。
拉普拉斯变换后的矩阵是正定对称矩阵,可以进行特征分解(谱分解)。
对于图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E), 其Laplacian 矩阵的定义为
L
=
D
−
A
L=D-A
L=D−A ,其中
L
L
L是Laplacian 矩阵
D
D
D 是顶点的度矩阵(对角矩阵),对角线上元素依次为各个顶点的度,
A
A
A是图的邻接矩阵。

常用的拉普拉斯矩阵实际有三种:
No.1
L
=
D
−
A
L=D-A
L=D−A 定义的Laplacian 矩阵更专业的名称叫Combinatorial Laplacian
No.2
L
s
y
s
=
D
−
1
/
2
L
D
−
1
/
2
L^{sys}=D^{-1/2}LD^{-1/2}
Lsys=D−1/2LD−1/2 定义的叫Symmetric normalized Laplacian (GCN)
No.3
L
r
w
=
D
−
1
L
L^{rw}=D^{-1}L
Lrw=D−1L 定义的叫Random walk normalized Laplacian
首次将深度学习里卷积操作引入图数据里的方法GCN是Thomas Kpif于2017年在论文Semi-supervised classification with graph convolutional networks提出的,在他的博客里对模型解释非常清楚。
GCN网络的每一层结构很清晰:
f ( H ( l ) , A ) = σ ( D ^ − 1 2 A ^ D ^ − 1 2 H ( l ) W ( l ) ) f(H^{(l)}, A) = \sigma\left( \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}\right) f(H(l),A)=σ(D^−21A^D^−21H(l)W(l))
Graph attention works
Graph attention networks在基于GCN模型将深度学习处理图模型的基础上引入attention思想去计算每个节点的邻居节点对它的权重,从而达到从局部信息可以获取到整个网络整体信息却无需提前知道整个网络的结构,同时通过堆叠这些隐藏自注意层能够获取临近点的特征,从而避免大量矩阵运算,计算高效。
Gat Architecture
features输入
输入是一组顶点特征 h = h ⃗ 1 , h ⃗ 2 , … , h ⃗ N , h ⃗ i ∈ R F {\mathbf{h}} = { \vec{h}_1, \vec{h}_2, …, \vec{h}_N }, \vec{h}_i \in \mathbb{R}^F h=h1,h2,…,hN,hi∈RF, 其中 N N N是顶点数, F F F 是每个顶点的特征数。这个层会生成一组新的顶点特征, h ’ = h ⃗ ’ 1 , h ⃗ ’ 2 , … , h ⃗ ’ N , h ⃗ ’ i ∈ R F ’ {\mathbf{h}’} = { \vec{h}’_1, \vec{h}’_2, …, \vec{h}’_N}, \vec{h}’_i \in \mathbb{R}^{F’} h’=h’1,h’2,…,h’N,h’i∈RF’作为输出。
计算相互关注
为了在将输入特征变换到高维特征时获得充足的表现力,至少需要一个可学习的线性变换。为了到达这个目的,每个顶点都会使用一个共享参数的线性变换,参数为
W
∈
R
F
’
×
F
{\mathbf{W}} \in \mathbb{R}^{F’ \times F}
W∈RF’×F,然后在每个顶点上做一个 self-attention ——一个共享的attention机制
a
:
R
F
’
×
R
F
’
→
R
a : \mathbb{R}^{F’} \times \mathbb{R}^{F’} \rightarrow \mathbb{R}
a:RF’×RF’→R :
e
i
j
=
a
(
W
h
⃗
i
,
W
h
⃗
j
)
\ e_{ij} = a(\mathbf{W} \vec{h}_i, \mathbf{W} \vec{h}_j)
eij=a(Whi,Whj)
表示顶点 j 的特征对顶点 i 的重要性(importance)。在一般的公式中,模型可以使每个顶点都注意其他的每个顶点,扔掉所有的结构信息。作者使用 mask attention 使得图结构可以注入到注意力机制中——我们只对顶点 相邻的点计算attention coefficient。为了让系数在不同的顶点都可比,我们对所有的 j 使用 softmax 进行了归一化:
α i j = s o f t m a x j ( e i j ) = exp e i j ∑ k ∈ N i exp e i k (2) \tag{2} \alpha_{ij} = \mathrm{softmax}_j (e_{ij}) = \frac{\exp{e_{ij}}}{\sum_{k \in \mathcal{N}_i} \exp{e_{ik}}} αij=softmaxj(eij)=∑k∈Niexpeikexpeij(2)
注意力机制 a 是一个单层的前向传播网络,参数为权重向量 a ⃗ ∈ R 2 F ’ \vec{\text{a}} \in \mathbb{R}^{2F’} a∈R2F’,使用LeakyReLU作为非线性层(斜率α=0.2)。整个合并起来,注意力机制计算出的分数(如图1左侧所示)表示为:
α i j = exp ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∥ W h ⃗ j ] ) ) ∑ k ∈ N i exp ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∥ W h ⃗ k ] ) ) (3) \tag{3} \alpha_{ij} = \frac{ \exp{ ( \mathrm{LeakyReLU} ( \vec{\text{a}}^T [\mathbf{W} \vec{h}_i \Vert \mathbf{W} \vec{h}_j ] ))}}{\sum_{k \in \mathcal{N_i}} \exp{(\mathrm{LeakyReLU}(\vec{\text{a}}^T [\mathbf{W} \vec{h}_i \Vert \mathbf{W} \vec{h}_k]))}} αij=∑k∈Niexp(LeakyReLU(aT[Whi∥Whk]))exp(LeakyReLU(aT[Whi∥Whj]))(3)
得到归一化的分数后,使用归一化的分数计算对应特征的线性组合,作为每个顶点最后的输出特征(最后可以加一个非线性层,σ)
h ⃗ ’ i = σ ( ∑ j ∈ N i α i j W h ⃗ j ) (4) \tag{4} \vec{h}’_i = \sigma(\sum_{j \in \mathcal{N}_i} \alpha_{ij} \mathbf{W} \vec{h}_j) h’i=σ(j∈Ni∑αijWhj)(4)
为了稳定 self-attention 的学习过程,作者使用multi-head attention 来扩展注意力机制。特别地,K 个独立的 attention 机制执行上面 这样的变换,然后他们的特征连(concatednated)在一起,就可以得到如下的输出:
h
⃗
’
i
=
∥
k
=
1
K
σ
(
∑
j
∈
N
i
α
i
j
k
W
k
h
⃗
j
)
(5)
\tag{5} \vec{h}’_i = \Vert^{K}_{k=1} \sigma(\sum_{j \in \mathcal{N}_i} \alpha^k_{ij} \mathbf{W}^k \vec{h}_j)
h’i=∥k=1Kσ(j∈Ni∑αijkWkhj)(5)
其中 ∥ 表示concatenation,
α
i
j
k
\alpha^k_{ij}
αijk是通过第 k 个注意力机制 (
a
k
a^k
ak) 计算出的归一化的注意力分数,Wk 是对应的输入线性变换的权重矩阵。注意,在这里,最后的返回输出 h′,每个顶点都会有 KF′ 个特征(不是 F′ )。特别地,如果网络的最后一层使用 multi-head attention,concatenation 就不再可行了,论文使用 averaging,并且延迟使用最后的非线性层(分类问题通常是 softmax 或 sigmoid ):
h
⃗
’
i
=
σ
(
1
K
∑
k
=
1
K
∑
j
∈
N
i
α
i
j
k
W
k
h
⃗
j
)
\vec{h}’_i = \sigma(\frac{1}{K} \sum^K_{k=1} \sum_{j \in \mathcal{N}_i} \alpha^k_{ij} \mathbf{W}^k \vec{h}_j)
h’i=σ(K1k=1∑Kj∈Ni∑αijkWkhj)
实验数据
Transductive learning
在cora数据集上使用一个两层的GAT模型,第一层包含K=8个attention head,计算得到F′=8个特征(总共64个特征),之后接一个指数线性单元(ELU)作为非线性激活函数,第二层用作分类:一个单个的attention head计算C个特征(其中C是类别的数量),之后用softmax激活。处理小训练集时,在模型上加正则化。
对比结果
代码解读
1*1 卷积的作用?
在吴恩达卷积神经网络课程2.5节提到对输入数据进行11卷积操作是一个很有影响力的操作,常用于三维的输入数据,通过设定11卷积核的个数改变数据第三维(通道数量)的大小。当然你也可以保持通道数的不变,那么1*1卷积就相当于给输入添加一层非线性的函数变换,从而让网络学习到更复杂的表示。
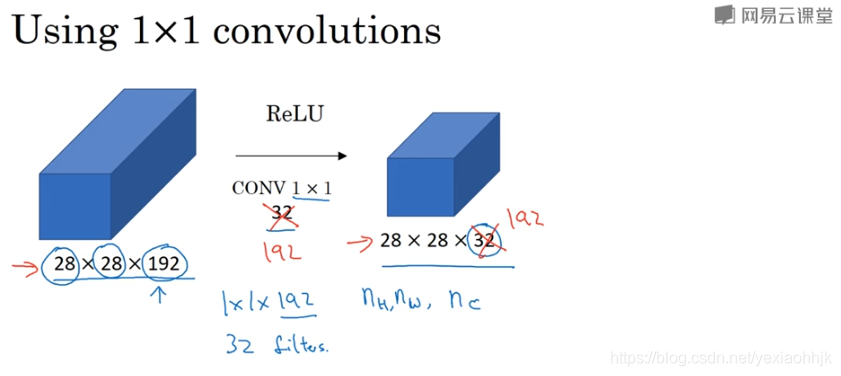 同样的,输入数据是二维的时候,
同样的,输入数据是二维的时候,1* 1的一维卷积作用也是类似的。
Tensorflow里函数为tf.layers.conv1d,tf.layers.conv2d。
conv1d的参数如下图所示:
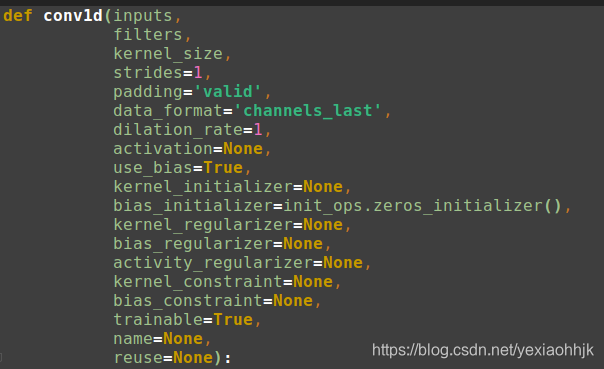
filters:过滤器个数,控制输出的大小。
kernel_size:卷积核大小。
self-attention
论文里关于GAT模型的计算任意两点注意力的系数实现如下,即上面的公式(3):
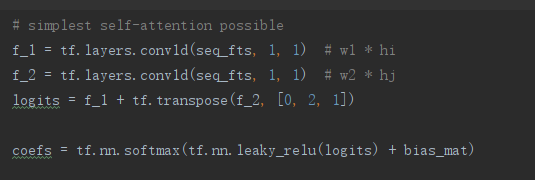
关于tf.layers.conv1d的函数解析 。
这个写法和论文的公式(3)貌似不一样,实际是简单的等价,这里聚合是把n*m的实体向量h通过一维卷积降n*1成1维后,然后利用加分的广播机制,计算任意两点的信息,作者的解释:
当我们这一层神经网络是单层的, [ W h ⃗ i ∥ W h ⃗ j ] [\mathbf{W} \vec{h}_i \Vert \mathbf{W} \vec{h}_j ] [Whi∥Whj] 可以分解成 [ W 1 h ⃗ i + W 2 h ⃗ j ] [\mathbf{W_{1}} \vec{h}_i + \mathbf{W_{2}} \vec{h}_j ] [W1hi+W2hj], 其中 W 1 W_{1} W1 与 W 2 W_{2} W2是两个独立参数。
W
1
h
⃗
i
W_{1}\vec{h}_{i}
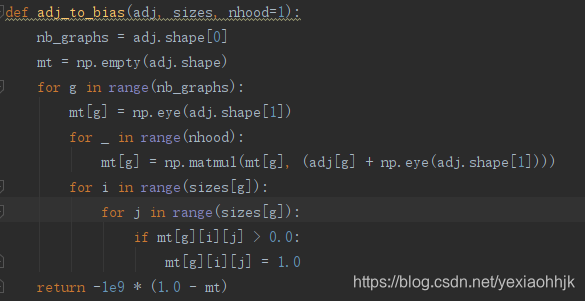
W1hi 我们就可以借助上面讲的卷积核大小为1的一维卷积conv1d去实现这个转换,代码里f_1就是它的表示,但这里代码先实现是计算任意两点的相关系数,在加上bias_mat后即实现论文里说采用mask attention机制使得只有相邻两点的相关度系数会被计算。
bias_mat本质是一个将整个图的邻接矩阵转换后得到的二维矩阵,如果这i,j两点之间没有边,就被赋值无穷小,如果有边赋值为0,这样加上计算任意两点相关系数结果,就实现只计算图上相邻两点的相关性系数,这方法被论文称为 mask attention。








 本文探讨了图神经网络(GNN)的概念及其在图数据上的应用,详细介绍了图卷积网络(GCN)的工作原理,包括如何通过拉普拉斯矩阵进行特征分解,以及GCN如何填补神经网络在处理拓扑图特征的空白。此外,文章还深入分析了图注意力网络(GAT)的架构,展示了如何结合注意力机制和GCN模型来更有效地处理图数据,尤其是在计算每个节点的邻居节点权重方面。
本文探讨了图神经网络(GNN)的概念及其在图数据上的应用,详细介绍了图卷积网络(GCN)的工作原理,包括如何通过拉普拉斯矩阵进行特征分解,以及GCN如何填补神经网络在处理拓扑图特征的空白。此外,文章还深入分析了图注意力网络(GAT)的架构,展示了如何结合注意力机制和GCN模型来更有效地处理图数据,尤其是在计算每个节点的邻居节点权重方面。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








