Halcon算子扩展——获取矩形4个角点

原创已于 2025-08-20 09:57:32 修改 · 574 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #经验分享 #笔记

于 2025-08-16 15:08:21 首次发布

Halcon 专栏收录该内容

6 篇文章

订阅专栏

在视觉测量与定位的应用中，我们经常会遇到这样的场景。通过二值化以及形态学计算，我们获得了一些独立的区域，想要获取这些区域对应最小包围矩形的4个角点。对于某个区域，利用smallest_rectangle2算子，可以轻松获得其中心、角度，以及两个半长度。根据矩形长边方向的不同，计算4分角点的过程也会有所差异。

为了获得统一且一致的效果。本文给出了2种可行的方法，并且已经进行封装测试，可以直接运行使用。以供各位读者参考学习。

1.原理介绍

方法1：使用方向向量

1.1矩形长轴与垂直方向呈现锐角

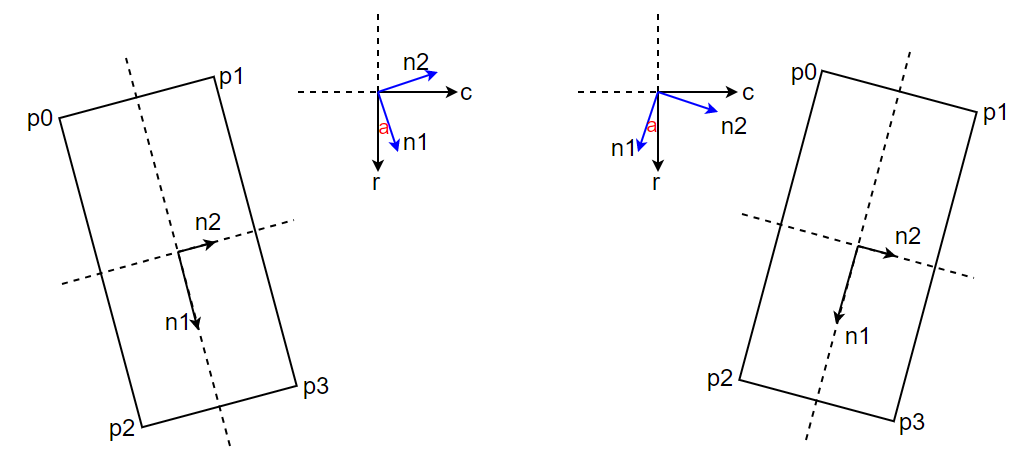
如上图所示，左有两侧矩形的长轴角度分别为-70°和70°。假设长轴和短轴的方向向量分别为n_{1} 和n_{2} 。并且假设长轴方向向量与垂直方向夹角的绝对值为 $\theta$ 。易知两侧的符号函数sgn(x)取值分别为-1和1。现在我们可以写出左右两侧矩形方向向量的表达式：

左侧矩形的方向向量为：

$\left\{\begin{matrix} n_{1} = (\cos \theta , \sin \theta)\\ n_{2} = (-\sin \theta , \cos \theta) \end{matrix}\right.$

右侧矩形的方向向量为：

$\left\{\begin{matrix} n_{1} = (\cos \theta , -\sin \theta)\\ n_{2} = (\sin \theta , \cos \theta) \end{matrix}\right.$

利用sgn(x)函数，将两者组合，可以写为：

$\left\{\begin{matrix} n_{1} = (\cos \theta , -sgn*\sin \theta)\\ n_{2} = (sgn*\sin \theta , \cos \theta) \end{matrix}\right.$

1.2矩形长轴与水平方向呈现锐角

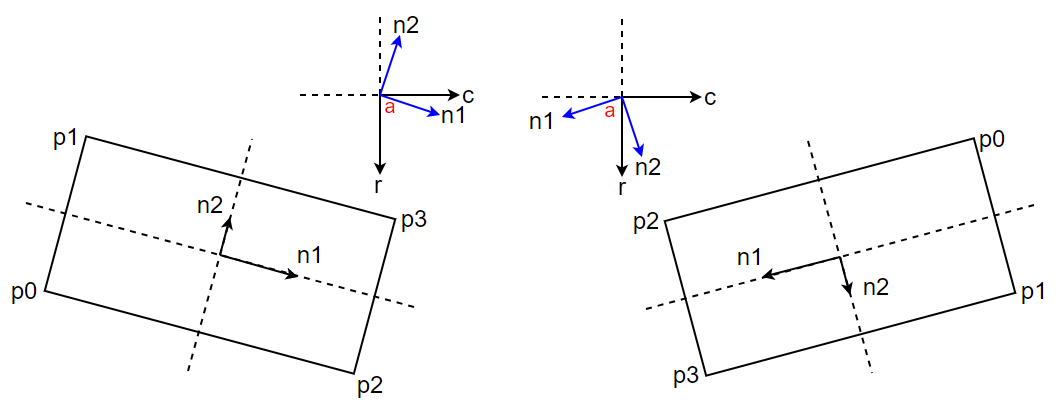
如上图所示，左有两侧矩形的长轴角度分别为-20°和20°。假设长轴和短轴的方向向量分别为n_{1} 和n_{2} 。并且假设长轴方向向量与垂直方向夹角的绝对值为 $\theta$ 。易知两侧的符号函数sgn(x)取值分别为-1和1。现在我们可以写出左右两侧矩形方向向量的表达式：

左侧矩形的方向向量为：

$\left\{\begin{matrix} n_{1} = (\cos \theta , \sin \theta)\\ n_{2} = (-\sin \theta , \cos \theta) \end{matrix}\right.$

右侧矩形的方向向量为：

$\left\{\begin{matrix} n_{1} = (\cos \theta , -\sin \theta)\\ n_{2} = (\sin \theta , \cos \theta) \end{matrix}\right.$

利用sgn(x)函数，将两者组合，可以写为：

$\left\{\begin{matrix} n_{1} = (\cos \theta , -sgn*\sin \theta)\\ n_{2} = (sgn*\sin \theta , \cos \theta) \end{matrix}\right.$

可见1.1和1.2中最终的形式一样。这是由于角度大小统一设置为矩形长轴与垂直方向的夹角。

方法2：使用仿射变换

假设我们将矩形旋转，使得其长轴方向置于水平，则容易获得其4个角点的坐标。由于旋转角度是已知的，因此我们可以将刚才获得的4个角点坐标变换回去。此时，便可得到原先的4个角点的坐标。不过，需要注意各角点的顺序。

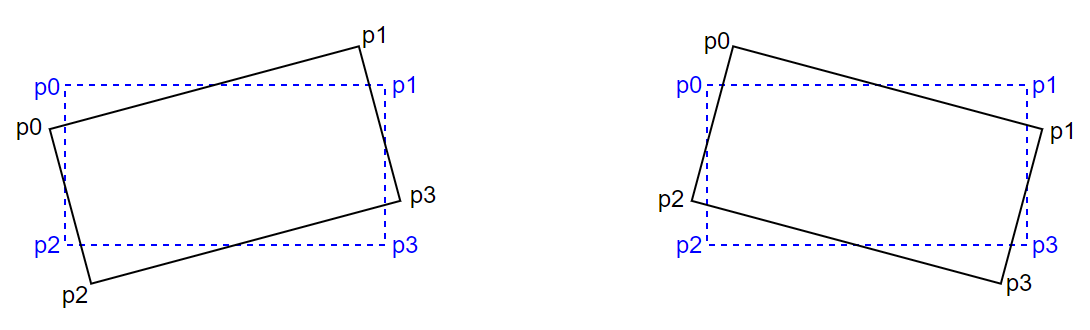
如上图所示，左右两侧倾斜矩形的角度分别为20°和-20°。对应的符号函数sgn(x)的取值分别为1和-1。

矩形变换前后的4各角点坐标都为(p0,p1,p2,p3)。为了与方法1中输出结果的角点顺序一致，需要将方法2输出结果重新排序。

左侧重新排序后，输出结果为(p2,p4,p1,p3)。

右侧重新排序后，输出结果为(p3,p1,p4,p2)。

2 代码脚本

2.1方法1

smallest_rectangle2(rt2, cur_Row, cur_Col, cur_Phi, cur_Len1, cur_Len2)
cur_Deg := deg(cur_Phi)
cur_Sgn := sgn(cur_Deg)
oft_AbsDeg := 90 - abs(cur_Deg) //与垂直方向的绝对角度差
oft_AbsRad := rad(oft_AbsDeg)
norm1 := [cos(oft_AbsRad), -cur_Sgn*sin(oft_AbsRad)]
norm2 := [cur_Sgn*sin(oft_AbsRad), cos(oft_AbsRad)]
LM_Row := cur_Row - norm2[0]*cur_Len2
LM_Col := cur_Col - norm2[1]*cur_Len2
LT_Row := LM_Row - norm1[0]*cur_Len1
LT_Col := LM_Col - norm1[1]*cur_Len1
LD_Row := LM_Row + norm1[0]*cur_Len1
LD_Col := LM_Col + norm1[1]*cur_Len1
RT_Row := LT_Row + norm2[0]*cur_Len2*2
RT_Col := LT_Col + norm2[1]*cur_Len2*2
RD_Row := LD_Row + norm2[0]*cur_Len2*2
RD_Col := LD_Col + norm2[1]*cur_Len2*2
* TM_Row := LT_Row + norm2[0]*cur_Len2
* TM_Col := LT_Col + norm2[1]*cur_Len2
* DM_Row := LD_Row + norm2[0]*cur_Len2
* DM_Col := LD_Col + norm2[1]*cur_Len2

* gen_cross_contour_xld(Cross_LM, LM_Row, LM_Col, 50, cur_Phi)
gen_cross_contour_xld(Cross_LT, LT_Row, LT_Col, 50, cur_Phi)
gen_cross_contour_xld(Cross_LD, LD_Row, LD_Col, 50, cur_Phi)
gen_cross_contour_xld(Cross_RT, RT_Row, RT_Col, 50, cur_Phi)
gen_cross_contour_xld(Cross_RD, RD_Row, RD_Col, 50, cur_Phi)
* gen_cross_contour_xld(Cross_DM, DM_Row, DM_Col, 50, cur_Phi)
* gen_cross_contour_xld(Cross_TM, TM_Row, TM_Col, 50, cur_Phi)

rows := [LT_Row, RT_Row, LD_Row, RD_Row]
cols := [LT_Col, RT_Col, RD_Col, RD_Col]


stop()
return ()

2.2方法2

smallest_rectangle2(rt2, cur_Row, cur_Col, cur_Phi, cur_Len1, cur_Len2)
cur_Deg := deg(cur_Phi)
cur_Sgn := sgn(cur_Deg)
oft_AbsDeg := 90 - abs(cur_Deg) //与垂直方向的绝对角度差
oft_AbsRad := rad(oft_AbsDeg)

gen_rectangle2(rt1, cur_Row, cur_Col, 0, cur_Len1, cur_Len2)
rt1_Rows := [cur_Row - cur_Len2, cur_Row - cur_Len2, cur_Row + cur_Len2, cur_Row + cur_Len2]
rt1_Cols := [cur_Col - cur_Len1, cur_Col + cur_Len1, cur_Col - cur_Len1, cur_Col + cur_Len1]

hom_mat2d_identity(hom2d_I)
hom_mat2d_rotate(hom2d_I, cur_Phi, cur_Row, cur_Col, hom2d_rot)
affine_trans_point_2d(hom2d_rot, rt1_Rows, rt1_Cols, rt2_rows, rt2_cols)

* gen_cross_contour_xld(Cross_LT0, rt1_Rows[0], rt1_Cols[0], 50, 0)
* gen_cross_contour_xld(Cross_RT0, rt1_Rows[1], rt1_Cols[1], 50, 0)
* gen_cross_contour_xld(Cross_LD0, rt1_Rows[2], rt1_Cols[2], 50, 0)
* gen_cross_contour_xld(Cross_RD0, rt1_Rows[3], rt1_Cols[3], 50, 0)

Ids := [1,3,0,2]
if (cur_Deg < 0)
    Ids := [2,0,3,1]
endif

rows := rt2_rows[Ids]
cols := rt2_cols[Ids]
* gen_cross_contour_xld(Cross1, rows[0], cols[0], 50, cur_Phi)
* gen_cross_contour_xld(Cross2, rows[1], cols[1], 50, cur_Phi)
* gen_cross_contour_xld(Cross3, rows[2], cols[2], 50, cur_Phi)
* gen_cross_contour_xld(Cross4, rows[3], cols[3], 50, cur_Phi)

2.3方法调用

* get_rect2_corners1 (rt2_0, rows1, cols)
get_rect2_corners2 (rt2_0, rows, cols1)

读者可将上述两个方法封装为halcon函数，如上述代码所示进行调用。

3 输出结果

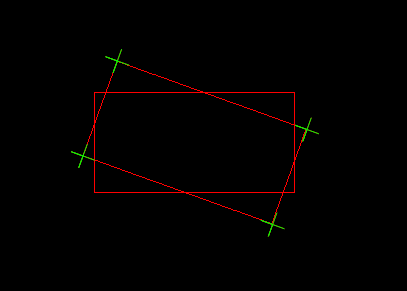
结果如上图所示，可见倾斜矩形各角点位置已经正确获得。