1.背景介绍
同态滤波算法将图像表示为照明反射模型,即图像亮度是照明与反射的乘积。作为一种频域滤波器,它认为图像中的低频分量对应照明部分,高频分量对应反射部分。因此,可以设计这样的滤波器:其对低频部分进行抑制,对高频部分增强。当图像应用此滤波器后,照明部分被减弱,纹理细节部分被增强。
2.原理介绍
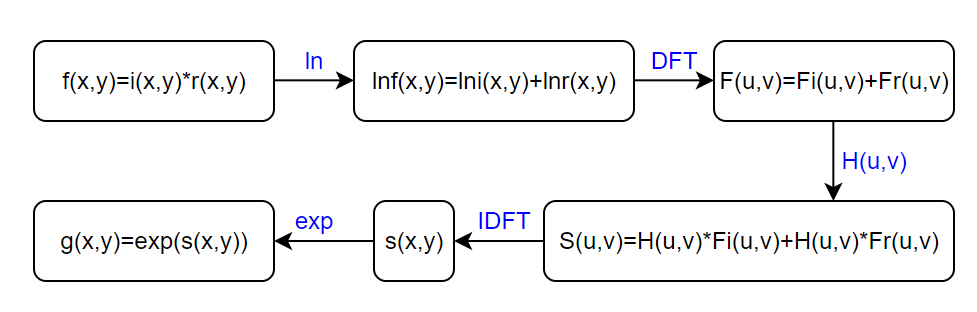
如上图所示,为算法的主要处理流程。
(1)将图像表示为照射分量与反射分量的乘积
(2)通过对数运算,将乘性分量转换为加性分量
(3)对上式进行傅里叶变换
(4)使用滤波器进行滤波
(5)对滤波结果进行傅里叶逆变换得到。则最终滤波结果图像为
3.同态滤波器介绍
3.1高斯高通滤波
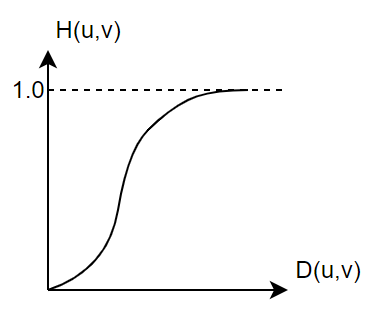
高斯高通滤波器函数表达式为
此滤波器,将抑制靠近0的低频分量,增强靠近1的高频分量。
3.2改进的高斯高通滤波
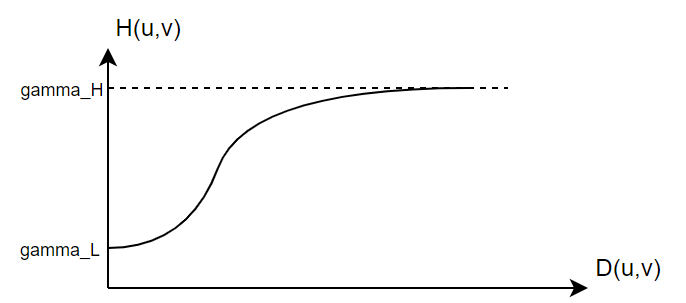
改进的高斯高通滤波器函数表达式为
其中,c表示高斯函数的陡峭程度(影响不大)。表示截至频率。
此滤波器,将抑制靠近的低频分量,增强靠近
的高频分量。
3.3巴特沃斯高通滤波
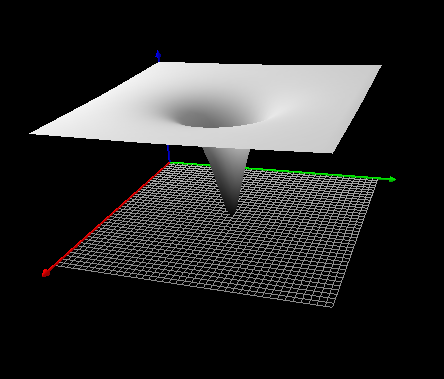
巴特沃斯高通滤波器的表达式为
其中,D(u,v)表示:频域中某点(u,v)到中心点的距离。为截至频率。
4.算法的halcon算子封装
4.1中心距离变换算子distance_transform_center
halcon中现有的距离变换算子distance_transform,计算的是区域内各点到图像边缘的距离。为了构造合适的滤波器形态,我们需要计算各点到图像中心的距离。
Rows := []
Cols := []
cur_Cs := [0:Img_Width-1]
for r:= 0 to Img_Height-1 by 1
cur_Rs := gen_tuple_const(Img_Width, r)
Rows := [Rows, cur_Rs]
Cols := [Cols, cur_Cs]
endfor
distance_pp(Rows, Cols, 0.5*Img_Height, 0.5*Img_Width, Dists)
gen_image_const(CenterDistanceImage, 'real', Img_Width, Img_Height)
set_grayval(CenterDistanceImage, Rows, Cols, Dists)
return ()4.2同态滤波算子homomorphic_filter
get_image_size(Img, Img_Width, Img_Height)
convert_image_type(Img, Img_f0, 'real')
log_image(Img_f0, Img_log0, 'e')
fft_generic(Img_log0, Img_fft0, 'to_freq', -1, 'sqrt', 'dc_center', 'complex')
gen_image_proto(Img, Img0_1, 1)
convert_image_type(Img0_1, Img_1, 'real')
if (filter_type == 'gauss1')
Sigma := paras[0]
gen_gauss_filter (gs, paras, paras, 0, 'n', 'dc_center', Img_Width, Img_Height)
sub_image(Img_1, gs, Highpass, 1, 0)
elseif(filter_type == 'gauss2')
gamma_H := paras[0]
gamma_L := paras[1]
c := paras[2]
D0 := paras[3]
distance_transform_center (Img_cd0, Img_Width, Img_Height)
pow_image(Img_cd0, H_D2, 2)
mult_factor := -c/(D0*D0)
scale_image(H_D2, H_scale0, mult_factor, 0)
exp_image(H_scale0, H_exp0, 'e')
sub_image(Img_1, H_exp0, H_sub0, 1, 0)
scale_image(H_sub0, Highpass, gamma_H - gamma_L, gamma_L)
elseif(filter_type == 'butterworth')
D0 := paras[0]
n1 := paras[1]
distance_transform_center (Img_cd0, Img_Width, Img_Height)
gen_image_proto(Img, H0, D0)
convert_image_type(H0, Img_D0, 'real')
div_image(Img_D0, Img_cd0, Img_div0, 1, 0) // D0/D
pow_image(Img_div0, Img_pow0, 2*n1) // (D0/D)^(2*n1)
add_image(Img_1, Img_pow0, Img_add0, 1, 0) // 1 + (D0/D)^(2*n1)
div_image(Img_1, Img_add0, Highpass, 1, 0) // 1 / (1 + (D0/D)^(2*n1))
set_grayval(Highpass, 0.5*Img_Height, 0.5*Img_Width, 0)
else
return()
endif
* stop()
convol_fft(Img_fft0, Highpass, fft_highpass)
fft_generic(fft_highpass, log_filt0, 'from_freq', 1, 'sqrt', 'dc_center', 'real')
exp_image(log_filt0, Img_filt0, 'e')
scale_image_max(Img_filt0, Img_max0)
convert_image_type(Img_max0, Img_filt, 'byte')
stop()
return ()5.运算结果
5.1原图
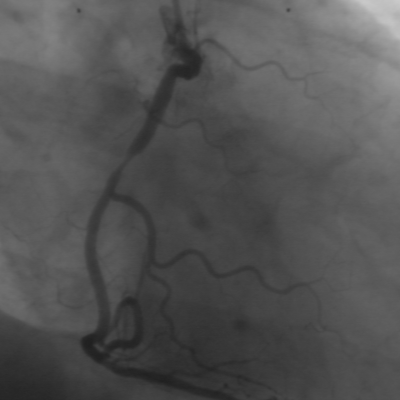
5.2结果图片
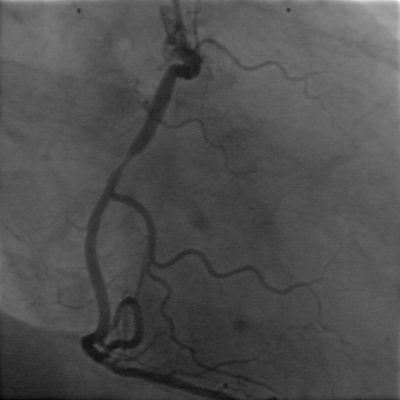
6.总结
本质上,同态滤波器是一种抑制低频增强高频的频域滤波器。任何符合这种特点的滤波器形式,都可以视为同态滤波器。本文封装了3种不同形式的同态滤波器算子。
高斯高通滤波器,可通过修改其参数,观察不同的处理结果。
改进的高斯高通滤波器,可修改其、
、c、
参数,观察不同的处理结果。
巴特沃斯滤波器,可修改其阶数n、参数,观察不同的处理结果。
参考资料:






















 1041
1041

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








