本文解析了四道算法竞赛题目，包括海港统计、回文日期查找、求和问题及推销员路径规划，涵盖数据结构、模拟算法、数学推导及贪心策略。
A 海港
输出
输出n行，第i行输出一个整数表示第i艘船到达后的统计信息。
样例输入
3
1 4 4 1 2 2
2 2 2 3
10 1 3
样例输出
3
4
4
提示
【样例解释1】
第一艘船在第1秒到达海港，最近24小时到达的船是第一艘船，共有4个乘客， 分别是来自国家4,1,2,2共来自3个不同的国家；
第二艘船在第2秒到达海港，最近24小时到达的船是第一艘船和第二艘船，共有4 + 2 =6个乘客，分别是来自国家4,1,2,2,2,3共来自4个不同的国家；
第三艘船在第10秒到达海港，最近24小时到达的船是第一艘船、第二艘船和第 三艘船，共有4+ 2+1=7个乘客，分别是来自国家4,1,2,3共来自4个不同 的国家。
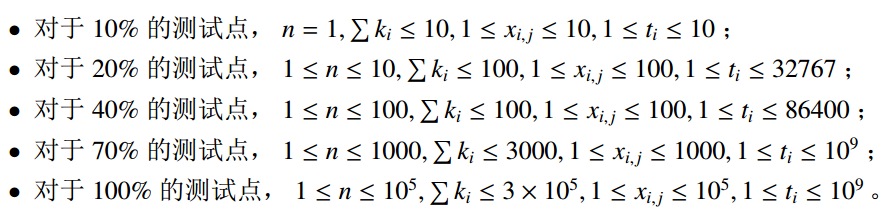
因为这个题只记录在一艘船到达的时间前24小时内的人的国籍，这样有来的也有走的，先到的先走，所以是不是想到了一个数据结构呢？没错，用队列来模拟就好了，但是如果每一秒每一秒的来存，那么需要10^9的数组，很显然是不行的，这时候看到人的总和只有3×10^5，那么就按人来存好了，这样只需要3×10^5的数组，还要注意在24小时前的船只也要走，也就是不包括正好24小时前的。
#include<bits/stdc++.h>
#define exp 1e-8
#define mian main
#define pii pair<int,int>
#define pll pair<ll,ll>
#define ll long long
#define pb push_back
#define PI acos(-1.0)
#define inf 0x3f3f3f3f
#define w(x) while(x--)
#define int_max 2147483647
#define lowbit(x) (x)&(-x)
#define gcd(a,b) __gcd(a,b)
#define pq(x) priority_queue<x>
#define ull unsigned long long
#define scn(x) scanf("%d",&x)
#define scl(x) scanf("%lld",&x)
#define pl(a,n) next_permutation(a,a+n)
#define ios ios::sync_with_stdio(false)
#define met(a,x) memset((a),(x),sizeof((a)))
using namespace std;
const int N=3e5+10;
int n;
struct node
{
int time;
int p;
};
int gj[N];
queue<node>q;
int main()
{
while(~scanf("%d",&n)){
int ans=0;
met(gj,0);
int t,c;
node m;
for(int i=1;i<=n;i++){
scanf("%d%d",&t,&c);
for(int j=1;j<=c;j++){
m.time=t;
scanf("%d",&m.p);
if(!gj[m.p])
ans++;
gj[m.p]++;
q.push(m);
}
while(1){
node mm=q.front();
if(mm.time+86400>m.time)
break;
gj[mm.p]--;
if(gj[mm.p]==0)
ans--;
q.pop();
}
printf("%d\n",ans);
}
}
}
D 回文日期
题目描述
在日常生活中，通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用8位数字表示一个日期，其中，前4位代表年份，接下来2位代表月 份，最后2位代表日期。显然：一个日期只有一种表示方法，而两个不同的日期的表 示方法不会相同。
牛牛认为，一个日期是回文的，当且仅当表示这个日期的8位数字是回文的。现 在，牛牛想知道：在他指定的两个日期之间包含这两个日期本身），有多少个真实存 在的日期是回文的。
一个8位数字是回文的，当且仅当对于所有的i(1<= i <= 8)从左向右数的第i个 数字和第9-i个数字（即从右向左数的第i个数字）是相同的。
例如：
•对于2016年11月19日，用8位数字20161119表示，它不是回文的。
•对于2010年1月2日，用8位数字20100102表示，它是回文的。
•对于2010年10月2日，用8位数字20101002表示，它不是回文的。
每一年中都有1212个月份：
其中，1,3,5,7,8,10,121,3,5,7,8,10,12月每个月有31天；4,6,9,114,6,9,11月每个月有30天；而对于22月，闰年时有29天，平年时有28天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种：
1.这个年份是4的整数倍，但不是100的整数倍；
2.这个年份是400的整数倍。
例如：
•以下几个年份都是闰年：2000,2012,20162000,2012,2016。
•以下几个年份是平年：1900,2011,20141900,2011,2014。
输入
两行，每行包括一个8位数字。
第一行表示牛牛指定的起始日期。
第二行表示牛牛指定的终止日期。
保证date_i和都是真实存在的日期，且年份部分一定为4位数字，且首位数字不为0。
保证date 1 —定不晚于date 2。
输出
一个整数，表示在date1和date2之间，有多少个日期是回文的。
样例输入
20110101
20111231
样例输出
1
提示
样例说明】
对于样例1，符合条件的日期是20111102。
对于样例2，符合条件的日期是20011002和20100102。
【子任务】
对于%60的数据，满足date1 = date2
这个题目直接模拟就好了，可能有一些麻烦，首先需要一个函数判断一下当前年份是否为闰年，还需要判断是否到达终止日期，
另外在就是判断回文了，并且我们可以看出每一年只可能有一个回文日期，所以当有一年有回文日期后，直接进入下一年即可
#include<bits/stdc++.h>
#define exp 1e-8
#define mian main
#define pii pair<int,int>
#define pll pair<ll,ll>
#define ll long long
#define pb push_back
#define PI acos(-1.0)
#define inf 0x3f3f3f3f
#define w(x) while(x--)
#define int_max 2147483647
#define lowbit(x) (x)&(-x)
#define gcd(a,b) __gcd(a,b)
#define pq(x) priority_queue<x>
#define ull unsigned long long
#define sc(x) scanf("%d",&x)
#define scl(x) scanf("%lld",&x)
#define pl(a,n) next_permutation(a,a+n)
#define ios ios::sync_with_stdio(false)
#define met(a,x) memset((a),(x),sizeof((a)))
using namespace std;
int x,y,yy,y2,m1,m2,d1,d2;
int day[13]={0,31,28,31,30,31,30,31,31,30,31,30,31}; //这里二月的天数写28,29都行，到时需要特判
int rn(int x)
{
return ((x%4==0&&x%100!=0)||x%400==0)?29:28;
}
bool check()
{
return (yy<y2||(yy==y2&&m1<m2)||(yy==y2&&m1==m2&&d1<=d2));
}
bool cz(int y,int m,int d)
{
int s[8];
int p=y*10000+m*100+d;
for(int i=0;i<8;i++){
s[i]=p%10;
p/=10;
}
for(int i=0;i<4;i++)
if(s[i]!=s[7-i])
return false;
return true;
}
int main()
{
while(~scanf("%d%d",&x,&y)){
int ans=0;
yy=x/10000;y2=y/10000; //年
m1=(x/100)%100;m2=(y/100)%100; //月
d1=x%100;d2=y%100; //日
while(check()){
bool falg=true;
if(cz(yy,m1,d1)){
ans++;
yy++;
m1=1;
d1=1;
continue;
}
if((m1==2&&d1==rn(yy))||m1!=2&&d1==day[m1]){
m1++;
d1=1;
falg=false;
}
if(m1==13){
yy++;
m1=1;
d1=1;
falg=false;
}
if(falg)
d1++;
}
printf("%d\n",ans);
}
}
E 求和
一条狭长的纸带被均匀划分出了n个格子，格子编号从1到n。每个格子上都染了一种颜色color_i用[1,m]当中的一个整数表示，并且写了一个数字number_i。
定义一种特殊的三元组:(x,y,z)，其中x,y,z 都代表纸带上格子的编号，这里的三元组要求满足以下两个条件：
- xyz是整数,x<y<z,y-x=z-y
- colorx=colorz
满足上述条件的三元组的分数规定为(x+z) *(number_x+number_z)。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大，你只要输出整个纸带的分数除以10,007所得的余数即可。
输入
第一行是用一个空格隔开的两个正整数n和m,n表纸带上格子的个数，m表纸带上颜色的种类数。 第二行有n用空格隔开的正整数，第i数字number表纸带上编号为i格子上面写的数字。 第三行有n用空格隔开的正整数，第i数字color表纸带上编号为ii格子染的颜色。
输出
共一行，一个整数，表示所求的纸带分数除以 10,007 所得的余数。
样例输入
6 2
5 5 3 2 2 2
2 2 1 1 2 1
样例输出
82
提示
【输入输出样例 说明】
纸带如题目描述中的图所示。
所有满足条件的三元组为：(1,3,5),(4,5,6)。
所以纸带的分数为(1+5)∗(5+2)+(4+6)∗(2+2) = 42+40 = 82。
【数据说明】
对于第 1 组至第 2 组数据， 1 ≤ n ≤ 100, 1 ≤ m ≤ 5,
对于第3 组至第 4 组数据， 1 ≤ n ≤ 3000, 1 ≤ m ≤ 100
对于第 5 组至第6组数据， 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000且不存在出现次数超过20的颜色；
对 于 全 部 10 组 数 据 ， 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000,1≤color_i≤m,1≤number_i≤100000
首先看这个三元组， 分数的计算为(x+z) *(number_x+number_z)。
第一个条件x<y<z,y-x=z-y，我们可以看出x+z=2y。由此得出x，z同奇偶，因为一个偶数一个奇数是得不到一个偶数的。
然后看第二个条件，x,z的颜色要一样，那么我们可以把这一条纸带根据颜色和奇偶性分为2*m组，颜色相同且下标的奇偶性相同的就在一组。
接下来，我们只看其中一组的分数的求法，在这里 xi：代表这一组中第i个数的下标，yi：代表这一组第i个数代表的值是多少。
那么这一组的分数：
（x1+x2）*（y1+y2）+（x1+x3）*( y1+y3 )+......+（x1+xn）*（y1+yn）+
（x2+y3）*（y2+y3）+（x2+x4）*（y2+y4）+......+（x2+xn）*（y2+yn）+
......+
（xn-1+xn）*（yn-1+yn）。
,根据分配率展开，上面的第一行=(n-1)x1*y1+x1*（y2+y3+......+yn）+y1*（x2+x3+......+xn）+x2*y2+x3*y3+......+xn*yn,
然后下面的每一行，
行i=（n-i）*xiyi+xi*（y(i+1)+...yn）+yi*（(xi+1)+......+xn）+x（i+1）*y（i+1）+......+xn*yn
还是先看第一行的，我们如果拿出一个x1*y1放入x1*（y2+y3+......+yn）中，就成了x1*（y1+y2+y3+......+yn）,
再看y1*（x2+x3+......+xn），我们可以把这些依次放入下面的几行中，这样下面的行中xi×一系列y的就可以依次补全，
再把最后的x2*y2+x3*y3+......+xn*yn,也依次放入下面几行，
最后可以得出一个通项，对于每一个数i=(n-2)xi*yi+xi*(y1+y2+......+yn)。
over~
建议这个数学公式推导还是根据分奇偶的思路自己推一下，可能讲的不怎清晰。
#include<bits/stdc++.h>
#define exp 1e-8
#define mian main
#define pii pair<int,int>
#define pll pair<ll,ll>
#define ll long long
#define pb push_back
#define PI acos(-1.0)
#define inf 0x3f3f3f3f
#define w(x) while(x--)
#define int_max 2147483647
#define lowbit(x) (x)&(-x)
#define gcd(a,b) __gcd(a,b)
#define pq(x) priority_queue<x>
#define ull unsigned long long
#define sc(x) scanf("%d",&x)
#define scl(x) scanf("%lld",&x)
#define pl(a,n) next_permutation(a,a+n)
#define ios ios::sync_with_stdio(false)
#define met(a,x) memset((a),(x),sizeof((a)))
#define mod 10007
using namespace std;
const int N=1e5+10;
ll s[N][2],sum[N][2],a[N],color[N],n,m;
void init()
{
met(s,0);
met(sum,0);
met(a,0);
met(color,0);
}
int main()
{
while(~scanf("%lld%lld",&n,&m)){
init();
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=1;i<=n;i++){
scanf("%lld",&color[i]);
s[color[i]][i%2]++; //每一组中的数的数量
sum[color[i]][i%2]+=a[i]; //每一组中数的和，即y1+y2+......+yn
}
ll ans=0;
for(int i=1;i<=n;i++){
ans=(ans+(s[color[i]][i%2]-2)*a[i]*i%mod+i*sum[color[i]][i%2]%mod)%mod;
}
printf("%lld\n",ans);
}
}
F 推销员
题目描述
阿明是一名推销员，他奉命到螺丝街推销他们公司的产品。螺丝街是一条死胡同，出口 与入口是同一个，街道的一侧是围墙，另一侧是住户。螺丝街一共有 N 家住户，第 i 家住户 到入口的距离为 Si 米。由于同一栋房子里可以有多家住户，所以可能有多家住户与入口的 距离相等。阿明会从入口进入，依次向螺丝街的 X 家住户推销产品，然后再原路走出去。 阿明每走 1 米就会积累 1 点疲劳值，向第 i 家住户推销产品会积累 Ai点疲劳值。阿明 是工作狂，他想知道，对于不同的 X，在不走多余的路的前提下，他最多可以积累多少点疲 劳值.
输入
第一行有一个正整数 N，表示螺丝街住户的数量。 接下来的一行有 N 个正整数，其中第 i 个整数 Si表示第 i 家住户到入口的距离。数据保 证 S1≤S2≤…≤Sn<1e8。 接下来的一行有 N 个正整数，其中第 i 个整数 Ai表示向第 i 户住户推销产品会积累的 疲劳值。数据保证 Ai<1e3。
输出
输出 N 行，每行一个正整数，第 i 行整数表示当 X=i 时，阿明最多积累的疲劳值。
样例输入
5
1 2 3 4 5
1 2 3 4 5
样例输出
15
19
22
24
25
提示
【输入输出样例 说明】
X=1: 向住户 5 推销，往返走路的疲劳值为 5+5，推销的疲劳值为 5，总疲劳值为 15。
X=2: 向住户 4、5 推销，往返走路的疲劳值为 5+5，推销的疲劳值为 4+5，总疲劳 值为 5+5+4+5=19。
X=3: 向住户 3、4、5 推销，往返走路的疲劳值为 5+5，推销的疲劳值 3+4+5，总疲 劳值为 5+5+3+4+5=22。
X=4: 向住户 2、3、4、5 推销，往返走路的疲劳值为 5+5，推销的疲劳值 2+3+4+5， 总疲劳值 5+5+2+3+4+5=24。
X=5: 向住户 1、 2、 3、 4、 5 推销，往返走路的疲劳值为 5+5，推销的疲劳值 1+2+3+4+5， 总疲劳值 5+5+1+2+3+4+5=25。
一道贪心的题目，每一次都是在上一次的情况下进行更新，一开始的思路是先找到从起点开始到那n个点中总疲劳值最大的，在分别看往左走和往右走哪个疲劳度消耗的更多，注意在这种情况下：
向左走只需要加上推销的疲劳值，因为他已经走过这里了，就等于顺路推销
向右走的话需要 当前点的距离减去他之前的点的距离×2+推销当前的花费，也就是(a[i].dis-a[now].dis)*2+a[i].w。在更新一下now，就是那个当前最远到达的点。
当向左走和向右走花费一样的时候，无所谓哪个了，都可以的。
把向左走和向右走的比较一下就好了，但是不知道什么原因在洛谷只过了30......orz
然后想到向左走的的用大根堆优化一下（优先队列），，只需要计算向右走的就好了。
具体看代码。。。
#include<bits/stdc++.h>
#define exp 1e-8
#define mian main
#define pii pair<int,int>
#define pll pair<ll,ll>
#define ll long long
#define pb push_back
#define PI acos(-1.0)
#define inf 0x3f3f3f3f
#define w(x) while(x--)
#define int_max 2147483647
#define lowbit(x) (x)&(-x)
#define gcd(a,b) __gcd(a,b)
#define pq(x) priority_queue<x>
#define ull unsigned long long
#define sc(x) scanf("%d",&x)
#define scl(x) scanf("%lld",&x)
#define pl(a,n) next_permutation(a,a+n)
#define ios ios::sync_with_stdio(false)
#define met(a,x) memset((a),(x),sizeof((a)))
using namespace std;
const int N=1e5+10;
int n;
priority_queue<int>q;
struct node
{
int dis;
int w;
}a[N];
int main()
{
while(~scanf("%d",&n)){
for(int i=1;i<=n;i++)
sc(a[i].dis);
for(int i=1;i<=n;i++)
sc(a[i].w);
int now=0;
q.push(0);
int ans=0;
for(int i=1;i<=n;i++){
int p=q.top();
int pp=now;
int maxn=0;
for(int i=now+1;i<=n;i++)
if((a[i].dis-a[now].dis)*2+a[i].w>maxn){
pp=i;
maxn=(a[i].dis-a[now].dis)*2+a[i].w;
}
if(maxn>p){ //比较是否向右走比向左走花费高
q.push(maxn); //高就讲右边的入队
for(int i=now+1;i<pp;i++)
q.push(a[i].w);
now=pp;
}
ans+=q.top(); //更新答案
q.pop();
printf("%d\n",ans);
}
}
}
/*
5
1 2 2 4 5
5 4 3 4 1
*/
扫一扫
2362
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
