宽带变压器匹配网络设计

A宽带变压器型匹配网络的分析与设计 网络

Chen Xing1, 金桂祥1, 李通1, 颜娜1*, 陈勇2,3, 林越2,3, 徐宏涛1
1专用集成电路与系统国家重点实验室，复旦大学，上海 201210，中国
2艾科莱特微电子有限公司，上海 201203，中国
3艾科莱特微智能（苏州）有限公司，苏州 215000，中国
* 邮箱：yanna@fudan.edu.cn

摘要

本文提出了一种针对宽带变压器型匹配网络的具体分析与设计策略。该结构由一个变压器和在两个端口处的两个并联电容器组成。给出了一个设计实例，仿真结果表明，在27G至33G频带内，插入损耗小于1.5dB，纹波小于0.15dB。

1. 引言

宽带收发器日益增长的需求促使人们寻找宽带技术。
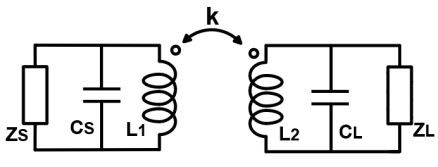
如图1所示，基于变压器的匹配网络由于其优势，是用于宽带匹配的最常用结构之一。首先，变压器仅占据单个片上电感[1]的空间。其次，并联电容器可以吸收有源部分引入的电容。第三，变压器可以在级间提供完美的直流隔离。图2显示了该匹配网络的等效电路，可将其视为一个四阶匹配网络。该结构可在两个频率点[1][2]实现完美的阻抗匹配。如果带内纹波被最小化，则可实现宽带匹配网络。实际上，由于品质因数较低，片上电感会引入较大的损耗。有源电路的最佳阻抗在宽带范围内会发生变化。这些非理想特性会导致带宽恶化和插入损耗增加，因而需要新的基于变压器的匹配网络设计方法。
本文提出了基于变压器的匹配网络的分析和一种系统化设计策略。给出了一个设计实例以验证精度，并提供了在台积电40纳米CMOS工艺下的仿真结果。

2. 基于变压器的匹配网络设计分析

2.1 理想情况

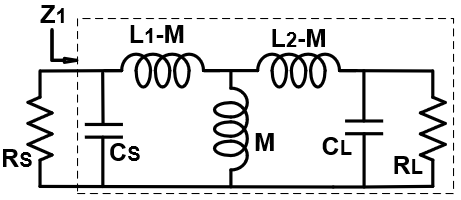
在理想情况下，我们假设图2所示的电感和电容是无损耗的。负载和源阻抗都被转换为恒定电阻与并联电容器的形式。此处的电容器分别由CS 和CL 表示。
根据匹配要求，如公式(1)所示，可以推导出公式(2)(3)，其中，

$$
\frac{1}{\omega_1} = \sqrt{\frac{1}{L_1 C_S}}, \quad \frac{1}{\omega_2} = \sqrt{\frac{1}{L_2 C_L}},
$$
$$
Q_S = \frac{1}{\omega_1 C_S R_S}, \quad Q_L = \frac{1}{\omega_2 C_L R_L}.
$$

$$
Z_S = R_S \tag{1}
$$
$$
\omega^4 - \left(1 - k^2\right)\left(Q_S^2 + Q_L^2\right)\omega^2 + \left(1 - k^2\right)^2 Q_S^2 Q_L^2 = 0 \tag{2}
$$
$$
\frac{s L_1}{R_S} - \frac{s L_2}{R_L} - \frac{k^2 s^2 L_1 L_2}{R_S R_L} = -\left(1 - k^2\right) \tag{3}
$$

$$
\omega_1 = \omega_2, \quad Q_S = Q_L \tag{4}
$$

这表明，只要满足公式(4)，该网络在两个不同的频率点上就能实现匹配。

2.2 有损变压器

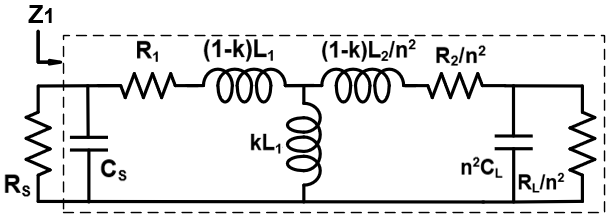
由于片上电感在匹配网络中引入的损耗远大于电容器，因此在分析中我们重点关注变压器引入的损耗。初级和次级电感的等效串联寄生电阻R1, R2由公式(5)给出，其中q1、q2分别为初级和次级电感的品质因数。
图3显示了该情况下的等效电路。为了最小化插入损耗，匹配网络[4]的效率在公式(6)中给出。这表明当次级电感和负载电容满足公式(7)(8)时，在特定频率 ω0下将实现最大效率，此时负载阻抗的最优Q值被确定，其中。

$$
Q_L = \omega L / R
$$
$$
q_1 = \omega L_1 / R_1, \quad q_2 = \omega L_2 / R_2 \tag{5}
$$

$$
\eta = \frac{R_e}{R_e + R_q + (\omega L_q)^2 / (R_e + R_q)} \tag{6}
$$

$$
\omega_0^2 = \frac{1}{L_2 C_L}, \quad A = 1 + \frac{1}{q_2^2} + \frac{k^2}{q_1^2} + \frac{1}{q_2^2} \tag{7}
$$
$$
Q_{L,opt} = \frac{1}{\omega C_L R_L} = \sqrt{1 + \frac{1}{q_2^2}} \tag{8}
$$

然而，该最优负载电容并不总是可行。当负载阻抗的 Q值超过该最优值时，其效率会下降，且效率不仅与 k、q1、q2有关，还与负载阻抗相关。在这种情况下，最优电感遵循公式(9)，并且不会添加额外电容器，因为此时我们希望获得较低Q值。

$$
\frac{1}{q_{eq}^2} = \frac{R_2}{\omega L_2} + k^2 \frac{R_1}{\omega L_1} + \frac{1}{q_2^2} + \omega^2 C_L^2 R_2^2 \tag{9}
$$

为了确保在频带内阻抗变换足够精确，根据图3，阻抗匹配条件应为。分别计算实部和虚部，可推导出公式(11)(12)。

$$
Z_S = R_S
$$

$$
\omega^4 - (1 - k^2)(Q_S^2 + Q_L^2)\omega^2 + (1 - k^2)^2 Q_S^2 Q_L^2 - \frac{Q_S q_1 + Q_L q_2}{\omega^2} = 0 \tag{11}
$$

$$
\left[\frac{\omega^2 L_1 C_S}{R_S} - \frac{\omega^2 L_2 C_L}{R_L}\right]\left(1 - k^2\right) + \frac{k^2 \omega^2 L_1 L_2}{R_S R_L} = \left(R_S - R_L\right) + \left(\omega C_S R_S^2 - \omega C_L R_L^2\right) \tag{12}
$$

与公式(3)相比，公式(12)明显显示出两个频率之间存在一些失配。考虑频带内的阻抗变化。幸运的是，在许多情况下，阻抗变化通常遵循一定的规律，因为大部分虚部是由并联或串联连接的寄生电容引入的。
总之，设计匹配网络时，负载阻抗ZL、目标阻抗ZS 和频率范围(ωL ~ω H)是已知量，初级/次级电感品质因数q1/q2受限，且对阻抗变换影响较小，因此也可以在初期进行估计。
首先，将负载阻抗转换为一个电阻和一个电容并联连接的形式。考虑平坦度的电路，效率应在频带的中心频率处最大化。根据之前提到的负载阻抗的Q值，提出了两种不同的策略来选择L2, CL。这里，我们假设 QS=QL用于估算，因此，已知ωL、 ωH和公式(11)，即可计算k和ω1 。L1可由公式(9)推导得出，CS的值相应确定。为了消除由公式(12)和非恒定阻抗引起的失配，分别在1处计算LωL和 ωH的值，并选取平均值。与其它工作中采用的迭代计算相比，该设计策略直接计算匹配网络的参数，具有足够的精度。

3. 设计示例与仿真结果

例如，负载阻抗为50 Ω，目标匹配阻抗是在27~33 GHz范围内变化的变量，具体如表1所示。匹配网络的参数使用MATLAB语言计算得出，如表2所示。

表1. 目标匹配阻抗

频率	27G	30G	33G
阻抗	41-j104 Ω	36-j92 Ω	35-j87 Ω

表2. 设计的匹配网络参数

k	Lpri	Lsec	CS	CL
0.42	546 皮亨	122 皮亨	10 fF	304 fF

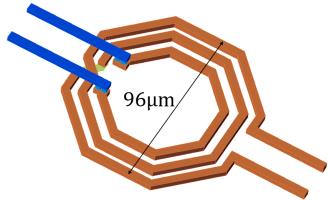
使用台积电40纳米CMOS工艺的匹配网络的仿真和计算的插入损耗及输入阻抗如图5所示。

4. 总结

本文描述了一种基于变压器的宽带匹配网络的系统化设计策略。该设计考虑了频带内的阻抗变化以及变压器引入的损耗，以实现具有最小化插入损耗的宽带匹配。文中给出了一个示例并展示了其仿真结果。使用MATLAB语言编写的计算程序仅需15ms即可完成所有参数的计算。在27GHz~33GHz范围内，实现了插入损耗<1.5dB和带内波动<0.15dB的性能。