MapReduce推测执行策略综述

原创于 2025-10-25 11:19:50 发布 · 749 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#推测执行 #MapReduce #异构环境 #MCP #ex-MCP

MapReduce中推测执行策略的综述

1 引言

随着互联网技术的创新，不仅网络传输速率不断提升，而且互联网用户数量也呈爆炸式增长，这充分表明大数据时代正在到来[1]。前雅虎!工程师道格·卡廷将其搜索引擎项目与谷歌发表的三篇论文[2–4]相结合，实现了一个名为“Hadoop”的分布式并行计算系统[5],，并由阿帕奇软件基金会完全开源。

Hadoop 是一个用于存储和处理大规模数据集的开源框架，它使用名为 HDFS 的分布式文件系统将数据块存储在 DataNode 中，从而实现高容错性，并使用 MapReduce 进行处理。

这些数据在许多廉价节点上并行处理。随着Hadoop平台的不断发展和完善，基于HDFS和MapReduce的上层应用变得越来越丰富，例如称为HBase、Hive和Pig[6–10]的分布式数据库。

MapReduce是一种专用于海量数据计算的并行处理模式，它将计算过程分为 Map和Reduce两个阶段。Map阶段基于数据集对对进行处理，并输出中间的；随后Reduce阶段合并所有具有相同中间键值的中间值 [3]。MapReduce框架由三部分组成：客户端、JobTracker和TaskTracker。客户端用于提交作业；JobTracker负责将作业分解为Map和归约任务，并将其分配给各个TaskTracker；TaskTracker则并行执行这些任务[11]。

任务调度器是MapReduce中任务分配的核心组件，旨在通过获取 TaskTracker的运行状态来调度所有任务按适当顺序执行，并缩短执行时间。

然而，JobTracker无法访问所有实时执行信息，也难以预测任务未来的运行状态。因此，它只能在任务分配时让作业以最快的方式执行，但不能保证该分配方式在后续执行过程中仍保持优势[12]。为了改善由于节点或任务调度器中意外问题导致的性能下降，并减少这些问题带来的损失，MapReduce引入了推测执行，即在备用节点上备份慢任务，期望以此减少整个作业的执行时间。谷歌应用了朴素策略的推测执行，观察到推测执行可将作业执行时间减少44%[3]。

除了Hadoop之外，推测执行也在Microsoft Dryad中得以实现[13]。

鉴于推测执行在MapReduce中的重要性，本文综述了近年来为提升 MapReduce性能而开展的关于推测执行的研究，包括其相对的优缺点。本文结构如下：第2节介绍了推测执行的概述。第3节介绍了在异构环境中为优化推测执行而设计的多种策略。第4节分析了这些方法的优点和局限性。最后，第 5节对全文进行总结。

2 推测执行概述

2.1 推测执行

由于软件缺陷、负载不均衡或资源分布不均等原因，会导致同一作业中多个任务的运行速度不一致，某些任务的运行速度明显慢于其他任务（例如，某个任务的进度仅为10%，而所有其他任务均已运行完毕），这些任务会拖慢整个作业的执行进度，被称为“拖后任务”。为了防止这种情况发生，MapReduce采用推测执行机制[3]；MapReduce将启动一个备份任务，并让该备份任务与原始任务同时运行；然后 MapReduce以最先完成的任务输出结果作为最终结果。

任务的结果。可以看出，这种机制体现了“以空间换时间”的思想。从描述中可以发现推测执行的三个关键点：

找出“拖后任务”，这要求MapReduce系统以高效的方式识别出拖后任务。如果将正常任务误判为落后任务，并在另一个节点上启动备份任务执行，将会增加执行时间并消耗集群资源。
在更快的节点上启动备份任务。MapReduce系统需要一种有效的机制来衡量节点处理任务的能力，以找到更快的节点来启动备份任务。
确保备份任务的执行对集群带来有效性。备份任务的执行应能够减少作业执行时间并提高集群吞吐量。

2.2 Hadoop 朴素策略

为了选择慢任务，Hadoop 实现了最原始的推测执行，称为 Hadoop‐NAÏVE [14]。在此策略中，MapReduce 根据返回的心跳包信息计算当前阶段每个任务的进度，记为 Pst，可通过公式（1）计算：

$$
Pst = \frac{Y}{N} \quad (1)
$$

其中，Y 是此阶段已处理的键值对数量，N 是此阶段需要处理的键值对总数。

MapReduce 包含映射任务和归约任务。例如，如果 t 是一个映射任务，则其进度可通过（1）计算。然而，如果 t 是一个归约任务，并且已经完成 finishedfirstM(M2（0,1,2））阶段的归约任务，该任务包含 shuffle、排序和归约三个阶段，每个阶段占进度的三分之一，则其进度需要单独计算。任务t的进度，记为Pt ，可通过公式（2）计算。因此，作业中所有任务的平均进度，记为Pavg，可通过公式（3）计算。

$$
Pt =
\begin{cases}
Pst & \text{t is map task} \
\frac{1}{3} \times M + \frac{1}{3} \times Pst & \text{t is a reduce task}
\end{cases}
\quad (2)
$$

$$
Pavg = \frac{\sum_{i=1}^{K} Pt[i]}{K} \quad (3)
$$

其中K是任务数量，Pt[i]是任务i的进度。

Naïve finds the Straggler by comparing the progress of the task with the average progress of all the tasks. When the task runs more than 60秒 and meets the following requirements (4), then it a 落后任务:

$$
Pavg - Pt \geq 20\% \quad (4)
$$

由于Naïve假设整个集群是同构的，因此需要通过公式(find the “拖后任务”由公式(4)来识别，但该策略在异构集群环境中存在诸多缺陷。因此，有必要改进Hadoop的推测执行策略以适应异构环境。

3 异构环境中的推测执行优化

为了提高推测执行在异构环境中的性能，许多研究人员讨论了推测执行的缺陷，并提出了一系列改进方案。在本节中，总结了几种改进的推测执行策略。

3.1 最长近似结束时间算法

Zaharia等人提出了最长近似结束时间（LATE）算法，以提高在异构环境中的性能 [15]。LATE的核心思想是选择剩余时间最长的任务作为“落后任务”并在快速节点上重新执行。任务 tk的进度速率，记为 PRk，用于通过公式(5)计算任务 tk的剩余时间，因此剩余时间（标记为RTk）可通过公式(6)进行评估，其中 T为执行时间。

$$
PRk = \frac{Pk}{T} \quad (5)
$$

$$
RTk = \frac{1 - Pk}{PRk} \quad (6)
$$

3.2 最大成本性能策略

陈等人提出了最大成本性能（MCP）策略 [16],，该策略通过确保推测执行能为集群带来更高的收益，来判断是否值得启动备份任务。

在MCP中，使用指数加权移动平均（EWMA）速率来预测任务未来的进度速率，而不是使用平均速率。EWMA速率可通过（7）计算，其中E(t)和 Y(t)分别表示在t时刻评估的和观测到的进度速率，λ reflects历史测量值的权重，并根据实验设置为0.2。

$$
E(t) = \kappa \cdot Y(t) + (1 - \kappa) \cdot E(t - 1) \quad 0 < \kappa < 1 \quad (7)
$$

与LATE不同，MCP中的剩余时间（RT）是当前阶段的剩余时间（RTcp）和后续阶段的剩余时间（RTfp）之和，如公式（8）和（9）所示。其中，est_timep通过后续阶段的平均进度速率进行估算，而f actord表示任务输入大小与所有任务的平均输入大小之比。

$$
RT = RTcp + RTfp = \frac{rem_datacp}{bandwidthcp} + \sum_{p \in fp} est_timep \cdot factord \quad (8)
$$

$$
factord = \frac{datainput}{dataavg} \quad (9)
$$

此外，备份任务的执行时间，标记为Tbackup，可以通过est_timep使用(10)来估计。

$$
Tbackup = \sum_{p} est_timep \cdot factord \quad (10)
$$

MCP 建立了一个成本效益模型以确保推测执行的效率，其中成本表示任务占用的槽位，收益表示节省的时间。启动一个备份任务将消耗两个槽位 Tbackup，并节省一个槽位 RT‐Tbackup；而不启动备份任务则会占用一个槽位达 RT 时间，且无任何节省。因此，这两种操作的收益可表示如下：

$$
profit_{backup} = \alpha \cdot (RT - Tbackup) - 2 \cdot \beta \cdot Tbackup \quad (11)
$$

$$
profit_{not_backup} = -\beta \cdot RT \quad (12)
$$

其中 α和 β分别是收益和成本的权重。如果任务满足(13)，则可被选为备用候选任务。

$$
profit_{backup} > profit_{not_backup}, \quad \frac{RT}{Tbackup} > \frac{\alpha + 2\beta}{\alpha + \beta} \quad (13)
$$

该公式可以通过使用 γ替换 β/α 进行简化，并变为（14）。γ被设为负载_因子，即Hadoop集群的负载因子，可通过（15）计算得出，其中 numberpendingtasks和 num_freeslots分别表示待处理任务的数量和空闲槽位的数量。

$$
\frac{RT}{Tbackup} > \frac{1 + 2\gamma}{1 + \gamma} \quad (14)
$$

$$
\gamma = load_factor = \frac{number_pending_tasks}{number_free_slots} \quad (15)
$$

通过遍历所有满足以下条件（17）的正在运行的任务，可以获得一组备份候选任务，然后将具有最长剩余时间（RT）的候选任务作为最终的备份任务finally。

$$
profit_{backup} > profit_{not_backup}, \quad \frac{RT}{Tbackup} > \frac{1 + 2 \cdot load_factor}{1 + load_factor} \quad (16)
$$

3.3 扩展最大成本性能（ex‐MCP）策略

黄等人改进了MCP策略并设计了扩展最大成本性能（ex‐MCP）策略 [17]。该策略的主要改进包括以下几个方面：

根据数据分布将映射任务划分为三类：数据本地、机架本地和非机架本地，从而更有效地分析任务执行信息，并更准确地判断“落后任务”
考虑任务所占用槽位的价值，旨在计算真实的集群资源成本
优先选择快速节点，然后使用ex‐MCP模型判断在该节点上是否值得对任务进行备份。而不是先使用 MCP模型选择慢任务，再寻找快速节点执行。前者更为准确和便捷

ex‐MCP的创新之处在于引入了每个槽位的价值，该价值可用任务执行时间的倒数（1/t）表示。类似于MCP，备份与不_备份的收益可建模如下：

$$
profit_{backup} = \alpha \cdot (RT - Tbackup) \cdot \frac{1}{Toriginal} - \beta \cdot \left( \frac{1}{Toriginal} + \frac{1}{Tbackup} \right) \quad (17)
$$

$$
profit_{not_backup} = -\beta \cdot RT \cdot \frac{1}{Toriginal} \quad (18)
$$

其中RT表示任务在原始节点上的剩余时间，可通过MCP中的公式(8)获得，Toriginal表示任务在原始节点上的执行时间，可通过各阶段的平均处理速率进行估算，Tbackup表示通过公式(10)计算出的任务在备份节点上的执行时间。α和 β分别为收益和成本的权重。

ex‐MCP得出如下结论，其中 γ是负载_因子，定义于公式(15)。是否启动推测执行由公式(19)决定。

$$
profit_{backup} \geq profit_{not_backup}, \quad RT \geq Tbackup + \frac{\gamma}{1 + \gamma} \cdot Toriginal \quad (19)
$$

3.4 使用线性关系模型估计剩余时间

在推测执行的早期研究中，研究人员未考虑系统负载对执行时间的影响。黄等人提出了基于线性关系模型估计剩余时间的方法（ERUL）[17, 18]。该策略利用系统负载与执行时间之间的近似线性关系来估计剩余执行时间，其公式如下：

$$
RTest = \frac{(1 + Zest) \cdot RTnow}{1 + Znow} \quad (20)
$$

其中RTest表示估计的剩余时间，当系统负载保持为Znow时，剩余时间记为RT now，而Zest是平均负载。

MCP模型也被用于保证推测执行的有效性，且慢任务候选者应满足公式 (21)，其中RT由ERUL计算得出，Tbackup基于以下表达式(22)计算，γ也是 Hadoop集群的负载_因子。

$$
\frac{RT}{Tbackup} > \frac{1 + 2\gamma}{1 + \gamma} \quad (21)
$$

$$
backup_time =
\begin{cases}
procCap \cdot Datatotal & \text{for map task} \
procCap & \text{for reduce task}
\end{cases}
\quad (22)
$$

其中 procCap表示被选中执行此类备份任务的节点的处理能力。当某个节点的 procCap高于所有节点的平均procCap时，该节点被判定为快速节点；反之则为慢速节点。procCap的计算分为两种情况：一种是该节点从未处理过此类任务，另一种是该节点已处理过相同类型的任务。procCap可用（23）表示，其中Tcost是该类型任务首次运行所花费的时间，first running task in this typeand the RT由ERUL计算得出。

$$
procCap =
\begin{cases}
\frac{Tcost + RT}{Datatotal} & \text{for map task} \
Tcost + RT & \text{for reduce task}
\end{cases}
\quad (23)
$$

相反，处理能力可以表述如下：

$$
procCap =
\begin{cases}
\eta \cdot preCap + (1 - \eta) \cdot \frac{exeTime}{Datatotal} & \text{for map task} \
\eta \cdot preCap + (1 - \eta) \cdot exeTime & \text{for reduce task}
\end{cases}
\quad (24)
$$

其中preCap是备份节点处理此类任务的先前处理能力，任务的执行时间标记为exeTime，η是平滑因子，设置为0.3。

总之，如果应用ERUL策略，整个过程如下：

根据非机架映射任务、非本地映射任务、本地映射任务和归约任务的顺序，优先选择“落后任务”候选。
估计该节点上的任务类型并确定该节点的处理能力
判断该节点是否为快速节点，如果不是，则返回第一步
使用MCP模型验证在此节点上启动备份任务的有效性，如果无效，则返回第一步
在此节点上启动一个备份任务。

4 几种优化策略的比较

4.1 各策略的优势与局限性

在MapReduce推测执行的研究中提出了几种策略，每种策略都有其优点和缺点，本节将逐一介绍。

通常，朴素策略将进度远落后于平均进度的任务视为低效任务，并在新节点上启动一个备份任务，它假设集群是同构的，因此在异构环境中无法获得良好的效果。

LATE 被设计为能够应对节点异构性和剩余时间最长的备份任务，这比仅根据任务进度进行判断更加公平，但也存在一些局限性：

LATE将归约阶段的三个子阶段的常数值设为1/3、1/3和1/3，但在实际执行环境中这些值会发生变化，导致进度计算不准确，并且由于剩余时间计算不准确而无法找到真正的慢任务。

MCP模型使用EWMA速率替代平均处理速率，并通过累加各阶段的剩余时间来计算总剩余时间，应用MCP模型可确保推测执行为集群带来收益，但仍然存在一些局限性：

MCP认为集群资源通过槽位来体现，并通过槽位的消耗反映备份任务开销，但不同节点性能不同，导致每个槽位的实际价值存在差异，因此在MCP中认为所有槽位具有相同价值是不合理的。
利用已知任务各阶段的平均执行时间以及因子d来估计备份_时间会产生一定误差。
在映射任务中，满足数据本地化的任务比不满足数据本地化的任务执行更快，因此将这些任务在同一层次上进行比较是不公平的。

ex‐MCP 旨在克服 MCP 的缺点。在成本‐性能模型的计算中考虑了槽位的取值，ex‐MCP 根据数据分布将映射任务划分为三类：数据本地、机架本地和非机架本地，进而分析任务执行信息并更准确地判断“落后任务”。

然而，备份时间的估算仍然采用MCP的方法，这将导致估算误差。

ERUL 发现了系统负载与执行时间之间的关系，并使用它们之间的线性关系来评估剩余时间，同时它还提供了一些改进措施以解决映射任务中的数据倾斜问题。然而，从实验结果来看，ERUL 更适合 CPU密集型任务，这可能是因为在计算密集型任务中，系统负载与执行时间之间的线性关系更为明显。

总之，所有这些策略在一定程度上都取得了良好的性能，各方法的主要优缺点列于表1中。此外，时间复杂度是评判算法优劣的一个非常重要的因素，如表2所示。MCP、ex‐MCP 和 ERUL 只需验证每个任务是否符合模型，因此它们的时间复杂度均为 O(n)，而 LATE 需要根据剩余时间对任务进行优先级排序，因此其时间复杂度为 O(nlogn)。

表1. 策略的优缺点

策略	优势	劣势
朴素策略	无特别优势	无法适应异构性
LATE	对异质性的鲁棒性	进度计算不准确
MCP	确保集群有效性	备份_时间的估计误差
ex‐MCP	考虑时隙的价值	备份_时间的估计误差
ERUL	线性关系更准确，适合CPU密集型	——

表2. 每种策略的时间复杂度

策略	LATE	MCP	ex‐MCP	ERUL
时间复杂度	O(nlogn)	O(n)	O(n)	O(n)

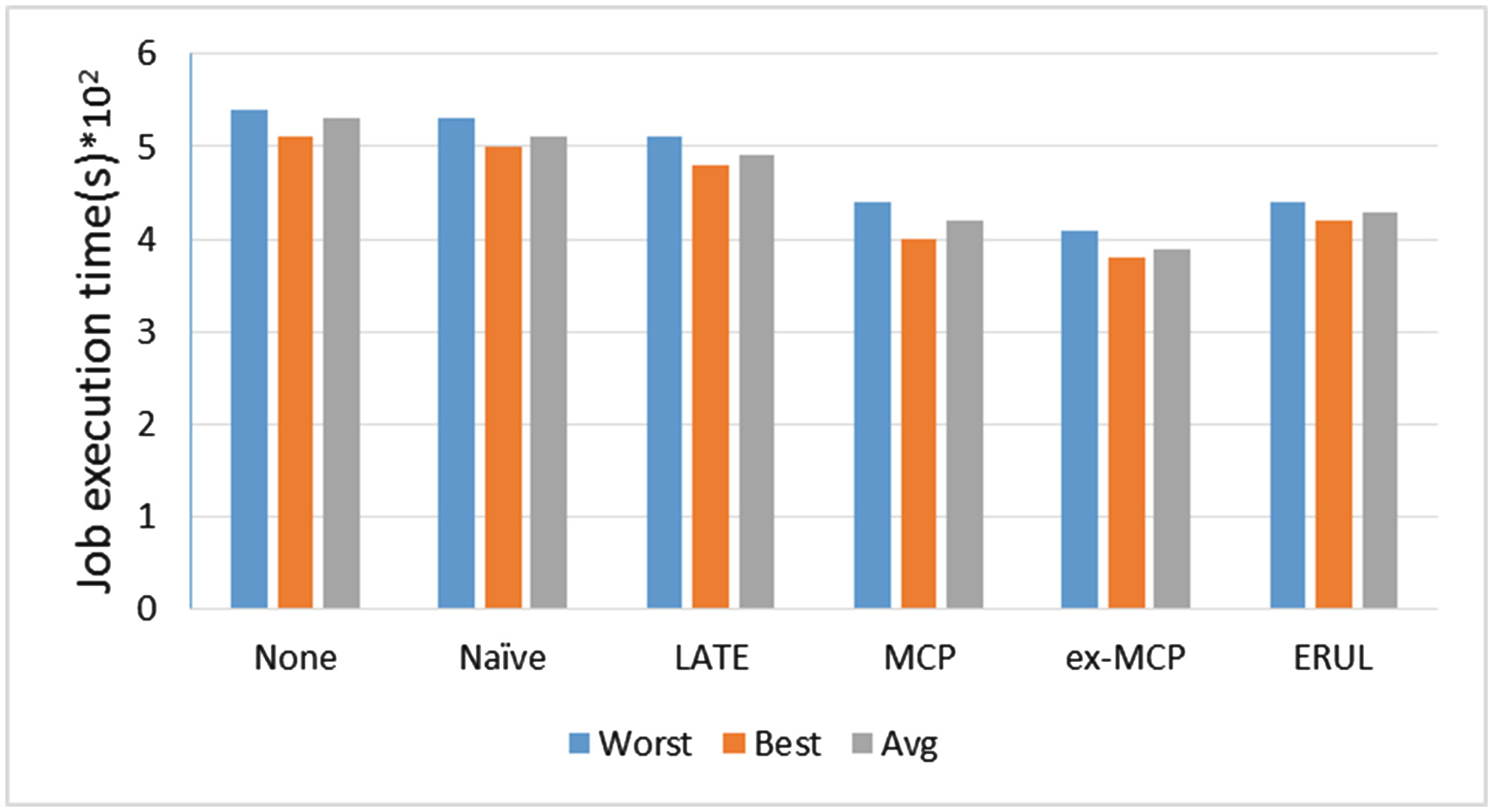
4.2 性能比较

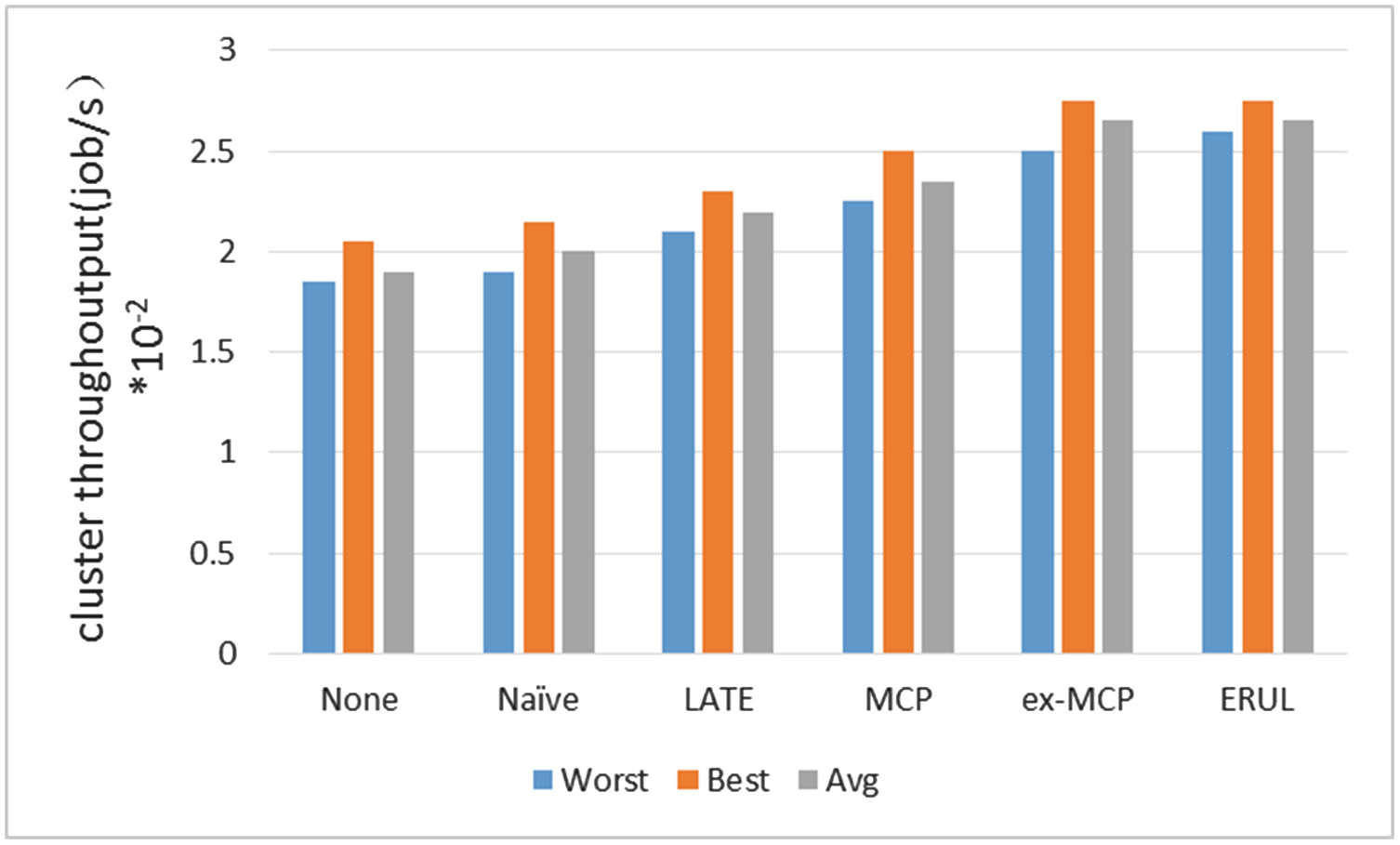
MapReduce 的性能指标通常定义为作业执行时间和集群吞吐量。作业执行时间是指一个作业中所有任务完成的时间，而集群吞吐量是指集群单位时间内能够处理的作业数量。图1显示了 WordCount 在最佳、最差和平均情况下的各种策略的执行时间。Gridmix2 常用于评估集群吞吐量，图2显示了每种策略在最佳、最差和平均情况下的集群吞吐量。从这两个图中可以看出，Hadoop‐无并未给集群带来太多好处，因此提出了若干策略以提升 MapReduce 相较于 Hadoop‐none 和 Hadoop‐无的性能。总体而言，我们可以看出 ex‐MCP 在执行时间和集群吞吐量方面均比其他策略更具优势。

然而，研究人员不仅与Hadoop‐朴素和Hadoop‐无进行比较，还与其他现有策略进行对比，以充分展示其优势。为了证明MCP的优越性，作者将其与LATE进行了比较，而LATE是此前提出的一种策略。在其之前的研究发现，MCP平均比LATE减少14%的作业执行时间，并将集群吞吐量提高9%。为优化MCP，研究人员提出了ex‐MCP，并对MCP与ex‐MCP进行了比较，实验结果证明，ex‐MCP比MCP减少了8%的作业执行时间，比LATE减少了21%的作业执行时间；在集群吞吐量方面，ex‐MCP比MCP提高了10%，比LATE提高了20%。ERUL的作业执行时间比LATE减少了12.5%，集群吞吐量比LATE提高了10%。

示意图0