【论文阅读笔记】Uncertainty quantification and attention-aware fusion guided multi-modal MR brain tumor segm

Zhou T, Zhu S. Uncertainty quantification and attention-aware fusion guided multi-modal MR brain tumor segmentation[J]. Computers in Biology and Medicine, 2023: 107142.

本文与“Feature fusion and latent feature learning guided brain tumor segmentation and missing modality recovery network”（解读）是同一作者，论文均是是杭州师范大学国家自然科学基金青年项目“深度学习指导下的缺失核磁共振模态图像的脑肿瘤分割与复发位置预测研究”支持研究，批准年份2022，项目编号：62206084。

一.论文核心思想概述

本文的核心思想是提出一种多模态MRI脑肿瘤分割方法，该方法结合了不确定性量化和注意力机制。通过应用基于贝叶斯模型的不确定性量化，将不确定性信息与输入的MR模态结合，然后将其用于深度学习网络以优化分割结果。此外，文中还介绍了一种注意力感知融合方法，用于融合多个MR模态的信息以提高分割性能。实验结果表明，不确定性量化可以提高分割准确性，并且这些组件可以轻松应用于其他网络结构和计算机视觉领域。

二.文章方法提出的背景

在本文的Introduction部分，提出了Uncertainty Quantification（不确定性量化）的背景：由于固有的不确定性，如MRI的低对比度或不同专家之间的注释的变化，医学分割问题往往是模糊的。不确定性量化的核心思想是量化模型对预测的不确定性，这在医学图像分割中尤为重要，因为不确定性信息可以帮助医生更好地理解模型的可信度。之前的应用方法通常包括了两种类型的不确定性量化：aleatoric uncertainty（随机不确定性）和epistemic uncertainty（认知不确定性）。

1. 随机不确定性（aleatoric uncertainty）：这种不确定性通常涉及到数据中的随机性和噪声。在脑肿瘤分割中，它可以用来描述图像中的噪声水平以及由于图像采集过程中的变化而导致的不确定性。随机不确定性的量化可以帮助模型更好地理解图像数据的不确定性来源。
2. 认知不确定性（epistemic uncertainty）：这种不确定性通常涉及到模型自身的不确定性，例如模型对未见数据的泛化能力。在脑肿瘤分割中，认知不确定性的量化可以用来估计模型对不同类型的肿瘤和不同图像特征的理解程度，这有助于识别模型在分割任务中可能出现错误的区域。

三.网络结构

网络整体结构为先使用3D Unet预分割，然后在分割的基础进行不确定性量化，产生Uncertainty Map,然后以此增加监督，进行第二阶段的精确分割。预分割不再赘述，就是常见的3D CNN。

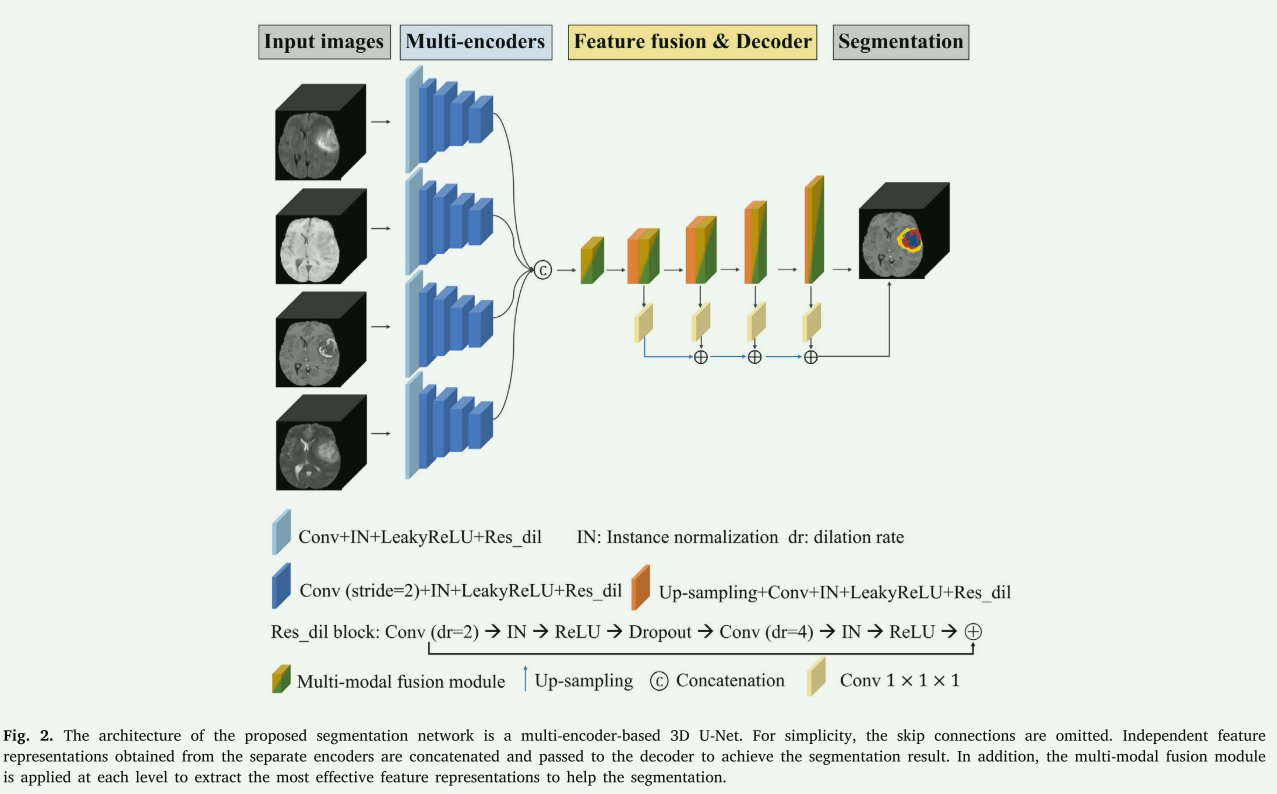
• Uncertainty quantification：这是本文主要创新点

  • 本文使用的是Monte Carlo (MC) Dropout，该方法是一种利用蒙特卡洛方法来估计神经网络不确定性的技术。在深度学习中，Dropout 是一种正则化技巧，它在训练过程中随机地将神经元的输出置零，以防止模型对训练数据过拟合。MC Dropout 利用了这一特性来估计模型的不确定性。MC Dropout 的基本思想是，在训练好的带有 Dropout 层的神经网络上，进行多次前向传播，每次都随机地启用或禁用 Dropout。通过多次前向传播得到的不同预测结果，可以用来估计输出的分布，从而获得关于预测的不确定性信息。

    具体步骤如下：

    1. 将训练好的神经网络模型应用到测试数据，启用 Dropout 层。
    2. 对测试数据进行多次前向传播，每次都以不同的 Dropout 配置进行。
    3. 收集每次前向传播的输出结果。
    4. 通过这些输出结果，计算均值和标准差，得到模型对每个预测的不确定性估计。

  • 本文中公式1是对采用的不确定量化的定义：这里展开说明一下

    $\begin{array}{c}{\mathrm{Var}}_{p(y\mid x,D)}\end{array}$