根据迭代,有:
| x' = y |
| y' = x - (a/b)*y |
int exgcd(int a, int b, int &x, int &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a%b, x, y);
int z = x;
x = y;
y = z - (a / b) * y;
return d;
}
例题1:求解蓝桥杯一步之遥。
#include <iostream>
using namespace std;
//求解ax + by = gcd(a, b)的解,即求满足的x和y,并返回a和b的最大公约数。
int exgcd(int a, int b, int &x, int &y)
{
if (b == 0)
{
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int z = x;
x = y;
y = z - (a / b) * y;
return d;
}
int main()
{
int a, b, x, y;
a = 97, b = -127;
exgcd(a, b, x, y);
cout << x + y << endl;
return 0;
}
/* 答案为97 */
一步一步迭代。有
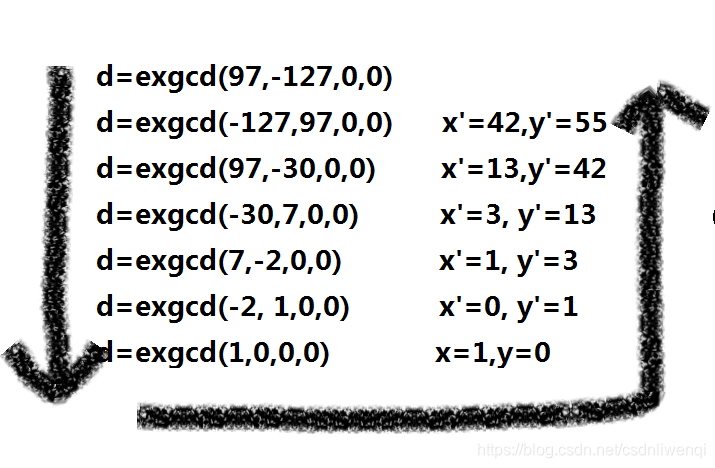




 该博客介绍了欧几里得算法(辗转相除法)用于求解最大公约数(GCD)的过程,并展示了如何通过迭代实现这一算法。博主通过一个具体的例子,展示了如何使用递归和迭代的方式找到97和-127的最大公约数,最后得出答案为97。此外,还提供了一个C++实现的exgcd函数,用于计算GCD并返回满足ax+by=GCD(a,b)的解。
该博客介绍了欧几里得算法(辗转相除法)用于求解最大公约数(GCD)的过程,并展示了如何通过迭代实现这一算法。博主通过一个具体的例子,展示了如何使用递归和迭代的方式找到97和-127的最大公约数,最后得出答案为97。此外,还提供了一个C++实现的exgcd函数,用于计算GCD并返回满足ax+by=GCD(a,b)的解。
















 1259
1259

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








