HDU4947(莫比乌斯反演 + 树状数组维护)

GCD Array

Time Limit: 11000/5500 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1445    Accepted Submission(s): 430

Problem Description

Teacher Mai finds that many problems about arithmetic function can be reduced to the following problem:

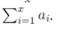
Maintain an array a with index from 1 to l. There are two kinds of operations:

  1. Add v to a _x for every x that gcd(x,n)=d.
  2. Query

 

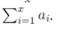
Input

There are multiple test cases, terminated by a line "0 0".

For each test case, the first line contains two integers l,Q(1<=l,Q<=5*10^4), indicating the length of the array and the number of the operations.

In following Q lines, each line indicates an operation, and the format is "1 n d v" or "2 x" (1<=n,d,v<=2*10^5,1<=x<=l).

 

Output

For each case, output "Case #k:" first, where k is the case number counting from 1.

Then output the answer to each query.

 

Sample Input

  
  

   
   6 4
1 4 1 2
2 5
1 3 3 3
2 3
0 0
  
  

 

Sample Output

  
  

   
   Case #1:
6
7
  
  

 

Author

xudyh

 

Source

2014 Multi-University Training Contest 8

解题思路：这题也是非常的巧妙，充分利用了莫比乌斯函数的一个性质，然后今后进行了一系列神奇的转换，最后还有一个巧妙的f函数来代替数组来间接求解。真的是好题。

我是参考这个人的思路：http://www.cnblogs.com/flipped/p/HDU4947.html

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 200000 + 10;
int N, Q;
int mu[maxn];
LL Tree[maxn];
vector<int> p[maxn];//约数
bool valid[maxn];
int prime[maxn];
void Mobius()
{
    int tot = 0;
    mu[1] = 1;
    memset(valid, true, sizeof(valid));
    p[1].clear();
    for(int i = 2; i < maxn; i++)
    {
        p[i].clear();
        if(valid[i])
        {
            mu[i] = -1;
            prime[++tot] = i;
        }
        for(int j = 1; j <= tot && i * prime[j] < maxn; j++)
        {
            valid[i * prime[j]] = false;
            if(i % prime[j] == 0)
            {
                mu[i * prime[j]] = 0;
                break;
            }
            mu[i * prime[j]] = -mu[i];
        }
    }
    for(int i = 1; i < maxn; i++)
    {
        for(int j = i; j < maxn; j += i)
        {
            p[j].push_back(i);
        }
    }
}
int lowbit(int x)
{
    return x&(-x);
}
void add(int loc, LL value)
{
    for(int i = loc; i <= N; i += lowbit(i))
    {
        Tree[i] += value;
    }
}
LL get(int loc)
{
    LL ans = 0;
    for(int i = loc; i >= 1; i -= lowbit(i))
    {
        ans += Tree[i];
    }
    return ans;
}
void init()
{
    memset(Tree, 0, sizeof(Tree));
}
int main()
{
    Mobius();
    int Case = 1;
    while(~scanf("%d%d", &N, &Q) && N && Q)
    {
        init();
        int type ,x, n, d;
        LL v;
        printf("Case #%d:\n", Case++);
        for(int i = 1; i <= Q; i++)
        {
            scanf("%d", &type);
            if(type == 1)
            {
                scanf("%d%d%lld", &n, &d, &v);
                if(n % d) continue;
                n /= d;
                for(int j = 0; j < p[n].size(); j++)
                {
                    int pp = p[n][j];
                    add(pp * d, (LL)mu[pp] * v);
                }
            }
            else
            {
                scanf("%d", &x);
                LL sum = 0;
                int nxt;
                for(int j = 1; j <= x; j = nxt + 1)
                {
                    nxt = min(x / (x / j), x);
                    sum += (get(nxt) - get(j - 1)) * (LL)(x / j);
                }
                printf("%lld\n", sum);
            }
        }
    }
    return 0;
}