关于训练DNN的一些技巧

前言

当使用DNN训练一个模型时，可能会出现模型在测试集中表现不佳的情况。这不一定是因为出现了过拟合，还有很大可能是训练的模型在训练集中表现就不是很好，因此，当测试准确性时，应该同时计算模型在测试集和训练集的损失，进而挑选出适合的模型。
例如下图，56层的DNN效果甚至可能差于20层的DNN，这可能是因为56层的DNN训练停止在了鞍点或者局部最小值点。

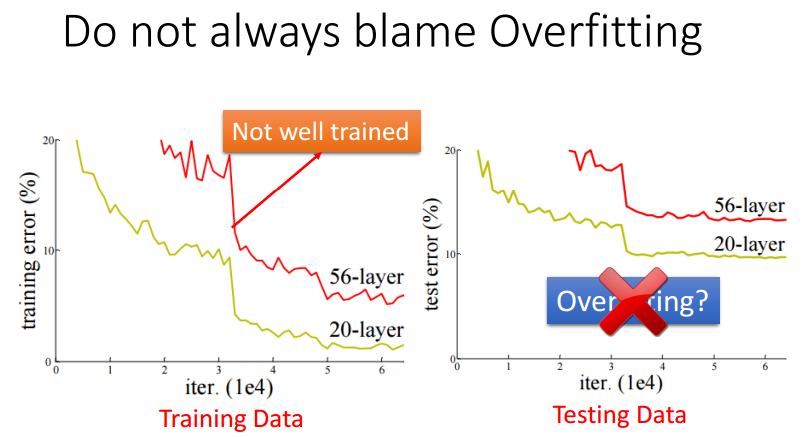
使DNN模型表现更好的诀窍有下面这几点：

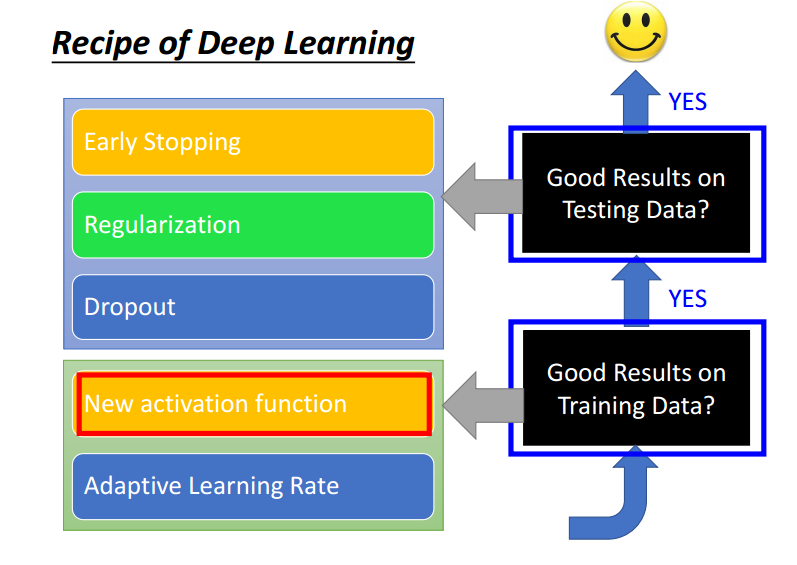
采用新的激活函数

在寻找新的激活函数之前，要先说明sigmoid函数作为激活函数会遇到的问题——vanish gradient proble，关于这个问题，详见 https://blog.youkuaiyun.com/fishmemory/article/details/53885691
梯度消失会导致当靠近输出层的权重已经被很大程度的更新时，靠近输入层的权重还没有被更动，此时得到的输出结果会收敛于靠近输入层的随机权重对应的结果，因此效果不会很理想。
因此，这里引入ReLU函数作为激活函数。

ReLU

关于为什么使用ReLU，其最主要的原因就是它能够解决深度神经网络中梯度消失问题（因为它是分段线性的）。

注意上面说的是分段线性，也就是说，对于小于等于零的数据，和大于零的数据，分开来看均为线性，但是二者放在一起便构成了非线性的了。
由于小于等于零的数据经过计算最终得到的值为 0，因此就相当于舍弃了这些为0 的节点，使得网络变得“更瘦”。

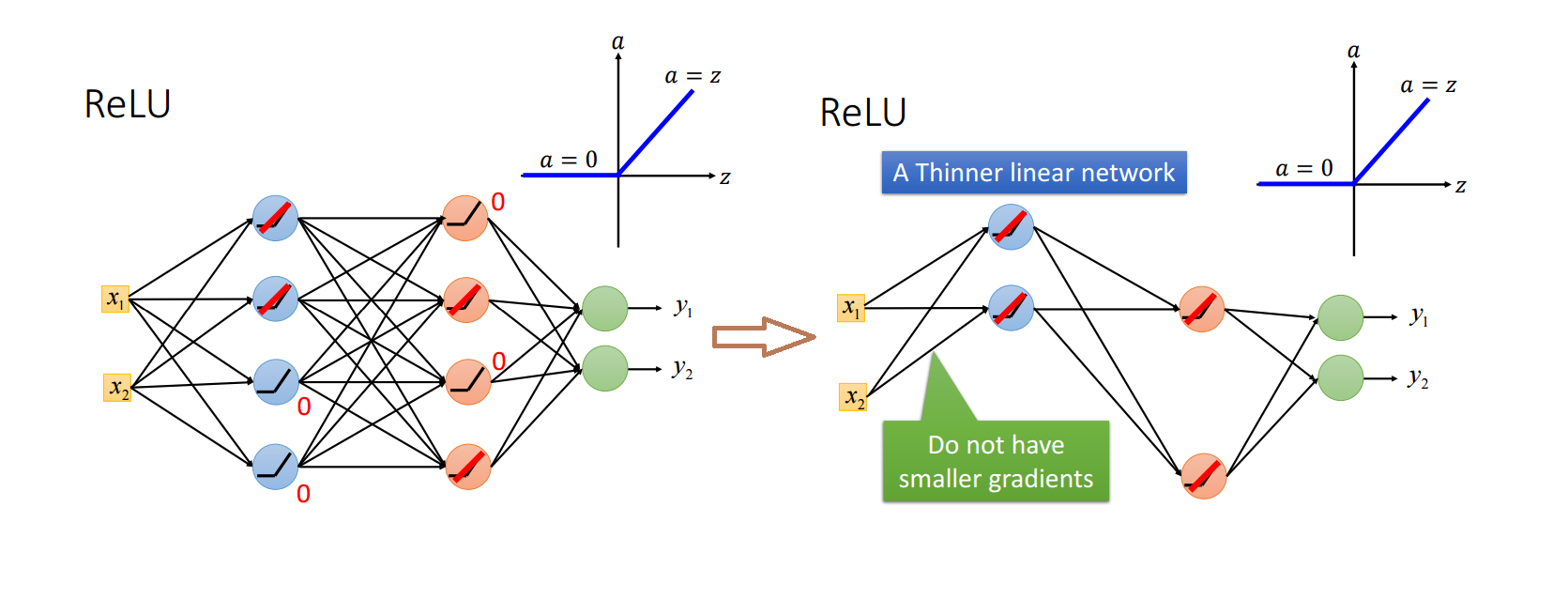
ReLU存在变体，如下：

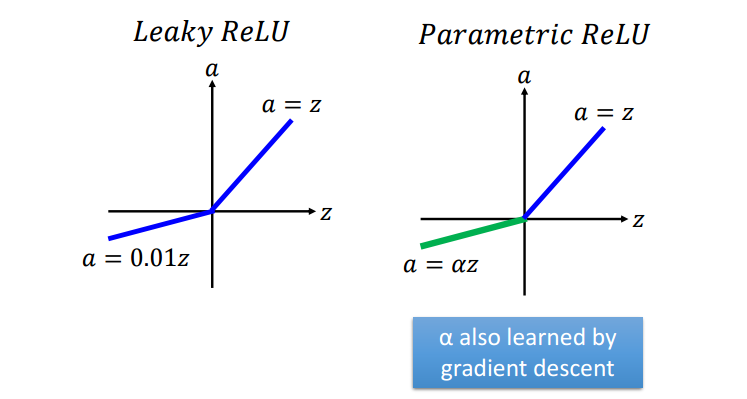
Maxout

事实上，ReLU相当于是Maxout的特殊情况。
Maxout的工作原理是：将每层的每 N 个节点划分为一组，每组取最大值作为下一层的输入。
例如下图将每层的每 2 个节点划分为一组取最大值，计算出最终结果。

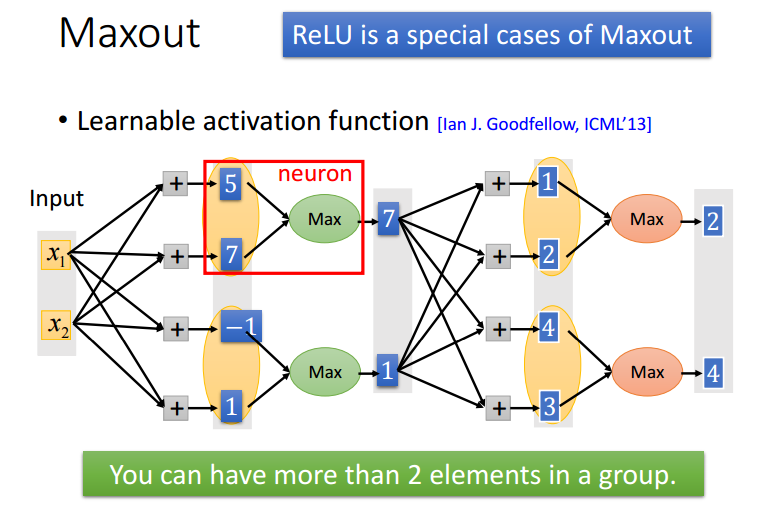
Maxout函数也是属于分段线性的，由于分段线性的特性，Maxout可以近似任何函数（可以将其想作微分）。近似的形状取决于每个group的大小：

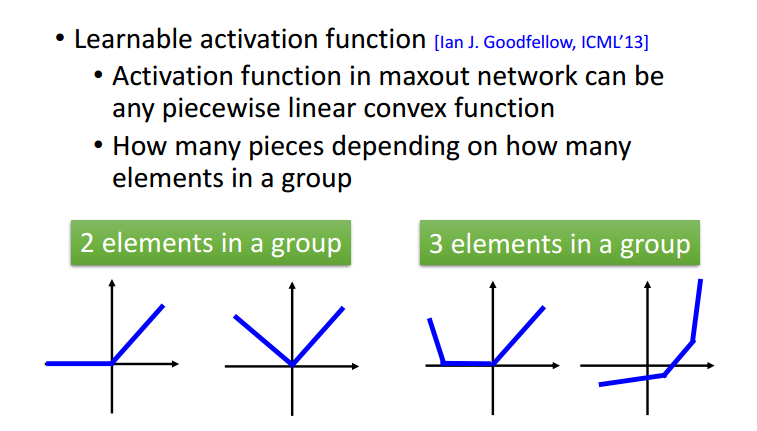
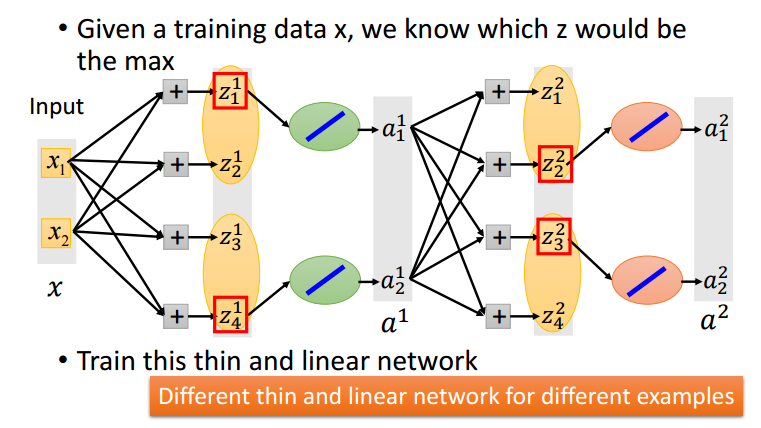
因为需要使用梯度下降更新权重，对maxout network求微分看似是一个问题，其实只需要每次计算最大值点的微分，而不去看其他点即可（训练集中不同数据作为输入得到的Maxout网络结构不同，因此基本每个结点的权重都会被更新到）。

（未完待续）