LeetCode-1.两数之和_在立即执行函数内定义构造函数,实现对两数的加减乘除运算。-优快云博客

本文深入探讨了解决两数之和问题的三种算法：暴力法、两遍哈希表及一遍哈希表。通过对比不同方法的效率，阐述了如何在数组中寻找两个数使它们的和等于特定目标值。适用于初学者理解基本算法原理。

描述：
在这里插入图片描述
分析：
（1）暴力法：

对每个元素，依次查找表中是否有另一元素，与这个元素之和为 $t a r g e t$ ，有则直接返回。
由于在比较一个元素与表中其他元素时，它之前的元素已经进行过比较，因此第二层循环的下标可以直接从第一层循环加一开始。

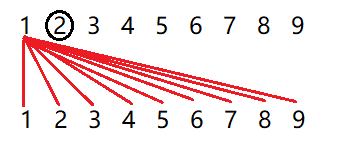
如图，在进行 $2$ 这个值的比较时，因为此前的 $1$ 已经和 $2$ 比较过，因此 $2$ 无需再和之前的元素比较。

for(int i = 0;i < size - 1;i++)
	for(int j = i + 1;j < size;j++)
		....

（2）两遍哈希表

下图来自官网解答
在这里插入图片描述

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int size = nums.size();
        map<int, int> mp;
        for(int i = 0;i < size;i++)
            mp[nums[i]] = i;
        for(int i = 0;i < size;i++){
            if(mp.count(target-nums[i]) && mp[target-nums[i]]!=i)
                return {i, mp[target-nums[i]]};
        }
        return {0, 0};
    }
};

（3）一遍哈希表

将上面的两层循环合并，改为检验一个元素前是否有满足条件的另一个元素。这样避免了同一元素的二倍恰好等于 $t a r g e t$ 时需要进行判断的情况。

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int size = nums.size();
        map<int, int> mp;
        for(int i = 0;i < size;i++){
            if(mp.count(target-nums[i]))
                return {mp[target-nums[i]], i};
            mp[nums[i]] = i;
        }
        return {0, 0};
    }
};