文章目录
断更两天我错了 真的错了
凸包
P2742 【模板】二维凸包
题目链接
如题，就是一道模板题啦
没啥好说的
AC代码：
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define vc pt
#define db double
#define rep(i,a,b) for(int i = (a);i <= (b);i ++)
#define _rep(i,a,b) for(int i = (a);i >= (b);i --)
using namespace std;
const int N = 1e5 + 10;
const db eps = 1e-8;
int dcmp(db x){if(fabs(x) <= eps) return 0;return x > 0 ? 1 : -1;}
struct pt{
db x,y;
pt(){}
pt(db x,db y): x(x),y(y) {}
}p[N],s[N];
pt operator - (pt a,pt b){return pt(a.x - b.x,a.y - b.y);}
pt operator + (pt a,pt b){return pt(a.x + b.x,a.y + b.y);}
pt operator * (pt a,db d){return pt(a.x * d,a.y * d);}
db operator * (pt a,pt b){return a.x * b.x + a.y * b.y;}
db len(vc a){return sqrt(a * a);}
db cs(vc a,vc b){return a.x * b.y - a.y * b.x;}
bool Acmp(pt a,pt b){
if(fabs(a.x - b.x) <= eps) return a.y < b.y;
return a.x < b.x;
}
int Andrew(pt p[],int n,pt s[]){
sort(p + 1,p + 1 + n,Acmp);
s[1] = p[1];
int m = 1;
rep(i,2,n){
while(m > 1 && cs(s[m] - s[m - 1],p[i] - s[m]) <= 0) m -- ;
s[++ m] = p[i];
}
int k = m;
_rep(i,n - 1,1){
while(m > k && cs(s[m] - s[m - 1],p[i] - s[m]) <= 0) m --;
s[++ m] = p[i];
}
if(n > 1) m --;
return m;
}
int main(){
int n,m;
scanf("%d",&n);
rep(i,1,n){scanf("%lf%lf",&p[i].x,&p[i].y);}
m = Andrew(p,n,s);
db ans = 0;
rep(i,1,m){ans += len(s[i] - s[i + 1]);}
printf("%.2f\n",ans);
return 0;
}
P3829 [SHOI2012]信用卡凸包
题目链接
好题！其实多动手画画图就能看出来
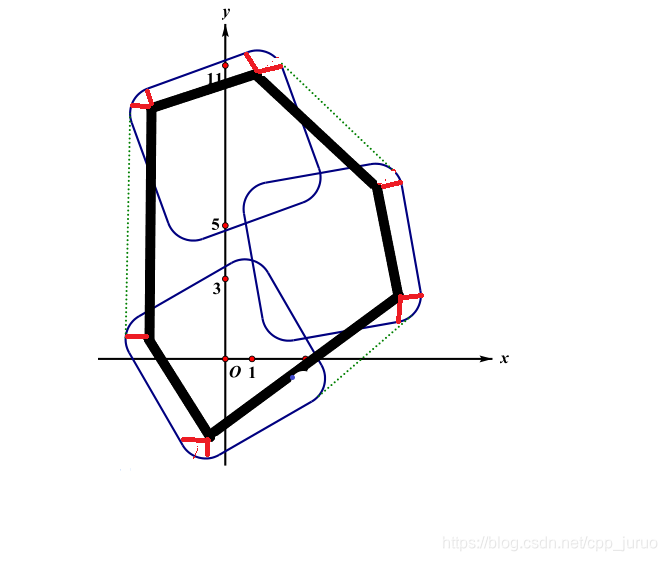
不难证明，其实就是圆心的凸包长度加上一个圆的周长
AC代码：
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define db double
using namespace std;
const int N = 1e6 + 10;
const db PI = acos(-1),eps = 1e-10;
struct pt{
db x,y;
pt(){}
pt(db x,db y) : x(x),y(y){}
}p[N],q[N];
pt operator + (pt a,pt b){return pt(a.x + b.x,a.y + b.y);}
pt operator - (pt a,pt b){return pt(a.x - b.x,a.y - b.y);}
pt operator * (pt a,db d){return pt(a.x * d,a.y * d);}
db operator * (pt a,pt b){return a.x * b.x + a.y * b.y;}
bool operator < (const pt& a,const pt& b){
return a.x == b.x ? a.y < b.y : a.x < b.x;
}
db cs(pt a,pt b){return a.x * b.y - a.y * b.x;}
db cs(pt a,pt b,pt c){return (b - a).x * (c - a).y - (b - a).y * (c - a).x;}
db len(pt a){return sqrt(a * a);}
pt rt(pt a,db t){
db c = cos(t),s = sin(t);
return pt(a.x * c - a.y * s, a.x * s + a.y * c);
}
int main(){
int n,cnt = 0;
db a,b,r,x,y,t;
scanf("%d%lf%lf%lf",&n,&a,&b,&r);
a /= 2,b /= 2;
for(int i = 1;i <= n;i ++){
scanf("%lf%lf%lf",&x,&y,&t);
pt cen = pt(x,y);
p[++ cnt] = rt(pt(b - r,a - r),t) + cen;
p[++ cnt] = rt(pt(b - r,r - a),t) + cen;
p[++ cnt] = rt(pt(r - b,r - a),t) + cen;
p[++ cnt] = rt(pt(r - b,a - r),t) + cen;
}
sort(p + 1, p + cnt + 1);
int m = 0;
for(int i = 1;i <= cnt;i ++){
while(m > 1 && cs(q[m - 1],q[m],p[i]) <= 0) m --;
q[++ m] = p[i];
}
int k = m;
for(int i = cnt - 1;i >= 1;i --){
while(m > k && cs(q[m - 1],q[m],p[i]) <= 0) m --;
q[++ m] = p[i];
}
db ans = 2 * PI * r;
for(int i = 1;i < m;i ++) ans += len(q[i] - q[i + 1]);
printf("%.2f\n",ans);
return 0;
}
旋转卡壳
P1452 [USACO03FALL]Beauty Contest G /【模板】旋转卡壳
题目链接
又是一道模板题呢
AC代码：
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 5e5 + 10;
int n,m;
struct Point{
int x,y;
Point(){}
Point(int x,int y) : x(x),y(y){}
int length(){
return x * x + y * y;
}
Point operator - (const Point& b)const{return Point(x - b.x,y - b.y);}
bool operator < (const Point& b){
if(x == b.x) return y < b.y;
return x < b.x;
}
};
int dis(Point& a,Point& b){
return (b - a).length();
}
int cross(Point& a,Point& b,Point& c){
return (b - a).x * (c - a).y - (b - a).y * (c - a).x;
}
Point p[N],st[N];
void Andrew(){
sort(p,p + n);
for(int i = 0;i < n;i ++){
while(m > 1 && cross(st[m - 2],st[m - 1],p[i]) <= 0) m --;
st[m ++] = p[i];
}
int k = m;
for(int i = n - 2;i >= 0;i --){
while(m > k && cross(st[m - 2],st[m - 1],p[i]) <= 0) m --;
st[m ++] = p[i];
}
if(n > 1) m --;
}
void Rotating_Calipers(){
int cur = 1;int ans = 0;
for(int i = 0;i < m;i ++){
while(cross(st[i],st[i + 1],st[cur]) < cross(st[i],st[i + 1],st[cur + 1]))
cur = (cur + 1) % m;
ans = max(ans,max(dis(st[i],st[cur]),dis(st[i + 1],st[cur])));
}
printf("%d\n",ans);
}
int main(){
scanf("%d",&n);
for(int i = 0;i < n;i ++) scanf("%d%d",&p[i].x,&p[i].y);
Andrew();
Rotating_Calipers();
}
P3187 [HNOI2007]最小矩形覆盖
题目链接
首先不难想到，最小矩形的一条边肯定与凸包的某一条边重合 那么我们就可以枚举凸包的每一条边然后旋转卡壳求一下对踵点 然后更新一下答案就行
记得防止输出负零（切记）
AC代码：
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#define db double
#define vc pt
using namespace std;
const int N = 5e4 + 10;
const db eps = 1e-8;
int dcmp(double x){return x < -eps ? -1 : x > eps;}
struct pt{
db x,y;
pt(){}
pt(db x,db y): x(x),y(y){}
bool operator < (const pt& b)const{return !dcmp(y - b.y) ? x < b.x : y < b.y;}
}p[N],s[N],t[5];
typedef pt vc;
vc operator + (vc a,vc b){return vc(a.x + b.x,a.y + b.y);}
vc operator - (pt a,pt b){return vc(a.x - b.x,a.y - b.y);}
vc operator * (vc a,db d){return vc(a.x * d,a.y * d);}
db operator * (vc a,vc b){return a.x * b.x + a.y * b.y;}
db cs(vc a,vc b){return a.x * b.y - a.y * b.x;}
db cs(pt a,pt b,pt c){return (b - a).x * (c - a).y - (b - a).y * (c - a).x;}
db len(vc a){return sqrt(a * a);}
int n,m;
bool Gcmp(pt a,pt b){
db k = cs(a - p[1],b - p[1]);
if(fabs(k) < eps) return len(p[1] - a) < len(p[1] - b);
return k > 0;
}
void Graham(){
for(int i = 2;i <= n;i ++) if(p[i] < p[1]) swap(p[i],p[1]);
sort(p + 2,p + n + 1,Gcmp);
s[++ m] = p[1];
for(int i = 2;i <= n;i ++){
while(m > 1 && cs(s[m] - s[m - 1],p[i] - s[m]) < eps) m --;
s[++ m] = p[i];
}
s[0] = s[m];
}
db ans = 1e60;
void solve(){
int l = 1,r = 1,p = 1;
db L,R,D,H;
for(int i = 0;i < m;i ++){
D = len(s[i] - s[i + 1]);
while(cs(s[i],s[i + 1],s[p + 1]) - cs(s[i],s[i + 1],s[p]) > - eps) p = (p + 1) % m;
while((s[i + 1] - s[i]) * (s[r + 1] - s[i]) - (s[i + 1] - s[i]) * (s[r] - s[i]) > -eps) r = (r + 1) % m;
if(i == 0) l = r;
while((s[i + 1] - s[i]) * (s[l + 1] - s[i]) - (s[i + 1] - s[i]) * (s[l] - s[i]) < eps) l = (l + 1) % m;
L = (s[i + 1] - s[i]) * (s[l] - s[i]) / D;
R = (s[i + 1] - s[i]) * (s[r] - s[i]) / D;
H = cs(s[i],s[i + 1],s[p]) / D;
if(H < 0) H = -H;
db tmp = (R - L) * H;
if(tmp < ans){
ans = tmp;
t[0] = s[i] + (s[i + 1] - s[i]) * (R / D);
t[1] = t[0] + (s[r] - t[0]) * (H / len(t[0] - s[r]));
t[2] = t[1] - (t[0] - s[i]) * ((R - L) / len(s[i] - t[0]));
t[3] = t[2] - (t[1] - t[0]);
}
}
}
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;i ++) scanf("%lf%lf",&p[i].x,&p[i].y);
Graham();
solve();
printf("%.5lf\n",ans);
int fir = 0;
for(int i = 1;i <= 3;i ++) if(t[i] < t[fir]) fir = i;
for(int i = 0;i <= 3;i ++)
printf("%.5lf %.5lf\n",fabs(t[(i + fir) % 4].x) > 1e-12?t[(i + fir) % 4].x : 0.00000,fabs(t[(i + fir) % 4].y) > 1e-12 ? t[(i + fir) % 4].y : 0.00000);
return 0;
}
半平面交
P3256 [JLOI2013]赛车
题目链接
就是在直角坐标系第一象限中画一下位移和时间图像 然后自己加上去四条直线求个半平面交就行 注意限度取大，精度取小
AC代码：
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define db long double
#define vc pt
using namespace std;
const int N = 1e5 + 10;
const long long lim = 1e18 + 10;
const db eps = 1e-18;
int n,m,cnt,num,l,r,ans[N];
db k[N],w[N];
int dcmp(db x){return x < -eps ? -1 : x > eps;}
struct pt{
db x,y;
pt(){}
pt(db x,db y) : x(x),y(y){}
}sta[N];
vc operator + (pt a,pt b){return vc(a.x + b.x,a.y + b.y);}
vc operator - (pt a,pt b){return vc(a.x - b.x,a.y - b.y);}
vc operator * (vc a,db d){return vc(a.x * d,a.y * d);}
db operator * (vc a,vc b){return a.x * b.x + a.y * b.y;}
db cs(vc a,vc b){return a.x * b.y - a.y * b.x;}
struct line{
pt x,y;int id;
double deg;
line(){}
line(pt x,pt y,int id) : x(x),y(y),id(id) {deg = atan2((y - x).x,(y - x).y);}
}L[N],q[N];
bool oR(pt p,line a){return dcmp(cs(p - a.x,a.y - a.x) - eps) > 0;}
pt lip(line a,line b){//line_intersecton_point
vc v = a.y - a.x, u = b.y - b.x,w = a.x - b.x;
db t = cs(w,u) / cs(u,v);
return a.x + v * t;
}
bool HPIcmp(line a,line b){
if(dcmp(a.deg - b.deg) == 0) return oR(b.x,a);
return a.deg < b.deg;
}
int HPI(){//half_plane_intersection
sort(L + 1,L + cnt + 1,HPIcmp);
l = 1,r = 1;q[1] = L[1];
for(int i = 2;i <= cnt;i ++){
if(!dcmp(L[i].deg - L[i - 1].deg)) continue;
while(l < r && oR(sta[r - 1],L[i])) r --;
while(l < r && oR(sta[l],L[i])) l ++;
q[++ r] = L[i];
if(l < r) sta[r - 1] = lip(q[r],q[r - 1]);
}
while(l < r && oR(sta[r - 1],q[l])) r --;
while(l < r && oR(sta[l],q[r])) l ++;
sta[r] = lip(q[l],q[r]);
if(r - l + 1 <= 1) return 0;
return r - l + 1;
}
void solve(){
for(int i = l;i <= r;i ++){
for(int j = 1;j <= n;j ++){
if(w[j] == w[q[i].id] && k[j] == k[q[i].id])
ans[++ num] = j;
}
}
sort(ans + 1, ans + num + 1);
cout << num << endl;
for(int i = 1;i <= num;i ++) cout << ans[i] << " ";
cout << endl;
}
int main(){
cin >> n;
for(int i = 1;i <= n;i ++) cin >> w[i];
for(int i = 1;i <= n;i ++) cin >> k[i];
pt a = pt(0,0),b = pt(lim,0);
pt c = pt(lim,lim),d = pt(0,lim);
L[++ cnt] = line(a,b,0),L[++ cnt] = line(b,c,0);
L[++ cnt] = line(c,d,0),L[++ cnt] = line(d,a,0);
for(int i = 1;i <= n;i ++){
pt a = pt(0,w[i]),b = pt(1,w[i] + k[i]);
L[++ cnt] = line(a,b,i);
}
m = HPI();
solve();
return 0;
}
P2600 [ZJOI2008]瞭望塔
题目链接
看到n<=300 直接暴力
首先枚举一下每一个点求一个最小高度
再枚举一下任意两条直线的交点求最小高度
可能有人会想（比如我）诶任意两条直线交点不就包含每一个点了吗
那起点和终点呢…
AC代码：
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#define rep(i,a,b) for(int i = (a);i <= (b);i ++)
#define _rep(i,a,b) for(int i = (a);i >= (b);i --)
#define db double
using namespace std;
const int N = 310;
const db INF = 99999999999.0;
struct line{
db k,b;
line(){}
line(db k,db b) : k(k),b(b) {}
}l[N];
int n;db x[N],y[N];
db work(db x){
db ans = 0;
rep(i,1,n - 1) ans = max(ans,l[i].k * x + l[i].b);
return ans;
}
int main(){
scanf("%d",&n);
rep(i,1,n) scanf("%lf",&x[i]);
rep(i,1,n) scanf("%lf",&y[i]);
rep(i,1,n - 1){
db k = (y[i + 1] - y[i]) / (x[i + 1] - x[i]);
db b = - k * x[i] + y[i];
l[i] = line(k,b);
}
db ans = INF;
rep(i,1,n) ans = min(ans,work(x[i]) - y[i]);
rep(i,1,n - 1){
rep(j,i + 1,n - 1){
db o = (l[j].b - l[i].b) / (l[i].k - l[j].k);
rep(k,1,n - 1){
if(x[k] <= o && o <= x[k + 1]){
ans = min(ans,work(o) - l[k].k * o - l[k].b);
}
}
}
}
printf("%.3f",ans);
return 0;
}
P4196 [CQOI2006]凸多边形 /【模板】半平面交
题目链接
怎么又是模板题 难的又不会做只能做模板题啦
AC代码：
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
typedef double db;
const int N = 1e3 + 10;
const double eps = 1e-10;
int n,m,sum;
struct pt{
db x,y;
pt () {}
pt(db x,db y) : x(x),y(y) {}
void rd(){scanf("%lf%lf",&x,&y);}
}p[N],q[N];
typedef pt vc;
vc operator + (pt a,pt b){return vc(a.x + b.x,a.y + b.y);}
vc operator - (pt a,pt b){return vc(a.x - b.x,a.y - b.y);}
vc operator * (vc a,db d){return vc(a.x * d,a.y * d);}
db operator * (vc a,vc b){return a.x * b.x + a.y * b.y;}
db cross(vc a,vc b){return a.x * b.y - a.y * b.x;}
struct line{
pt p;vc v;
db deg;
line(){}
line(pt p,vc v) : p(p),v(v){deg = atan2(v.y,v.x);}
bool operator < (const line& b)const{return deg < b.deg;}
}l[N],s[N];
pt lip(line a,line b){//line_intersection_point
vc u = a.p - b.p;
db t = cross(u,b.v) / cross(b.v,a.v);
return a.p + a.v * t;
}
int hd,tl;
void hpi(){//half_plane_intersection
sort(l + 1,l + sum + 1);
hd = 1,tl = 1;
s[hd] = l[1];
for(int i = 2;i <= sum;i ++){
while(hd < tl && cross(l[i].v,q[tl - 1] - l[i].p) <= eps) tl --;
while(hd < tl && cross(l[i].v,q[hd] - l[i].p) <= eps) hd ++;
s[++ tl] = l[i];
if(fabs(cross(s[tl].v,s[tl - 1].v)) <= eps){
tl --;
if(cross(s[tl].v,l[i].p - s[tl].p) > eps) s[tl] = l[i];
}
if(hd < tl){
q[tl - 1] = lip(s[tl - 1],s[tl]);
}
}
while(hd < tl && cross(s[hd].v,q[tl - 1] - s[hd].p) <= eps) tl --;
if(tl - hd <= 1)return;
q[tl] = lip(s[hd],s[tl]);
}
void solve(){
db ans = 0;
for(int i = hd;i <= tl;i ++){
int tt = i + 1;
if(i == tl) tt = hd;
ans += cross(q[i],q[tt]);
}
printf("%.3f\n",ans / 2);
}
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;i ++){
scanf("%d",&m);
for(int j = 1;j <= m;j ++) p[j].rd();
for(int j = 1;j <= m;j ++){
int tt = j + 1;
if(j == m) tt = 1;
l[++ sum] = line(p[j],p[tt] - p[j]);
}
}
hpi();
solve();
return 0;
}
图论
P2661 [NOIP2015 提高组] 信息传递
题目链接
看到这种题就不要想着爆搜了
用点技巧 比如并查集判环
AC代码：
#include<iostream>
#include<cstdio>
#define rep(i,a,b) for(int (i) = (a);(i) <= (b);(i) ++)
using namespace std;
const int N = 2e5 + 10;
int fa[N];
int getf(int x,int& cnt){
cnt ++;
return x == fa[x] ? x : getf(fa[x],cnt);
}
int n;
int main(){
scanf("%d",&n);
rep(i,1,n) fa[i] = i;
int ans = 0x3f3f3f3f;
rep(i,1,n){
int cnt = 0,x;
scanf("%d",&x);
if(getf(x,cnt) == i) ans = min(ans,cnt);
else fa[i] = x;
}
printf("%d",ans);
return 0;
}
P2921 [USACO08DEC]Trick or Treat on the Farm G
题目链接
两道题好像啊 但是我还是不会
看了题解真的好强
就是用一个h[]数组记录一下一个环内的糖果数
因为一只牛想要停下来必须得进入某一个环里
s[]记录到达某个房间的糖果数就好了
如果一个点被经过了两次，那么这个环的糖果数就是当前减去s[now]
具体细节看代码，回溯的时候可以把环内的节点都做一下标记，即更新h[]数组
AC代码：
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define rep(i,a,b) for(int (i) = (a);(i) <= (b);(i) ++)
using namespace std;
const int N = 1e5 + 10;
int d[N],h[N],s[N],vis[N],fl;
int dfs(int now,int sum){
if(h[now]) return sum - 1 + h[now];
if(vis[now]){
h[now] = sum - s[now];
fl = now;
return sum - 1;
}
vis[now] = true;
s[now] = sum;
int ans = dfs(d[now],sum + 1);
if(fl){
if(fl == now) fl = 0;
else h[now] = h[fl];
}
else h[now] = h[d[now]] + 1;
vis[now] = false;
return ans;
}
int main(){
int n;scanf("%d",&n);
rep(i,1,n) scanf("%d",&d[i]);
rep(i,1,n) printf("%d\n",dfs(i,1));
return 0;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
