LeetCode Hot 100题之 No.62 不同路径

最新推荐文章于 2024-07-20 15:35:45 发布

原创最新推荐文章于 2024-07-20 15:35:45 发布 · 134 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #动态规划 #算法 #数据结构

LeetCode Hot 100 专栏收录该内容

86 篇文章

订阅专栏

该博客详细介绍了如何使用动态规划解决机器人在mxn网格中从左上角到达右下角的不同路径数问题。通过建立递推关系f(i,j)=f(i,j−1)+f(j−1,i)，并初始化边缘位置的路径数为1，逐步计算出每个位置的路径数量，最后得出(m-1,n-1)位置的值作为答案。整个过程采用双重for循环实现，时间复杂度为O(m*n)。

题目：
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？
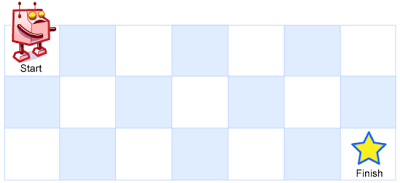
在这里插入图片描述
示例1：
输入：m = 3, n = 7
输出：28

示例2：
输入：m = 3, n = 2
输出：3

示例3：
输入：m = 7, n = 3
输出：28

示例4：
输入：m = 3, n = 3
输出：6

这是一道典型的动态规划题，动态规划题目的特点是：
每一个中间结果都只与其相邻的几个之前的结果有关。

所以，求解动态规划问题是一个从前往后的求解过程：

先确定如何从某几个当前结果求出与之相邻的下一个结果。（也就是找到递推关系）
确定初始值。（已知的可以确定的最开始的几个值）。
确定求解结束的条件。

现在来分析这个题目，我们先从求某个中间结果开始。比如我现在想知道从左上角走到第（i,j）位置上的格子总共有多少条路。因为机器人只能往右和下这两个方向走，所以我只能从（i,j）左侧和上方的这两个格子（也就是（i,j-1）和(i-1,j)）到达（i,j)。而且从（i,j-1）和（i-1,j）这两个格子到达（i,j）不会产生新的支路。所以从左上角到（i,j）的路的数量，等于从左上角到（i,j-1）和(i-1,j)的路的数量之和。我们用f(i，j)来表示路的数量，那么递推关系即为：

$f (i, j) = f (i, j - 1) + f (j - 1, i)$

那么我们就能确定，每个位置的路径 = 该位置左边的路径 + 该位置上边的路径。

到此，递推关系确定了。

以m=3,n=7为例,我们用一个3*7的二维矩阵来保存从左上角到达每个位置的路线数量。我们可以确定左侧和上侧边缘位置的初始值。到达这些格子的路线只有一种，所以全部初始化为1。
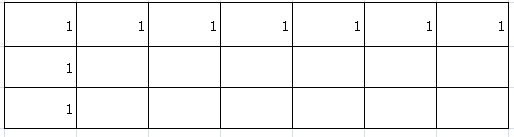
在这里插入图片描述
然后，我们可以从左到右，从上到下依次遍历这个二维矩阵。

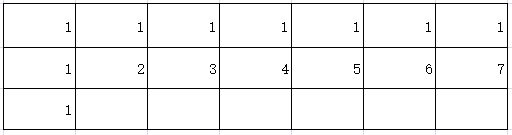
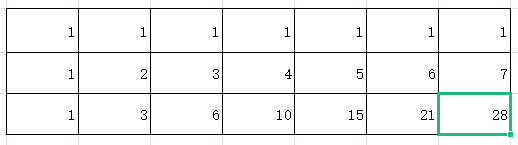
当第（m-1,n-1）处的值生成出来，对二维矩阵的遍历也完成了。我们返回（m-1,n-1）就是该题的最终结果了。

整个过程可以用一个很简单的双重for循环来解决。时间复杂度为O(m*n)。

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] block = new int[m][];
        for(int i=0;i<m;i++)//初始化，这部分还可以再优化
        {
            block[i] = new int[n];    
            for(int j=0;j<n;j++)
            {
                if(i==0||j==0)
                    block[i][j]=1;
            }
        }
        block[0][0]=1;
        for(int i=0;i<m;i++)//生成每一个位置的路径数量
        {
            for(int j=0;j<n;j++)
            {
                if(i!=0&&j!=0)
                {
                    block[i][j]=block[i][j-1]+block[i-1][j];
                }
            }
        }
        return block[m-1][n-1];       
         

    }
}