leetCode Hot 100 No.647 回文子串

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：“abc”
输出：3
解释：三个回文子串: “a”, “b”, “c”
示例 2：

输入：“aaa”
输出：6
解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

思路：
动态规划方法。
写出递推公式：
一个字符串是否为回文串，则只需判断它两端的字符是否相等和其中间的字符子串是否为回文串。
如果两端字符相等且中间字符子串是回文串，则该字符串为回文串。
即，判断一个起始位置为i,终止位置为j的字符串s(i,j)是否为回文串，只需判断i，j位置的字符是否相等，且s（i+1，j-1）是否为回文串。
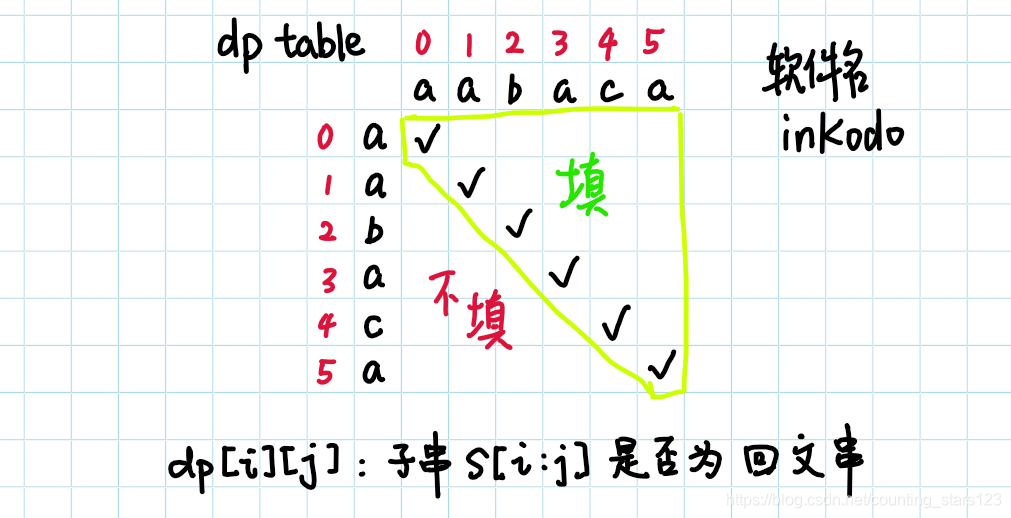
我们可以将s（i,j）是否为回文串写在一个二维数组里。
用一个二重循环即可完成。最终这个二维数组中有多少个√（或有多少个元素为true），这个字符串就有多少个回文子串。

class Solution {
    public int countSubstrings(String s) {
        int n = s.length();
        boolean[][] state = new boolean[n][n];
        int num = 0;
        for(int j=0;j<n;j++)
        {
            for(int i=0;i<=j;i++)
            {
                if(i==j)
                    state[i][j] = true;
                if(j-i==1)
                {
                    state[i][j] = (s.charAt(i)==s.charAt(j));
                }
                if(j-i>1)
                {
                    state[i][j] = (s.charAt(i)==s.charAt(j))&&state[i+1][j-1];
                }
                if(state[i][j])
                    num++;
            }
        }
        return num;
  
    }
}

思路2：
中心扩展法：我们选定一个中心，向两边拓展，只要两端字符相等就继续拓展。每扩展一次，回文串的总个数就加一。
注意：对于一个奇数长度的回文串，如abcba，那么我们只要将中心定在c处就能遍历出这个回文串。但是对一个偶数长度的回文串，如abba，那么我们的中心就不能是单个的字符，需要变为两个字符bb,从bb两侧扩展就能遍历出abba。
我们可以遍历两趟，第一趟是单个字符为中心，第二趟为双字符为中心。
但是也可以用一趟来解决。我们容易知道对于一个长度为n的字符串，其单个字符中心个数为n, 其双字符中心个数为n-1。那么，其所有字符中心总数为2n-1。
我们用left和right指针来指向字符中心，如果是单个字符中心，left==right, 如果是双字符中心, right=left+1。
用一个center从0到2n-1遍历，每次left=center/2, right = center%2+left
当center为偶数的时候，left==right，当center为奇数的时候，right= left+1
然后left和right指针不断向外拓展。每扩展一次，回文串的总个数就加一。最后返回总个数即可。

class Solution {
    public int countSubstrings(String s) {
        int ans = 0;
        for(int center = 0;center<2*s.length()-1;center++)
        {
            int left = center/2;
            int right = left+center%2;
            while(left>=0&&right<=s.length()-1&&s.charAt(left)==s.charAt(right))
            {
                left--;
                right++;
                ans++;
            }
            
        }
        return ans;
    }
}