数项级数
什么是数项级数?
数项级数是无穷多个实数依次相加的数学表达式,是“有限项和”的极限推广
给定一个无穷实数列u1,u2,u3,…,un,…u_1, u_2, u_3, \dots, u_n, \dotsu1,u2,u3,…,un,…,将其所有项依次相加的表达式:
∑n=1∞un=u1+u2+u3+⋯+un+…\sum_{n=1}^{\infty} u_n = u_1 + u_2 + u_3 + \cdots + u_n + \dots∑n=1∞un=u1+u2+u3+⋯+un+…
称为数项级数(简称“级数”),其中unu_nun是级数的一般项(或“通项”)
级数的收敛与发散的定义
部分和数列的定义:取级数的前nnn项相加,得到的和Sn=u1+u2+⋯+unS_n = u_1 + u_2 + \dots + u_nSn=u1+u2+⋯+un,称为级数的前nnn项部分和(形成新的数列{Sn}\{S_n\}{Sn},即“部分和数列”)
引入了部分和数列之后,我们就能用级数对应的部分和数列极限是否存在,来定义级数的发散与收敛
级数收敛与发散的定义:
- 若部分和数列{Sn}\{S_n\}{Sn}的极限存在,即limn→∞Sn=S\lim_{n \to \infty} S_n = Slimn→∞Sn=S(SSS是有限实数),则称级数∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞un收敛,且其和为SSS,记为∑n=1∞un=S\sum_{n=1}^{\infty} u_n = S∑n=1∞un=S;
- 若部分和数列{Sn}\{S_n\}{Sn}的极限不存在(或极限为±∞\pm\infty±∞),则称级数∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞un发散(发散级数没有“和”)。
级数收敛与发散的经典案例
-
收敛案例:等比级数(几何级数)∑n=0∞aqn=a+aq+aq2+…\sum_{n=0}^{\infty} aq^n = a + aq + aq^2 + \dots∑n=0∞aqn=a+aq+aq2+…(a≠0a \neq 0a=0):
部分和Sn=a⋅1−qn+11−qS_n = a \cdot \frac{1 - q^{n+1}}{1 - q}Sn=a⋅1−q1−qn+1(q≠1q \neq 1q=1)。- 当∣q∣<1|q| < 1∣q∣<1时,limn→∞qn+1=0\lim_{n \to \infty} q^{n+1} = 0limn→∞qn+1=0,故limn→∞Sn=a1−q\lim_{n \to \infty} S_n = \frac{a}{1 - q}limn→∞Sn=1−qa,级数收敛;
- 当∣q∣≥1|q| \geq 1∣q∣≥1时,limn→∞Sn\lim_{n \to \infty} S_nlimn→∞Sn不存在,级数发散。
-
发散案例:调和级数∑n=1∞1n=1+12+13+…\sum_{n=1}^{\infty} \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \dots∑n=1∞n1=1+21+31+…:
部分和Sn=1+12+⋯+1nS_n = 1 + \frac{1}{2} + \dots + \frac{1}{n}Sn=1+21+⋯+n1,其极限为+∞+\infty+∞(可通过“积分放缩”证明),故级数发散。
给你一个数项级数,如何判断它是收敛还是发散呢?
第一步:先验证“收敛的必要条件”(如果一个级数连收敛的必要条件都不满足,那这个级数肯定不收敛,肯定是发散的)
对任意数项级数∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞un,若一般项的极限不为0,则级数必发散(这是“收敛的必要条件”,而非充分条件):
若 limn→∞un≠0⇒∑n=1∞un 发散\text{若 } \lim_{n \to \infty} u_n \neq 0 \quad \Rightarrow \quad \sum_{n=1}^{\infty} u_n \text{ 发散}若 limn→∞un=0⇒∑n=1∞un 发散
-
注意:若limn→∞un=0\lim_{n \to \infty} u_n = 0limn→∞un=0,级数仍可能发散(如调和级数∑1n\sum \frac{1}{n}∑n1,虽limn→∞1n=0\lim_{n \to \infty} \frac{1}{n} = 0limn→∞n1=0,但级数发散),需进一步用其他方法判断。
-
案例:级数∑n=1∞nn+1\sum_{n=1}^{\infty} \frac{n}{n+1}∑n=1∞n+1n,因limn→∞nn+1=1≠0\lim_{n \to \infty} \frac{n}{n+1} = 1 \neq 0limn→∞n+1n=1=0,直接判断发散。
第二步:根据级数类型选择针对性方法
级数按unu_nun符号的特征可分为三类:正项级数(每一项都是正数)、交错级数(任意相邻两项的符号相反)、任意项级数(每一项的符号任意)
对于不同类型的数项级数,我们有不同的针对性方法来判断它们是否收敛
,判断方法各有侧重:
类型1:正项级数(un≥0u_n \geq 0un≥0对所有nnn成立)
正项级数的核心性质:部分和数列{Sn}\{S_n\}{Sn}单调递增(因每加一项都是非负数)。根据“单调有界数列必有极限”,正项级数收敛的充要条件是“部分和数列有上界”。基于此,衍生出以下常用判别法:
| 判别法 | 核心思想 | 适用场景 |
|---|---|---|
| 比较判别法 | 若0≤un≤vn0 \leq u_n \leq v_n0≤un≤vn(对所有n≥Nn \geq Nn≥N): 1. 若∑vn\sum v_n∑vn收敛,则∑un\sum u_n∑un收敛; 2. 若∑un\sum u_n∑un发散,则∑vn\sum v_n∑vn发散。 | 已知一个“基准级数”(如等比级数、p-级数)的敛散性,用于比较未知级数。 |
| 比较判别法的极限形式 | 若limn→∞unvn=l\lim_{n \to \infty} \frac{u_n}{v_n} = llimn→∞vnun=l(vn>0v_n > 0vn>0): 1. 若0<l<+∞0 < l < +\infty0<l<+∞,则∑un\sum u_n∑un与∑vn\sum v_n∑vn同敛散; 2. 若l=0l = 0l=0,且∑vn\sum v_n∑vn收敛,则∑un\sum u_n∑un收敛; 3. 若l=+∞l = +\inftyl=+∞,且∑vn\sum v_n∑vn发散,则∑un\sum u_n∑un发散。 | 避免“逐项比较”的繁琐,只需计算极限,适用范围更广。 |
| 比值判别法(达朗贝尔判别法) | 若limn→∞un+1un=ρ\lim_{n \to \infty} \frac{u_{n+1}}{u_n} = \rholimn→∞unun+1=ρ(un>0u_n > 0un>0): 1. 若ρ<1\rho < 1ρ<1,则∑un\sum u_n∑un收敛; 2. 若ρ>1\rho > 1ρ>1(或ρ=+∞\rho = +\inftyρ=+∞),则∑un\sum u_n∑un发散; 3. 若ρ=1\rho = 1ρ=1,判别法失效(需换其他方法)。 | 一般项含“阶乘”“指数”(如n!n!n!、2n2^n2n)的正项级数,极限易计算。 |
| 根值判别法(柯西判别法) | 若limn→∞unn=ρ\lim_{n \to \infty} \sqrt[n]{u_n} = \rholimn→∞nun=ρ(un≥0u_n \geq 0un≥0): 1. 若ρ<1\rho < 1ρ<1,则∑un\sum u_n∑un收敛; 2. 若ρ>1\rho > 1ρ>1(或ρ=+∞\rho = +\inftyρ=+∞),则∑un\sum u_n∑un发散; 3. 若ρ=1\rho = 1ρ=1,判别法失效。 | 一般项含“n次幂”(如(1+1n)n(1+\frac{1}{n})^n(1+n1)n、(n2n+1)n(\frac{n}{2n+1})^n(2n+1n)n)的正项级数。 |
| 积分判别法 | 若un=f(n)u_n = f(n)un=f(n),且f(x)f(x)f(x)在[1,+∞)[1, +\infty)[1,+∞)上“非负、连续、单调递减”: 则∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞un与反常积分∫1+∞f(x)dx\int_{1}^{+\infty} f(x) dx∫1+∞f(x)dx同敛散。 | 一般项为“可积函数值”的级数(如 p-级数∑1np\sum \frac{1}{n^p}∑np1,可通过积分∫1+∞1xpdx\int_{1}^{+\infty} \frac{1}{x^p} dx∫1+∞xp1dx判别)。 |
- 重要基准级数:p-级数∑n=1∞1np\sum_{n=1}^{\infty} \frac{1}{n^p}∑n=1∞np1:
- 当p>1p > 1p>1时,收敛(如∑1n2\sum \frac{1}{n^2}∑n21收敛);
- 当p≤1p \leq 1p≤1时,发散(如p=1p=1p=1时的调和级数)。
类型2:交错级数(一般项正负交替,形如∑n=1∞(−1)n−1un\sum_{n=1}^{\infty} (-1)^{n-1} u_n∑n=1∞(−1)n−1un或∑n=1∞(−1)nun\sum_{n=1}^{\infty} (-1)^n u_n∑n=1∞(−1)nun,其中un>0u_n > 0un>0)
核心判别法:莱布尼茨判别法(充分不必要条件):
若交错级数∑n=1∞(−1)n−1un\sum_{n=1}^{\infty} (-1)^{n-1} u_n∑n=1∞(−1)n−1un满足以下两个条件,则级数收敛:
- 数列{un}\{u_n\}{un}单调递减:un+1≤unu_{n+1} \leq u_nun+1≤un(对所有n≥Nn \geq Nn≥N);
- 一般项的极限为0:limn→∞un=0\lim_{n \to \infty} u_n = 0limn→∞un=0。
- 案例:交错调和级数∑n=1∞(−1)n−11n=1−12+13−14+…\sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \dots∑n=1∞(−1)n−1n1=1−21+31−41+…:
满足un=1nu_n = \frac{1}{n}un=n1单调递减且limn→∞1n=0\lim_{n \to \infty} \frac{1}{n} = 0limn→∞n1=0,故收敛(但其绝对值级数∑1n\sum \frac{1}{n}∑n1发散,属于“条件收敛”)。
类型3:任意项级数(一般项可正、可负、可零)
任意项级数的敛散性需区分“绝对收敛”和“条件收敛”:
- 绝对收敛:若级数的“绝对值级数”∑n=1∞∣un∣\sum_{n=1}^{\infty} |u_n|∑n=1∞∣un∣收敛,则原级数∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞un必收敛,称为绝对收敛;
- 条件收敛:若级数∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞un收敛,但绝对值级数∑∣un∣\sum |u_n|∑∣un∣发散,则称为条件收敛。
-
判断逻辑:
先判断绝对值级数∑∣un∣\sum |u_n|∑∣un∣的敛散性(用正项级数的判别法,如比值、根值法):- 若∑∣un∣\sum |u_n|∑∣un∣收敛 → 原级数绝对收敛;
- 若∑∣un∣\sum |u_n|∑∣un∣发散 → 再判断原级数本身是否收敛(如交错级数用莱布尼茨判别法,或其他方法),若原级数收敛则为条件收敛,否则发散。
-
案例:级数∑n=1∞(−1)nn2\sum_{n=1}^{\infty} \frac{(-1)^n}{n^2}∑n=1∞n2(−1)n:
绝对值级数∑1n2\sum \frac{1}{n^2}∑n21是p=2>1的p-级数,收敛 → 原级数绝对收敛。
判断抽象级数的敛散性
判断抽象级数的敛散性的经典反例
让我们记住这个例子:∑n=1∞(−1)n1n\sum\limits_{n=1}^{\infty} (-1)^n \frac{1}{\sqrt{n}}n=1∑∞(−1)nn1收敛。一个例子可以打败百分之八十的假命题
剩下百分之二十,再想想这个例子:∑n=2∞(−1)n1lnn\sum\limits_{n=2}^{\infty} (-1)^n \dfrac{1}{\ln n}n=2∑∞(−1)nlnn1收敛,但∑n=2∞1nlnn\sum\limits_{n=2}^{\infty} \dfrac{1}{n \ln n}n=2∑∞nlnn1发散
下面就是使用的示例
注意,下面写的都是假命题!
-
若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞∣un∣\sum\limits_{n=1}^{\infty} |u_n|n=1∑∞∣un∣收敛
- 反例:∑n=1∞(−1)n1n\sum\limits_{n=1}^{\infty} (-1)^n \frac{1}{n}n=1∑∞(−1)nn1收敛,但∑n=1∞1n\sum\limits_{n=1}^{\infty} \frac{1}{n}n=1∑∞n1发散
-
若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞un2\sum\limits_{n=1}^{\infty} u_n^2n=1∑∞un2收敛
- 反例:∑n=1∞(−1)n1n\sum\limits_{n=1}^{\infty} (-1)^n \frac{1}{\sqrt{n}}n=1∑∞(−1)nn1收敛,但∑n=1∞1n\sum\limits_{n=1}^{\infty} \frac{1}{n}n=1∑∞n1发散
-
若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,∑n=1∞unun+1\sum\limits_{n=1}^{\infty} u_n u_{n+1}n=1∑∞unun+1收敛
- 反例:un=(−1)n1nu_n = (-1)^n \dfrac{1}{\sqrt{n}}un=(−1)nn1,unun+1=(−1)n1n(−1)n+11n+1=−1n(n+1)\quad u_n u_{n+1} = (-1)^n \dfrac{1}{\sqrt{n}} (-1)^{n+1} \dfrac{1}{\sqrt{n+1}} = -\dfrac{1}{\sqrt{n(n+1)}}unun+1=(−1)nn1(−1)n+1n+11=−n(n+1)1,∑n=1∞unun+1\sum\limits_{n=1}^{\infty} u_n u_{n+1}n=1∑∞unun+1发散
-
若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞(−1)nunn\sum\limits_{n=1}^{\infty} (-1)^n \dfrac{u_n}{n}n=1∑∞(−1)nnun收敛
- 反例:∑n=2∞(−1)n1lnn\sum\limits_{n=2}^{\infty} (-1)^n \dfrac{1}{\ln n}n=2∑∞(−1)nlnn1收敛,但∑n=2∞1nlnn\sum\limits_{n=2}^{\infty} \dfrac{1}{n \ln n}n=2∑∞nlnn1发散
具体例子

① 若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞∣un∣\sum\limits_{n=1}^{\infty} |u_n|n=1∑∞∣un∣不定
- 例如∑n=1∞(−1)n1n\sum\limits_{n=1}^{\infty} (-1)^n \frac{1}{n}n=1∑∞(−1)nn1收敛,但∑n=1∞1n\sum\limits_{n=1}^{\infty} \frac{1}{n}n=1∑∞n1发散
② 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛
- 若un>=0u_n >= 0un>=0,∑n=1∞un2\sum\limits_{n=1}^{\infty} u_n^2n=1∑∞un2收敛(limn→∞un=0\lim\limits_{n \to \infty} u_n = 0n→∞limun=0,从某项起,un<1u_n < 1un<1,un2<unu_n^2 < u_nun2<un),
- 若unu_nun 任意,则∑n=1∞un2\sum\limits_{n=1}^{\infty} u_n^2n=1∑∞un2不定(例如∑n=1∞(−1)n1n\sum\limits_{n=1}^{\infty} (-1)^n \frac{1}{\sqrt{n}}n=1∑∞(−1)nn1收敛,但∑n=1∞1n\sum\limits_{n=1}^{\infty} \frac{1}{n}n=1∑∞n1发散)。
③ 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛
- 若un>=0u_n >= 0un>=0,则∑n=1∞unun+1\sum\limits_{n=1}^{\infty} u_n u_{n+1}n=1∑∞unun+1收敛(unun+1⩽un2+un+122)\left(u_n u_{n+1} \leqslant \dfrac{u_n^2 + u_{n+1}^2}{2}\right)(unun+1⩽2un2+un+12)
- 若unu_nun任意,∑n=1∞unun+1\sum\limits_{n=1}^{\infty} u_n u_{n+1}n=1∑∞unun+1不定(例如un=(−1)n1nu_n = (-1)^n \dfrac{1}{\sqrt{n}}un=(−1)nn1,unun+1=(−1)n1n(−1)n+11n+1=−1n(n+1)\quad u_n u_{n+1} = (-1)^n \dfrac{1}{\sqrt{n}} (-1)^{n+1} \dfrac{1}{\sqrt{n+1}} = -\dfrac{1}{\sqrt{n(n+1)}}unun+1=(−1)nn1(−1)n+1n+11=−n(n+1)1,\quad级数发散).
④ 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞(−1)nun\sum\limits_{n=1}^{\infty} (-1)^n u_nn=1∑∞(−1)nun不定
- 例如∑n=1∞(−1)n1n\sum\limits_{n=1}^{\infty} (-1)^n \dfrac{1}{n}n=1∑∞(−1)nn1收敛,但∑n=1∞1n\sum\limits_{n=1}^{\infty} \dfrac{1}{n}n=1∑∞n1发散
⑤ 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞(−1)nunn\sum\limits_{n=1}^{\infty} (-1)^n \dfrac{u_n}{n}n=1∑∞(−1)nnun不定
- 例如∑n=2∞(−1)n1lnn\sum\limits_{n=2}^{\infty} (-1)^n \dfrac{1}{\ln n}n=2∑∞(−1)nlnn1收敛,但∑n=2∞1nlnn\sum\limits_{n=2}^{\infty} \dfrac{1}{n \ln n}n=2∑∞nlnn1发散
⑥ 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛
- 若un>=0u_n >= 0un>=0,则∑n=1∞u2n\sum\limits_{n=1}^{\infty} u_{2n}n=1∑∞u2n,∑n=1∞u2n−1\sum\limits_{n=1}^{\infty} u_{2n-1}n=1∑∞u2n−1均收敛
- unu_nun任意时,∑n=1∞u2n\sum\limits_{n=1}^{\infty} u_{2n}n=1∑∞u2n,∑n=1∞u2n−1\sum\limits_{n=1}^{\infty} u_{2n-1}n=1∑∞u2n−1不定
- 例如1−12+13−14+15−16+⋯=∑n=1∞(−1)n−11n1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{5} - \dfrac{1}{6} + \cdots = \sum\limits_{n=1}^{\infty} (-1)^{n-1} \dfrac{1}{n}1−21+31−41+51−61+⋯=n=1∑∞(−1)n−1n1收敛,但是其奇数项和与偶数项和都发散
⑦ 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞(u2n−1+u2n)\sum\limits_{n=1}^{\infty} (u_{2n-1} + u_{2n})n=1∑∞(u2n−1+u2n)收敛.
- 收敛级数任意加括号所得的新级数仍收敛,且和不变,但反过来推要增加limn→∞un=0\lim\limits_{n \to \infty} u_n = 0n→∞limun=0的条件
- 即只有∑n=1∞(u2n−1+u2n)\sum\limits_{n=1}^{\infty} (u_{2n-1} + u_{2n})n=1∑∞(u2n−1+u2n)收敛且limn→∞un=0\lim\limits_{n \to \infty} u_n = 0n→∞limun=0,才能推出∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛. 因S2n=(u1+u2)+(u3+u4)+⋯+(u2n−1+u2n)S_{2n} = (u_1 + u_2) + (u_3 + u_4) + \cdots + (u_{2n-1} + u_{2n})S2n=(u1+u2)+(u3+u4)+⋯+(u2n−1+u2n),limn→∞S2n=S\lim\limits_{n \to \infty} S_{2n} = Sn→∞limS2n=S存在,S2n+1=S2n+u2n+1S_{2n+1} = S_{2n} + u_{2n+1}S2n+1=S2n+u2n+1,limn→∞S2n+1=S+limn→∞u2n+1=S\lim\limits_{n \to \infty} S_{2n+1} = S + \lim\limits_{n \to \infty} u_{2n+1} = Sn→∞limS2n+1=S+n→∞limu2n+1=S,即可得∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛.)
⑧ 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则∑n=1∞(u2n−1−u2n)\sum\limits_{n=1}^{\infty} (u_{2n-1} - u_{2n})n=1∑∞(u2n−1−u2n)不定.
- 例如u1+u2+u3+u4+u5+u6+⋯=1−12+13−14+15−16+⋯u_1 + u_2 + u_3 + u_4 + u_5 + u_6 + \cdots = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{5} - \dfrac{1}{6} + \cdotsu1+u2+u3+u4+u5+u6+⋯=1−21+31−41+51−61+⋯收敛
- 但(1+12)+(13+14)+(15+16)+⋯\left(1 + \dfrac{1}{2}\right) + \left(\dfrac{1}{3} + \dfrac{1}{4}\right) + \left(\dfrac{1}{5} + \dfrac{1}{6}\right) + \cdots(1+21)+(31+41)+(51+61)+⋯发散
⑨ 设∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,则
- ∑n=1∞(un+un+1)\sum\limits_{n=1}^{\infty} (u_n + u_{n+1})n=1∑∞(un+un+1)收敛,∑n=1∞un+∑n=1∞un+1\sum\limits_{n=1}^{\infty} u_n + \sum\limits_{n=1}^{\infty} u_{n+1}n=1∑∞un+n=1∑∞un+1收敛,
- ∑n=1∞(un−un+1)\sum\limits_{n=1}^{\infty} (u_n - u_{n+1})n=1∑∞(un−un+1)收敛,∑n=1∞un−∑n=1∞un+1\sum\limits_{n=1}^{\infty} u_n - \sum\limits_{n=1}^{\infty} u_{n+1}n=1∑∞un−n=1∑∞un+1收敛.
⑩ 若∑n=1∞∣un∣\sum\limits_{n=1}^{\infty} |u_n|n=1∑∞∣un∣收敛,则∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛;若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un发散,则∑n=1∞∣un∣\sum\limits_{n=1}^{\infty} |u_n|n=1∑∞∣un∣发散.
⑪ 若∑n=1∞un2\sum\limits_{n=1}^{\infty} u_n^2n=1∑∞un2收敛,则∑n=1∞unn\sum\limits_{n=1}^{\infty} \dfrac{u_n}{n}n=1∑∞nun绝对收敛
- 证明思路:(∣unn∣⩽12(un2+1n2))\left(\left|\dfrac{u_n}{n}\right| \leqslant \dfrac{1}{2}\left(u_n^2 + \dfrac{1}{n^2}\right)\right)(nun⩽21(un2+n21)).
⑫ 设a,b,ca,b,ca,b,c为非零常数,且aun+bvn+cwn=0au_n + bv_n + cw_n = 0aun+bvn+cwn=0,则在∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un,∑n=1∞vn\sum\limits_{n=1}^{\infty} v_nn=1∑∞vn和∑n=1∞wn\sum\limits_{n=1}^{\infty} w_nn=1∑∞wn中只要有两个级数是收敛的,另一个必收敛.
⑬ 若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,∑n=1∞vn\sum\limits_{n=1}^{\infty} v_nn=1∑∞vn收敛,则∑n=1∞(un±vn)\sum\limits_{n=1}^{\infty} (u_n \pm v_n)n=1∑∞(un±vn)收敛.
⑭ 若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,∑n=1∞vn\sum\limits_{n=1}^{\infty} v_nn=1∑∞vn发散,则∑n=1∞(un±vn)\sum\limits_{n=1}^{\infty} (u_n \pm v_n)n=1∑∞(un±vn)发散.
⑮ 已知∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un发散,∑n=1∞vn\sum\limits_{n=1}^{\infty} v_nn=1∑∞vn发散
-
若un⩾0,vn⩾0u_n \geqslant 0, v_n \geqslant 0un⩾0,vn⩾0,则∑n=1∞(un+vn)\sum\limits_{n=1}^{\infty} (u_n + v_n)n=1∑∞(un+vn)发散
-
若un,vnu_n, v_nun,vn任意,∑n=1∞(un±vn)\sum\limits_{n=1}^{\infty} (u_n \pm v_n)n=1∑∞(un±vn)不定.(见⑥)
⑯ 若∑n=1∞un\sum\limits_{n=1}^{\infty} u_nn=1∑∞un收敛,∑n=1∞vn\sum\limits_{n=1}^{\infty} v_nn=1∑∞vn收敛
- 当un⩾0,vn⩾0u_n \geqslant 0, v_n \geqslant 0un⩾0,vn⩾0时,∑n=1∞unvn\sum\limits_{n=1}^{\infty} u_n v_nn=1∑∞unvn收敛(unvn⩽un2+vn22)\left(u_n v_n \leqslant \dfrac{u_n^2 + v_n^2}{2}\right)(unvn⩽2un2+vn2)
- 若unu_nun任意,vn⩾0v_n \geqslant 0vn⩾0时,∑n=1∞∣un∣⋅vn\sum\limits_{n=1}^{\infty} |u_n| \cdot v_nn=1∑∞∣un∣⋅vn收敛(limn→∞∣un∣⋅vnvn=limn→∞∣un∣=0)\left(\lim\limits_{n \to \infty} \dfrac{|u_n| \cdot v_n}{v_n} = \lim\limits_{n \to \infty} |u_n| = 0\right)(n→∞limvn∣un∣⋅vn=n→∞lim∣un∣=0)
- 若unu_nun任意,vnv_nvn任意,∑n=1∞unvn\sum\limits_{n=1}^{\infty} u_n v_nn=1∑∞unvn不定.
级数收敛的性质
- 级数收敛的本质,就是前n项和的极限存在(部分和数列极限存在)
- 级数收敛,其通项极限必然趋于0
- 多个收敛级数的线性组合依然收敛
- 一个收敛的级数去掉或者添加有限项,该级数依然收敛
- 收敛级数的和具有唯一性
部分项级数的敛散性
对一个正项级数来说,如果它本身是收敛的,请问它的偶数项级数是否收敛?
没错,这其实涉及到正项级数的一个基本性质:若正项级数 ∑vn\sum v_n∑vn 收敛,则其任意部分项构成的正项级数 ∑vnk\sum v_{n_k}∑vnk 也收敛
下面我们就来尝试理解一下这个性质:我们知道,级数与它对应的部分和数列之间有着千丝万缕的联系。比如级数收敛,就等价于部分和数列的极限存在。那么要证明偶数项级数收敛,其实就可以转化成证明对应的部分和数列极限存在。而证明数列极限存在最常用的方法就是单调有界准则。下面我们就用单调有界准则,来证明上面那个基本性质
- 设原正项级数前 nnn 项和为 SnS_nSn,由原级数收敛,可以得到数列{Sn}\{S_n\}{Sn}有上界。设 sup{Sn}=S\sup\{S_n\} = Ssup{Sn}=S(SSS 为有限常数)
- 设偶数项级数前 kkk 项和为 Tk=u2+u4+⋯+u2kT_k = u_2 + u_4 + \cdots + u_{2k}Tk=u2+u4+⋯+u2k,由于原级数是正项级数,所以其偶数项级数依然是正项级数(每一项都是正数),则数列{Tk}\{T_k\}{Tk}肯定是单调递增的
- 由于 un>0u_n > 0un>0,有 Tk=u2+u4+⋯+u2k<u1+u2+u3+⋯+u2k=S2k≤ST_k = u_2 + u_4 + \cdots + u_{2k} < u_1 + u_2 + u_3 + \cdots + u_{2k} = S_{2k} \leq STk=u2+u4+⋯+u2k<u1+u2+u3+⋯+u2k=S2k≤S,即数列{Tk}\{T_k\}{Tk} 有上界。
- 因此 limk→∞Tk\lim_{k \to \infty} T_klimk→∞Tk 存在,即偶数项级数收敛。
紧接着我们也可以把这个结论推广到原正项级数的任意子级数,由于正项级数每一项都是正的,因此其所有子级数的前n项和数列{Tn}\{T_n\}{Tn}都是单调递增的,又因为其是原正项级数的子级数,所以其少了某些项的部分和肯定不会超过原正项级数的对应前n项和。原正项级数的对应前n项和都有上界(因为原正项级数收敛),所以子级数的部分和数列肯定也有上界,最后根据单调有界准则,我们可以说明正项级数的任意子集构成的级数也是收敛的
对一个幂级数来说,请问在它的收敛域内,其对应的偶数项级数是否收敛?
对于幂级数而言,若原幂级数在其收敛域内的某点收敛,则该点处的偶数项幂级数一定收敛
首先我们要明确幂级数与偶数项幂级数的定义
- 原幂级数:标准形式为 ∑n=0∞anxn=a0+a1x+a2x2+a3x3+⋯+anxn+…\sum_{n=0}^{\infty} a_n x^n = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \dots + a_n x^n + \dots∑n=0∞anxn=a0+a1x+a2x2+a3x3+⋯+anxn+…,其中 ana_nan 为系数,xxx 为变量。其收敛域是所有使级数收敛的 xxx 的集合,具有“对称区间性”(除端点外,收敛域为 (−R,R)(-R, R)(−R,R),RRR 为收敛半径)。
- 偶数项幂级数:取原幂级数中序号 nnn 为偶数的项构成,形式为 ∑k=0∞a2kx2k=a0+a2x2+a4x4+⋯+a2kx2k+…\sum_{k=0}^{\infty} a_{2k} x^{2k} = a_0 + a_2 x^2 + a_4 x^4 + \dots + a_{2k} x^{2k} + \dots∑k=0∞a2kx2k=a0+a2x2+a4x4+⋯+a2kx2k+…(本质是“以 t=x2t = x^2t=x2 为变量的幂级数” ∑k=0∞a2ktk\sum_{k=0}^{\infty} a_{2k} t^k∑k=0∞a2ktk)。
由于幂级数在收敛域内的收敛性(除端点外)是“绝对收敛”(可由比值判别法验证),即 ∑n=0∞∣anx0n∣\sum_{n=0}^{\infty} |a_n x_0^n|∑n=0∞∣anx0n∣ 收敛。而偶数项幂级数的绝对值级数 ∑k=0∞∣a2kx02k∣\sum_{k=0}^{\infty} |a_{2k} x_0^{2k}|∑k=0∞∣a2kx02k∣ 是 ∑n=0∞∣anx0n∣\sum_{n=0}^{\infty} |a_n x_0^n|∑n=0∞∣anx0n∣ 的部分项级数(仅保留偶数项)。
根据正项级数的基本性质:若正项级数 ∑vn\sum v_n∑vn 收敛,则其任意部分项构成的正项级数 ∑vnk\sum v_{n_k}∑vnk 也收敛(因为部分项级数的部分和是原级数部分和的“子列”,而收敛的单调递增数列(正项级数部分和)的子列仍收敛)。
由于 ∑n=0∞∣anx0n∣\sum_{n=0}^{\infty} |a_n x_0^n|∑n=0∞∣anx0n∣ 是收敛的正项级数,因此其部分项级数 ∑k=0∞∣a2kx02k∣\sum_{k=0}^{\infty} |a_{2k} x_0^{2k}|∑k=0∞∣a2kx02k∣ 收敛,进而推出 偶数项幂级数 ∑k=0∞a2kx02k\sum_{k=0}^{\infty} a_{2k} x_0^{2k}∑k=0∞a2kx02k 绝对收敛,故收敛。
延伸:偶数项幂级数的收敛域与原级数的关系
其实收敛半径没变

幂级数
什么是函数项级数?
前面我们讨论的级数都是数项级数,它的一个最大的特点就是:其敛散性
是确定的,要么收敛,要么发散。而我们下面要讲的函数项级数就不一样了,它的敛散性是不确定的,会随着自变量x的变化而变化。
我们知道,当x的值确定时,函数项级数就退化成了一个数项级数,很有可能x取这个值时,对应的数项级数就收敛了,而x取另一个值时,对应的数项级数又发散了。因此我们研究函数项级数的一个重要的课题,就是要研究这个函数项级数在x取那些值时是收敛的,在x取哪些值时是发散的。我们在学术上面,就把上面这个问题叫做求函数项级数的收敛域
幂级数的定义
幂级数是一类特殊的函数项级数,其一般形式是以“幂函数”为通项的无穷级数,核心是将函数表示为无穷多个幂函数的和,形式如下:
1. 标准形式(以 x=ax = ax=a 为中心的幂级数)
形如
∑n=0∞an(x−a)n=a0+a1(x−a)+a2(x−a)2+⋯+an(x−a)n+⋯\sum_{n=0}^{\infty} a_n (x - a)^n = a_0 + a_1 (x - a) + a_2 (x - a)^2 + \cdots + a_n (x - a)^n + \cdots∑n=0∞an(x−a)n=a0+a1(x−a)+a2(x−a)2+⋯+an(x−a)n+⋯
的级数称为以 aaa 为中心(或展开点)的幂级数,其中 ana_nan(n=0,1,2,…n = 0, 1, 2, \dotsn=0,1,2,…)是幂级数的系数,aaa 是常数,xxx 是变量。
2. 特殊形式:以 x=0x = 0x=0 为中心的幂级数,也叫“麦克劳林级数”形式
当 a=0a = 0a=0 时,幂级数简化为
∑n=0∞anxn=a0+a1x+a2x2+⋯+anxn+⋯\sum_{n=0}^{\infty} a_n x^n = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n + \cdots∑n=0∞anxn=a0+a1x+a2x2+⋯+anxn+⋯
这是最常见的幂级数形式,许多基本函数(如 ex,sinx,cosxe^x, \sin x, \cos xex,sinx,cosx 等)的幂级数展开都以此为基础。
3. 核心本质
幂级数的本质是用无穷多个幂函数的线性组合来逼近一个函数,其收敛性具有“区间特性”(存在收敛区间和收敛半径),这是它区别于数项级数的关键——数项级数是“常数项的和”,而幂级数是“函数项的和”,其敛散性与变量 xxx 的取值密切相关。
例如,指数函数 exe^xex 的幂级数展开(麦克劳林级数)为:
ex=∑n=0∞xnn!=1+x+x22!+x33!+⋯(x∈R)e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \quad (x \in \mathbb{R})ex=∑n=0∞n!xn=1+x+2!x2+3!x3+⋯(x∈R)
这里每一项都是 xxx 的幂函数,通过无穷求和精确表示了 exe^xex。
常见幂级数

幂级数的收敛域介绍(阿贝尔定理)
前面我们说了,研究一个函数项级数,非常重要的一个课题就是研究它的收敛域。幂级数作为一个典型的函数项级数,当然也不例外。那到底自变量x取哪些值,能让幂级数收敛呢?
科学家阿贝尔通过研究告诉我们,对于∑n=0∞an(x−a)n\sum_{n=0}^{\infty} a_n (x - a)^n∑n=0∞an(x−a)n这样的一个幂级数,它会以 x=ax=ax=a 为中心,存在一个收敛半径RRR。
-
当 x∈(a−R,a+R),即∣x−a∣<Rx \in (a-R, a+R),即|x-a| <Rx∈(a−R,a+R),即∣x−a∣<R 时,幂级数∑n=0∞an(x−a)n\sum_{n=0}^{\infty} a_n (x - a)^n∑n=0∞an(x−a)n就是收敛的。
-
而当 x∈(−∞,a−R)∪(a+R,+∞),即∣x−a∣<Rx \in (-\infty, a-R) \cup (a+R, +\infty),即|x-a| <Rx∈(−∞,a−R)∪(a+R,+∞),即∣x−a∣<R 时,幂级数∑n=0∞an(x−a)n\sum_{n=0}^{\infty} a_n (x - a)^n∑n=0∞an(x−a)n肯定是发散的
-
当 x=a−Rx = a-Rx=a−R 或 a+Ra+Ra+R 时,其带入之后对应数项级数的敛散性是不确定的,我们要通过前面说过的数项级数判敛的方法,来具体确定
求幂级数的收敛半径
说到这里大家肯定有个疑问:你前面这么一说,我大概知道幂级数的收敛域是啥了,但你没告诉我一个很关键的东西,那就是——幂级数的收敛半径RRR是咋求的啊?
1. 比值判别法(达朗贝尔判别法)
若幂级数系数 an≠0a_n \neq 0an=0,且 limn→∞∣an+1an∣=L\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = Llimn→∞anan+1=L(LLL 为非负实数或 +∞+\infty+∞),则收敛半径 RRR 为:
- 当 0<L<+∞0 < L < +\infty0<L<+∞ 时,R=1LR = \frac{1}{L}R=L1;
- 当 L=0L = 0L=0 时,R=+∞R = +\inftyR=+∞(全数轴收敛);
- 当 L=+∞L = +\inftyL=+∞ 时,R=0R = 0R=0(仅在 x=x0x = x_0x=x0 处收敛)。
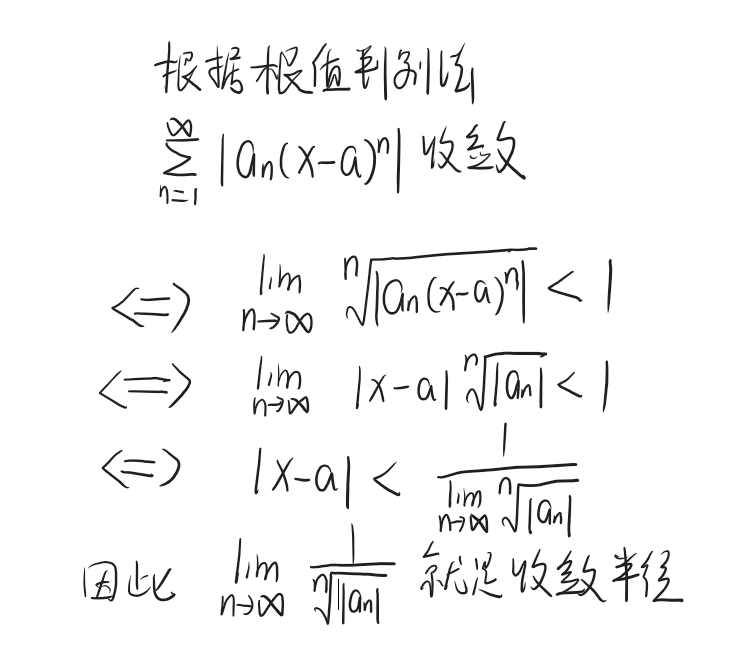
2. 根值判别法(柯西判别法)
若 limn→∞∣an∣n=ρ\lim_{n \to \infty} \sqrt[n]{|a_n|} = \rholimn→∞n∣an∣=ρ(ρ\rhoρ 为非负实数或 +∞+\infty+∞),则收敛半径 RRR 为:
- 当 0<ρ<+∞0 < \rho < +\infty0<ρ<+∞ 时,R=1ρR = \frac{1}{\rho}R=ρ1;
- 当 ρ=0\rho = 0ρ=0 时,R=+∞R = +\inftyR=+∞;
- 当 ρ=+∞\rho = +\inftyρ=+∞ 时,R=0R = 0R=0。
看完之后是不是觉得非常似曾相识?没错!我们刚刚在正项级数的判敛法中也学过这两种方法!其实上面两种求收敛半径的方法,就是由对应的正项级数判敛法推过来的!下面我就给你简单推一下
在具体推之前,我们还要做一些铺垫工作。前面我们提到,科学家阿贝尔告诉我们,幂级数的收敛域特征非常明显,那就是会以x=ax=ax=a为圆心,某个正数RRR为收敛半径,画一个圈(a−R,a+R)(a-R, a+R)(a−R,a+R),x取这个圈里面的值,对应的数项级数一定是绝对收敛的。x取落在这个圈外的值,对应的数项级数一定是发散的。x取这个圈边缘上的值,对应的数项级数可能发散,可能条件收敛,也可能绝对收敛
这其实有两个非常值得我们注意的点
- 第一个就是,x取收敛域圈里面的值,对应的级数不仅收敛,而且是绝对收敛(即给通项加了绝对值之后,级数仍然收敛)
- 第二个就是,当且仅当x取收敛域边缘的数,对应的数项级数才可能条件收敛(也就是说,如果一个题目告诉你,在幂函数中x取某某值,对应的数项级数条件收敛,你立即就可以确定,这个值就是收敛域的一个端点)
好了,知道这个之后,我们就可以来推导幂级数的收敛半径计算公式了
当xxx取了具体值之后,∑n=1∞an(x−a)n\sum_{n=1}^{\infty} a_n (x - a)^n∑n=1∞an(x−a)n就变成了数项级数
根据阿贝尔定理,若xxx在收敛域内,其对应的数项级数不仅收敛,而且是绝对收敛
即 当xxx在收敛域内时,∑n=1∞an(x−a)n\sum_{n=1}^{\infty} a_n (x - a)^n∑n=1∞an(x−a)n绝对收敛
即 当xxx在收敛域内时,∑n=1∞∣an(x−a)n∣\sum_{n=1}^{\infty} |a_n (x - a)^n|∑n=1∞∣an(x−a)n∣收敛

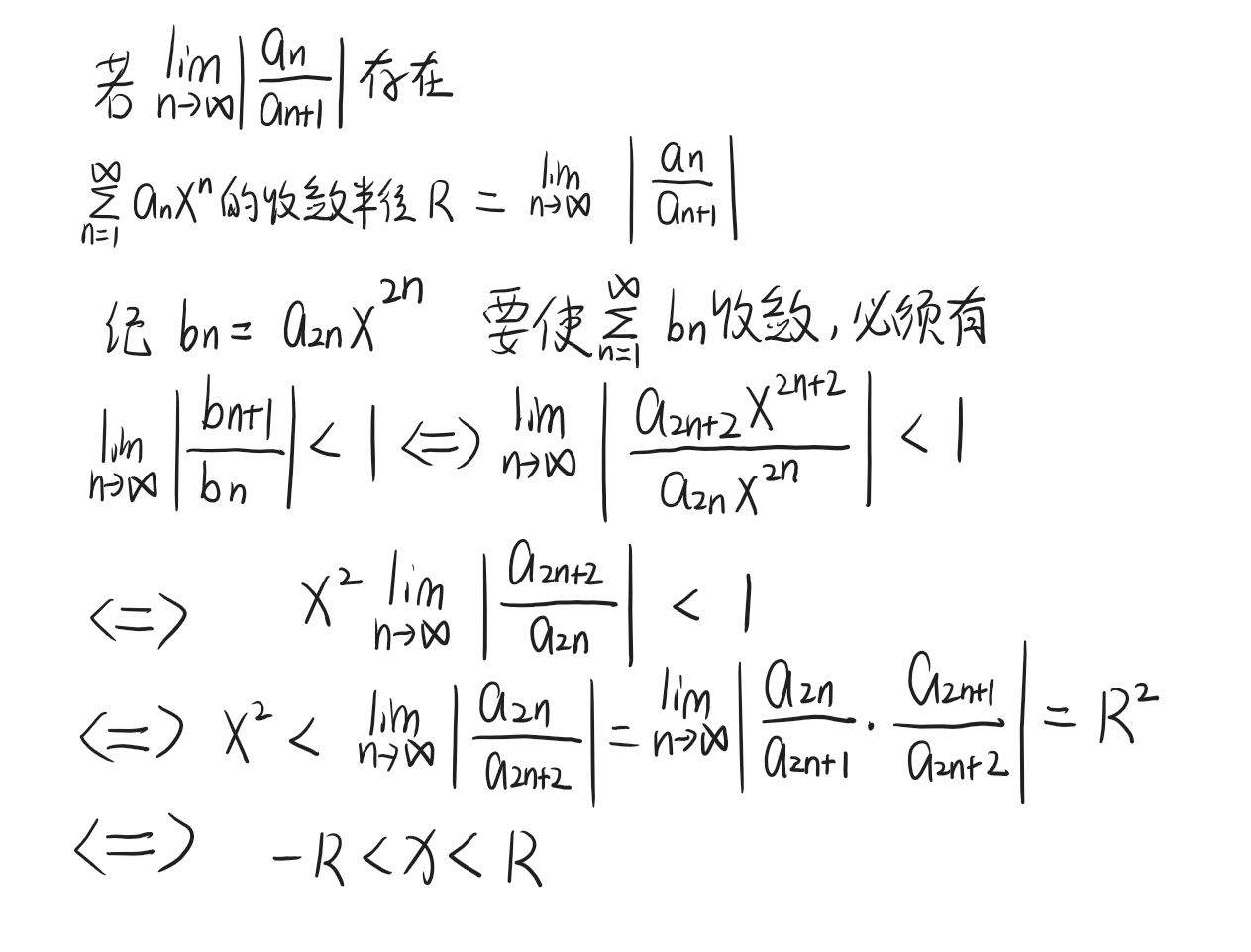
根据上面的思路,我们也可以得出缺少某些项的幂函数的收敛半径的计算方法
3. 缺项幂级数的特殊处理
若幂级数缺少某些次数的项(如 ∑n=0∞anx2n\sum_{n=0}^{\infty} a_n x^{2n}∑n=0∞anx2n 或 ∑n=0∞anx2n+1\sum_{n=0}^{\infty} a_n x^{2n+1}∑n=0∞anx2n+1),需将其视为函数项级数,直接对通项 un(x)u_n(x)un(x) 用比值或根值判别法(对 xxx 求极限)。
例:求 ∑n=1∞x2nn⋅4n\sum_{n=1}^{\infty} \frac{x^{2n}}{n \cdot 4^n}∑n=1∞n⋅4nx2n 的收敛半径。
令 un(x)=x2nn⋅4nu_n(x) = \frac{x^{2n}}{n \cdot 4^n}un(x)=n⋅4nx2n,用根值判别法:
limn→∞∣un(x)∣n=limn→∞x24=x24\lim_{n \to \infty} \sqrt[n]{|u_n(x)|} = \lim_{n \to \infty} \frac{x^2}{4} = \frac{x^2}{4}n→∞limn∣un(x)∣=n→∞lim4x2=4x2
令 x24<1\frac{x^2}{4} < 14x2<1,得 ∣x∣<2|x| < 2∣x∣<2,故收敛半径 R=2R = 2R=2。
傅里叶级数
傅里叶级数的引入
这个我觉得教材就写的贼好,直接看教材


傅里叶级数的定义
狄利克雷条件:一个周期函数在其周期内连续,或有限个第一类间断点、有限个极值点、绝对可积
傅里叶变换的核心是:对于任意一个周期函数,只要它满足狄利克雷条件,我们都可以通过傅里叶变换,将其分解为一个傅里叶级数
傅里叶级数的实函数形式
下面我们给出了傅里叶级数最常用的形式,由常数项、余弦项和正弦项组成:
f(t)=a02+∑n=1∞[ancos(nω0t)+bnsin(nω0t)]f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left[ a_n\cos(n\omega_0 t) + b_n\sin(n\omega_0 t) \right]f(t)=2a0+∑n=1∞[ancos(nω0t)+bnsin(nω0t)]
- a02\frac{a_0}{2}2a0:直流分量(常数项),是函数在一个周期内的平均值。
- nω0n\omega_0nω0:n次谐波的角频率(n为正整数,n=1时为基波,n≥2时为高次谐波)。
- an、bna_n、b_nan、bn:傅里叶系数,决定各次谐波的振幅。
傅里叶级数还有一种复函数表示形式,但是不咋考,所以我们就不说了
下面我们给出上述定义中an、bna_n、b_nan、bn的求法


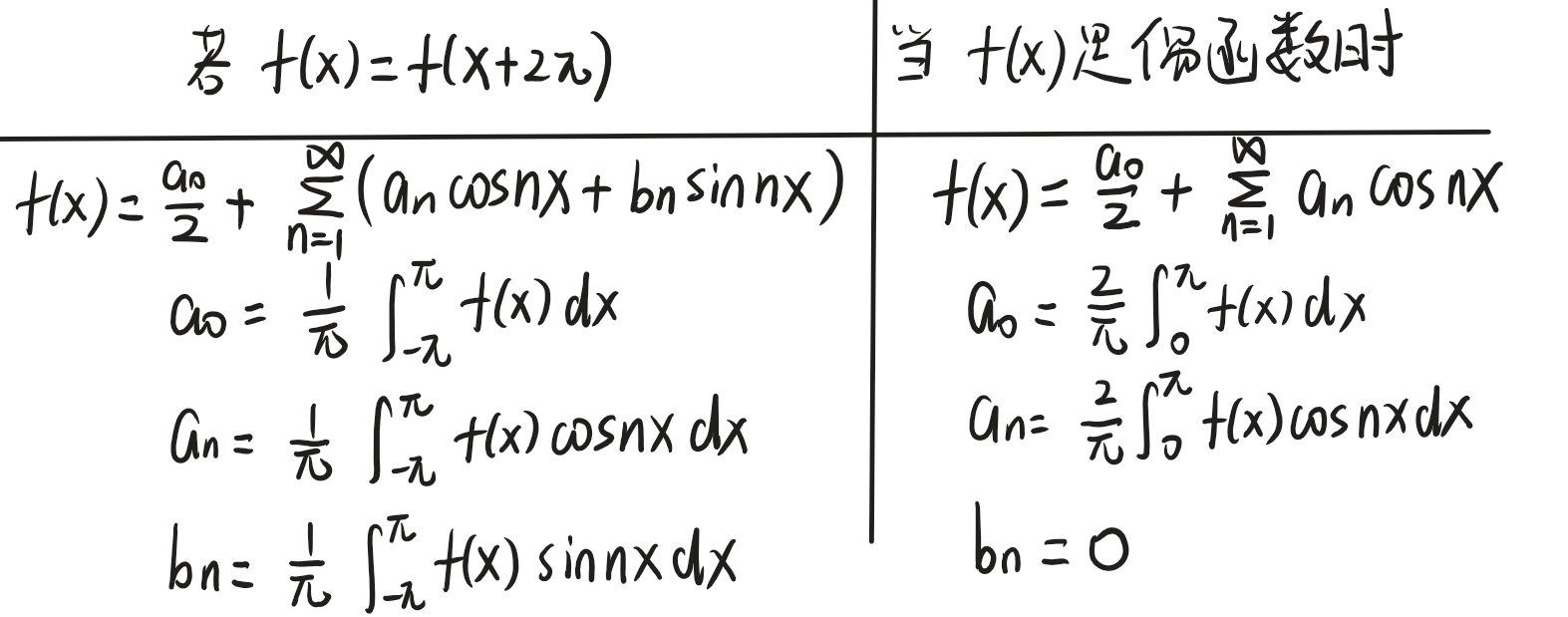
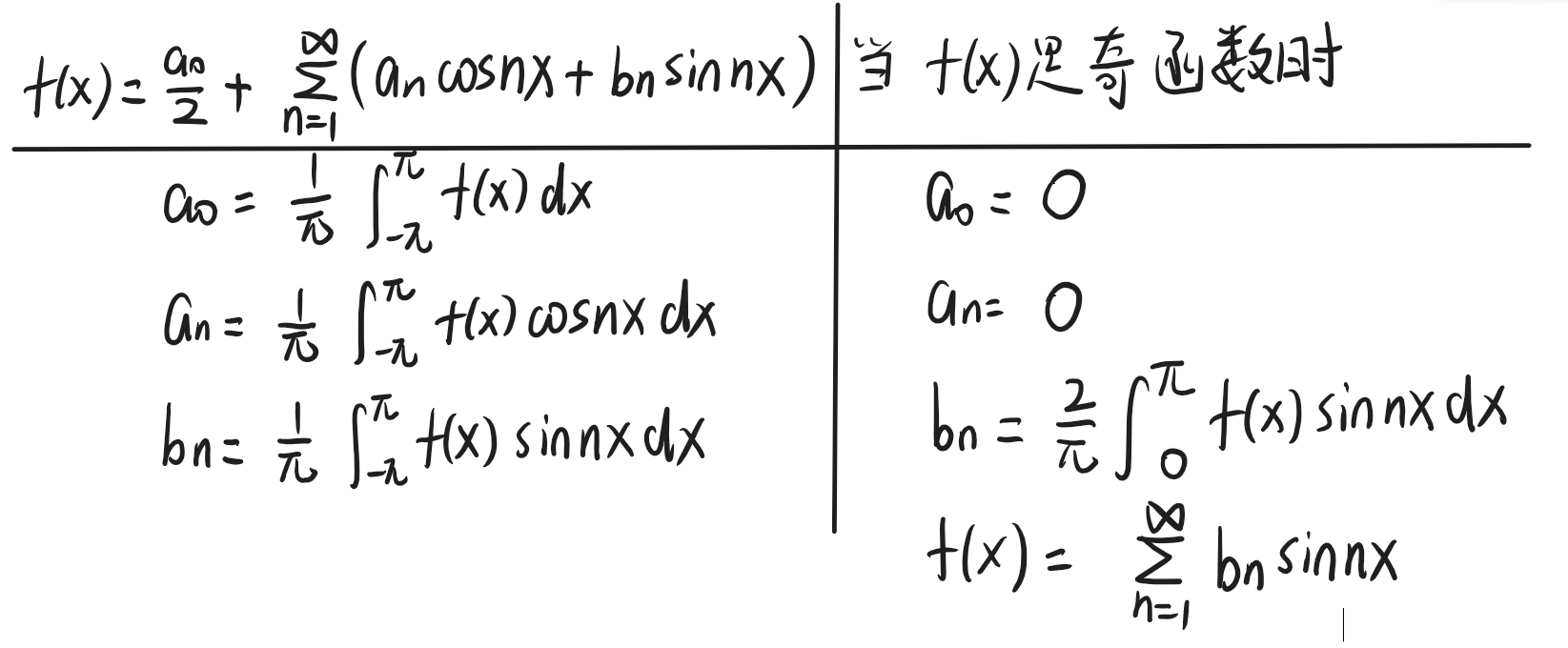
狄利克雷收敛定理
设f(x)f(x)f(x)是周期为2l2l2l的周期函数,如果它满足狄利克雷条件,即:
- 在一个周期内连续或只有有限个第一类间断点
- 在一个周期内至多只有有限个极值点
那么f(x)f(x)f(x)的傅里叶级数收敛,并且
- 当xxx是f(x)f(x)f(x)的连续点时,级数收敛于f(x)f(x)f(x);
- 当xxx是f(x)f(x)f(x)的间断点时,级数收敛于12[f(x−)+f(x+)]\frac{1}{2}[f(x^-) + f(x^+)]21[f(x−)+f(x+)]
经典例题
求∑n=1∞1n2\sum_{n=1}^{\infty} \frac{1}{n^2}∑n=1∞n21
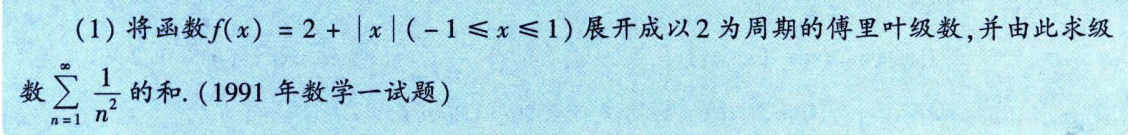
答案:∑n=1∞1n2=π26\sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}∑n=1∞n21=6π2

求∑n=1∞(−1)n−1n2\sum_{n = 1}^{\infty} \frac{(-1)^{n - 1}}{n^2}∑n=1∞n2(−1)n−1






















 4220
4220

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








