Mod Tree(扩展BSGS)

最新推荐文章于 2021-08-19 23:56:06 发布

原创最新推荐文章于 2021-08-19 23:56:06 发布 · 341 阅读

1 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

128 篇文章

订阅专栏

本文探讨了一种算法问题——给定一棵每个节点有K个孩子的树，寻找最小的层数D，使得该层的节点数量模P等于N。文章通过扩展BSGS算法解决了这一问题，并提供了完整的AC代码。

Mod Tree

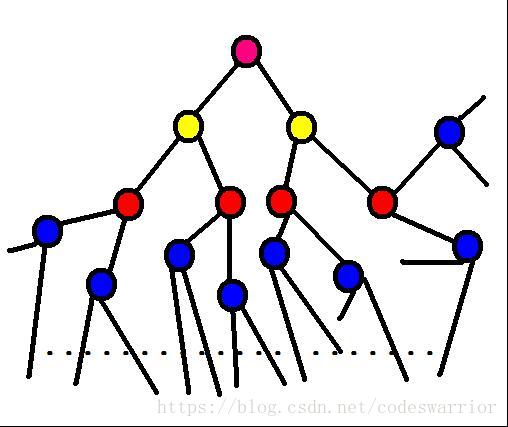
这里写图片描述

 The picture indicates a tree, every node has 2 children.
  The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
  Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.

Input
The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)
Output
The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”
Sample Input

3 78992 453
4 1314520 65536
5 1234 67

Sample Output

Orz,I can’t find D!
8
20

题意：

给定每个节点的孩子数K求最小层数使得该层的节点数模P等于N

分析：

即求

K x \equiv N (m o d P)

$K^x \equiv N\ (mod \ P)$

因为P不一定是素数故需要用扩展BSGS

很奇怪的是做了好几道BSGS的题目了，抄模板一直wa，在抄一遍又过了，都不知道哪里错的

ACcode：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll q_pow(ll a, ll b, ll mod){
    ll ans = 1;
    while(b){
        if(b & 1) ans = ans * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return ans;
}

ll gcd(ll a,ll b){
    return b ? gcd(b,a%b) : a;
}

void ex_gcd(ll a,ll b,ll &x,ll &y){
    if(!b){
        x = 1;
        y = 0;
        return;
    }
    ex_gcd(b,a%b,y,x);
    y -= a / b * x;
    return;
}

ll BSGS(ll a,ll b,ll p){
    a %= p;
    b %= p;
    ll ret = 1;
    for(ll i = 0; i <= 50; i++){
        if(ret == b) return i;
        ret = ret * a % p;
    }
    ll x,y,d,v = 1,cnt = 0;
    while((d = gcd(a,p)) != 1){
        if(b % d) return -1;
        b /= d;
        p /= d;
        v = v * (a / d) % p;
        cnt++;
    }
    map<ll,ll>h;
    ll m = ceil(sqrt(p)),t = 1;
    for(ll i = 0; i < m; i++){
        if(h.count(t)) h[t] = min(h[t],i);
        else h[t] = i;
        t = t * a % p;
    }
    for(ll i = 0; i < m; i++){
        ex_gcd(v,p,x,y);
        x = (x * b % p + p) % p;
        if(h.count(x)) return i * m + h[x] + cnt;
        v = v * t % p;
    }
    return -1;
}

int main(){
    ll k,p,n;
    while(~scanf("%lld%lld%lld",&k,&p,&n)){
        if(n >= p){
            puts("Orz,I can’t find D!");
            continue;
        }
        ll ans = BSGS(k,n,p);
        if(ans == -1) puts("Orz,I can’t find D!");
        else printf("%lld\n",ans);
    }
    return 0;
}