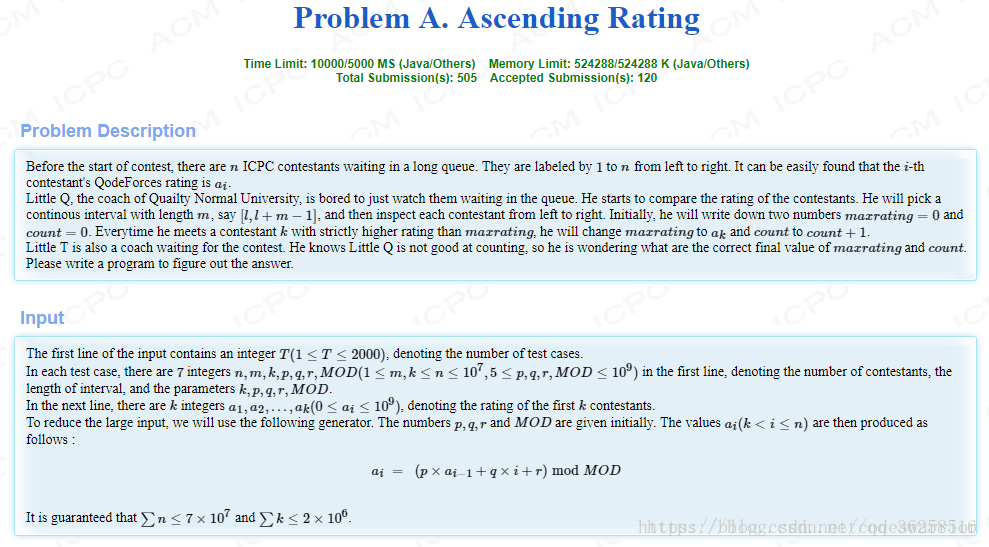
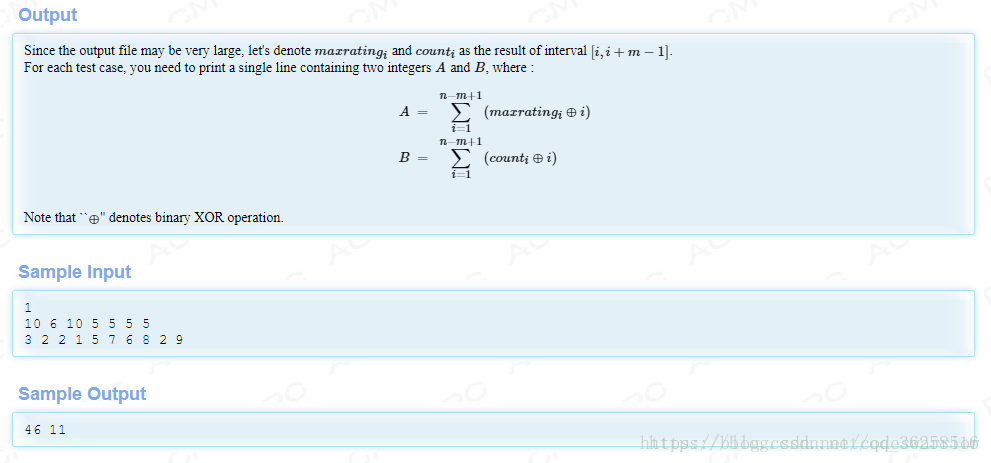
题意:
找到1-n中间每个间隔为m的最大值,和获得这个最大值的比较次数,然后按照题目所给公式将每个区间的结果异或i得到最终结果
分析:
首先观察数据我们知道,一定不能跑二次循环,即每个枚举每个区间,然后在每个区间中再遍历比较最大值并记录次数,这样的复杂度是O(mn)的必然超时,因此我们得想到用O(n)的方法来解决这个问题
那么就是单调队列
我们可以从前往后遍历维护一个单调递减队列,队列中存标号,这样我们就可以得每个区间的最大值
例如3 5 7 9
首先3入队
{3}
然后到5,先将3出队,再将5入队
{5}
然后到7,先将5出队,再将7入队
{7}
最后同理7出队,9入队
{9}
所以最大值是9,即队列的最左端元素是最大的
怎么保证这个最左端元素一定在m的间距范围呢
只需要保证最左端的元素下标,应当大于等于i-m+1,如果小于说明在i区间的左侧,就出队,这样也就是记录了第i个区间的最大值了。
但是我们发现按照这种方式,我们只能得到最大值却不能得到次数
这样因为我们希望较大的值进去后就不在出来了,这样就可以记录下区间内最大值的替换过程
只需要倒着遍历维护单调递减区间即可
还是刚才的例子我们倒着遍历其实是遍历
9 7 5 3
这样9先入队,很明显他是最大的,之后不会破坏单调性,也就不会再出来了
{9}
7入队
{9,7}
5入队
{9,7,5}
3入队
{9,7,5,3}
这样我们相当于一共换了3次,就得到了相应区间的交换次数。
code:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 7e7+10;
typedef long long ll;
int arr[maxn],maxval[maxn],que[maxn],num[maxn];
int n,m,k,p,q,r,mod;
void getMax(int n,int k){
int head = 0,rear = 0;
for(int i = 1; i <= n; i++){
while(rear > head && arr[que[rear-1]] <= arr[i]) rear--;
que[rear++] = i;
if(i < k) continue;
while(que[head] < i - k + 1) head++;
maxval[i] = arr[que[head]];
}
}
void getNum(int n,int k){
int head = 0, rear = 0;
for(int i = n; i >= 1; i--){//倒着遍历
while(rear > head && arr[que[rear-1]] <= arr[i]) rear--;
que[rear++] = i;
if(i > n - k + 1) continue;
while(que[head] > i + k - 1) head++;//这里因为是倒着遍历的,所以head++坐标会变小,不断这样下去就可以满足范围了
num[i] = rear - head;
}
}
int main(){
int t;
scanf("%d",&t);
while(t--){
scanf("%d%d%d%d%d%d%d",&n,&m,&k,&p,&q,&r,&mod);
for(int i = 1; i <= k; i++){
scanf("%d",&arr[i]);
}
for(int i = k + 1; i <= n; i++){
arr[i] = ((ll)p % mod * arr[i-1] % mod + (ll)q % mod * i % mod + r % mod) % mod;
}
getMax(n,m);
getNum(n,m);
ll b = 0, a = 0;
for(int i = 1; i <= n - m + 1; i++){
b = b + (num[i] ^ i);
a = a + (maxval[i+m-1] ^ i);
}
printf("%lld %lld\n",a,b);
}
return 0;
}




 本文介绍了一种使用单调队列求解区间最大值及比较次数的高效算法,通过正向遍历获取最大值,逆向遍历记录比较次数,避免了传统方法的高时间复杂度。
本文介绍了一种使用单调队列求解区间最大值及比较次数的高效算法,通过正向遍历获取最大值,逆向遍历记录比较次数,避免了传统方法的高时间复杂度。
















 235
235

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








