Machine Learning Notes II

Machine Learning Notes II

1.Classification

Focus on Binary classification problem

• Hypothesis representation
  using Sigmoid Function,also called logistic function
  
  The function looks like this->
  
  what needs to be emphasized is that z here is the theta’s transpose multiplies X.(Actually,this depends on the input of your X and theta, you can refer to the formula in the past when we talked about the linear regression)
• Decision Boundary
  for simple decision boundary, it may looks like this->
  
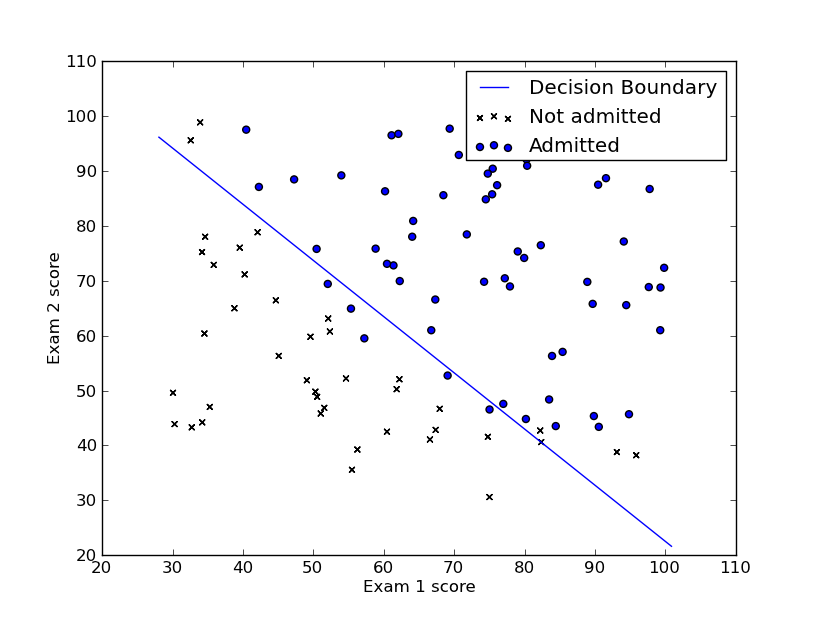
  Combine the hypothesis function with this image, we can find that:
  if z>=0, then h>=0.5 (which means it’s admitted)
  else(z<0), then h<0.5 (which means it’s not admitted)
• Cost function
  
• Gradient Descent
  The general form of gradient descent is->
  
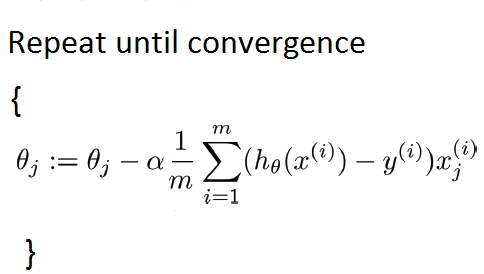
  Attention: You can find that the gradient descent here is almost the same as the way we used for linear regression. However, they are different, and the only difference is function h.

2.Multi-class Classification

Instead of y={0,1}, we’ll expend our definition so that y={0,1,..,n}.The way we solve it is dividing the problems into n+1 classificaiton problems.

3.Regulation

• The problem of overfitting && underfitting
  
  From the image above, we can see that the second pic is the right func we want.If the h is too simple or too complicated, func won’t perform well(which means the predictions are not so well).
  Underfitting, or high bias, is when the form of our hypothesis function h maps poorly to trend of the data, which is usually caused by a function that is too simple or uses too few features.
  For overfitting, or high variance,is caused by a hypothesis functionthat fits the avaliable data but doesn’t generalize well to predict data. It’s usually caused by a comlicated fucntion that creates a lot of unnecessary curves and angles unrelated to the data.
• Use regularization to solve this problem
  Keep all the features but reduce the magnitude of parameters theta.
  
  • cost function with regularization
    
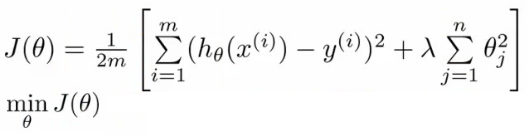
    Attention: theta here must begin from 2,and the 1 means theta 0,which isn’t regularized.
  • Gradient descent
    
  • For normal equation
    To add in regularization, the equation is the same as the orignal, except that we add another term inside the paratheses: