备战蓝桥杯---搜索（DFS基础2）

最新推荐文章于 2025-11-25 00:04:22 发布

原创最新推荐文章于 2025-11-25 00:04:22 发布 · 674 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #算法 #c++ #蓝桥杯

本文介绍了如何在二维数组中应用深度优先搜索(DFS)解决一个问题，包括对边界条件的判断，避免死循环，以及提供示例AC代码。

下面我主要介绍一下深搜的简单应用吧：

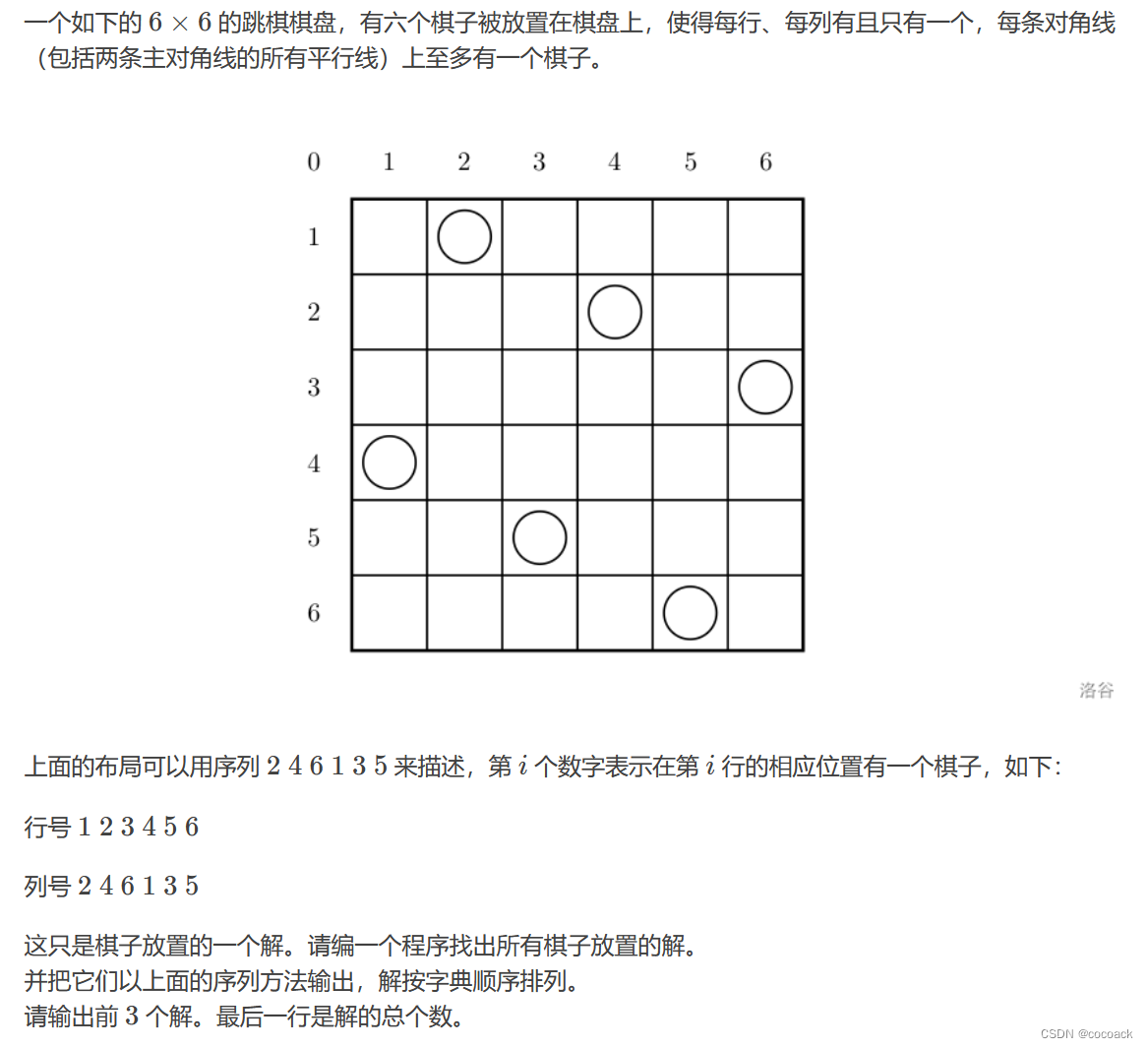
下面是分析：

我们对每行遍历一下，跟求排列差不多。在判断条件上，我们可以放一个存列的数组，对于对角线的判断，我们可以发现在主对角线上，列数-dep为恒定值，对于负数，我们平移即可。

对于副对角线，列数+DEP为恒定值，我们对着3条件判断即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,lie[15],zd[50],fd[50],a[20],cnt,sum;
void print(void){
	for(int i=1;i<=n;i++){
		cout<<a[i]<<" ";
	}
	cout<<endl;
}
void dfs(int deep){
	if(deep>n){
		cnt++;
		if(cnt<=3) print();
	}
	else{
		for(int i=1;i<=n;i++){
			if(lie[i]==0&&zd[i-deep+n]==0&&fd[i+deep]==0){
				a[deep]=i;
				lie[i]=1;
				zd[i-deep+n]=1;
				fd[i+deep]=1;
				dfs(deep+1);
				a[deep]=0;
				lie[i]=0;
				zd[i-deep+n]=0;
				fd[i+deep]=0;
			}
		}
	}
}
int main(){
	cin>>n;
	dfs(1);
	cout<<cnt;
}

接题：

下面为分析：

我们开方向数组遍历，判断条件：不出边界，不踏入同一个点（因为当你进入同一个点时，你会陷入死循环，或者从另一个角度，dfs本身就是n个for循环枚举全部可能，而进入同一个点的情况跟第一次没区别，不可能贡献另一种方案，得排除）。

下面为AC代码：

#include<bits/stdc++.h>
using namespace std;
int a[10][10];
int dir[8][2]={{-1,-2},{-2,-1},{-1,2},{2,-1},{-2,1},{2,1},{1,-2},{1,2}};
void print(void){
	for(int i=1;i<=5;i++){
		for(int j=1;j<=5;j++){
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
}
void dfs(int deep,int x,int y){
	if(deep==5*5){
		print();
		return ;
	}
	else{
		for(int i=0;i<8;i++){
			int x1=x+dir[i][0];
			int y1=y+dir[i][1];
			if(x1>5||x1<1||y1>5||y1<1) continue;
			if(a[x1][y1]==0){
				a[x1][y1]=deep+1;
				dfs(deep+1,x1,y1);
				a[x1][y1]=0;
			}
		}
	}
}

int main(){
	a[1][1]=1;
	dfs(1,1,1);
}