NOIP2013普及组T4

cnyali_cmf

已于 2024-04-02 11:57:25 修改

阅读量933

点赞数 21

CC 4.0 BY-SA版权

文章标签：算法 c++ 图论动态规划深度优先

于 2024-01-07 14:58:00 首次发布

本文链接：https://blog.youkuaiyun.com/cmf2012/article/details/135430973

文章详细解释了如何根据给定的输入格式，通过递推式和图论方法解决铁路线车站等级划分问题，给出了输入样例和输出样例，以及对应的代码实现部分。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目概述

题目描述

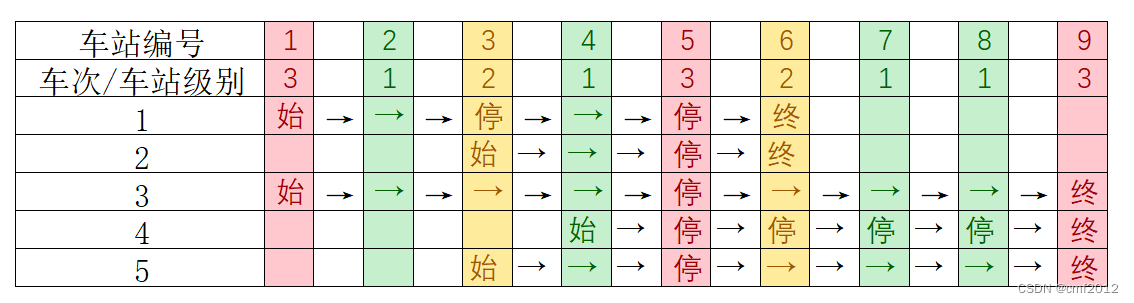
一条单向的铁路线上，依次有编号为 $1, 2, 3$ …… $, n$ 的 $n$ 个火车站。每个火车站都有一个级别，最低为 $1$ 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 $x$ ，则始发站、终点站之间所有级别大于等于火车站 $x$ 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）例如，下表是 $5$ 趟车次的运行情况。其中，前 $4$ 趟车次均满足要求，而第 $5$ 趟车次由于停靠了 $3$ 号火车站（ $2$ 级）却未停靠途经的 $6$ 号火车站（亦为 $2$ 级）而不满足要求。现有 $m$ 趟车次的运行情况（全部满足要求），试推算这 $n$ 个火车站至少分为几个不同的级别。

输入格式

第一行包含 2 个正整数 $n,m$ 用一个空格隔开。

第 $i + 1$ 行 $(1\leqslant i\leqslant m)$ 中，首先是一个正整数 $s_i (2\leqslant s_i\leqslant m)$ ，表示第 $i$ 趟车次有 $s_i$ 个停靠站；接下来有 $s_i$ 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

输出文件 $level.out$ 输出只有一行，包含一个正整数，即 $n$ 个火车站最少划分的级别数。

输入样例 1

9 2

4 1 3 5 6

3 3 5 6

输出样例1

2

输入样例2

9 3

4 1 3 5 6

3 3 5 6

3 1 5 9

输出样例2

3

解题过程

1. 理解题目

这道题的题意本来就比较抽象，不过你可以这么理解，每个火车如果停了小城市，就必须停靠大城市。例如：

假设有一条火车从上海到四川，因为停靠过中城市和大城市（起点和终点），所以南京这个大城市也一定要停靠。但是，如果我停靠了苏州但是不停靠南京，就不符合常理。而这里的城市的大小就是题目中的车站等级。

2.提意转换 (重点）

1）整体转局部

整个题目其实最难处理的部分的部分就是: “如果这趟车次停靠了火车站 $x$ ，则始发站、终点站之间所有级别大于等于火车站 $x$ 的都必须停靠。”

这显然不适合我们 DP。于是，我们转化为：停靠的站点的每一个级别一定要大于不停靠的每一个级别（注意：是大于，不是大于等于），即 $L_1 > L_2$ 。

那这有什么区别吗？一个是整体的一个规则，而另一个却是局部的，适合处理。

2）局部转图论（难点）

我们可以把每一个站点视为图上的一个点，然后在把每一个 $L_1 > L_2$ 视为一条 $L_1 \rightarrow L_2$ 的线，这样，我们便形成了一个有向图。题中第一趟火车的有向图应该长这样：

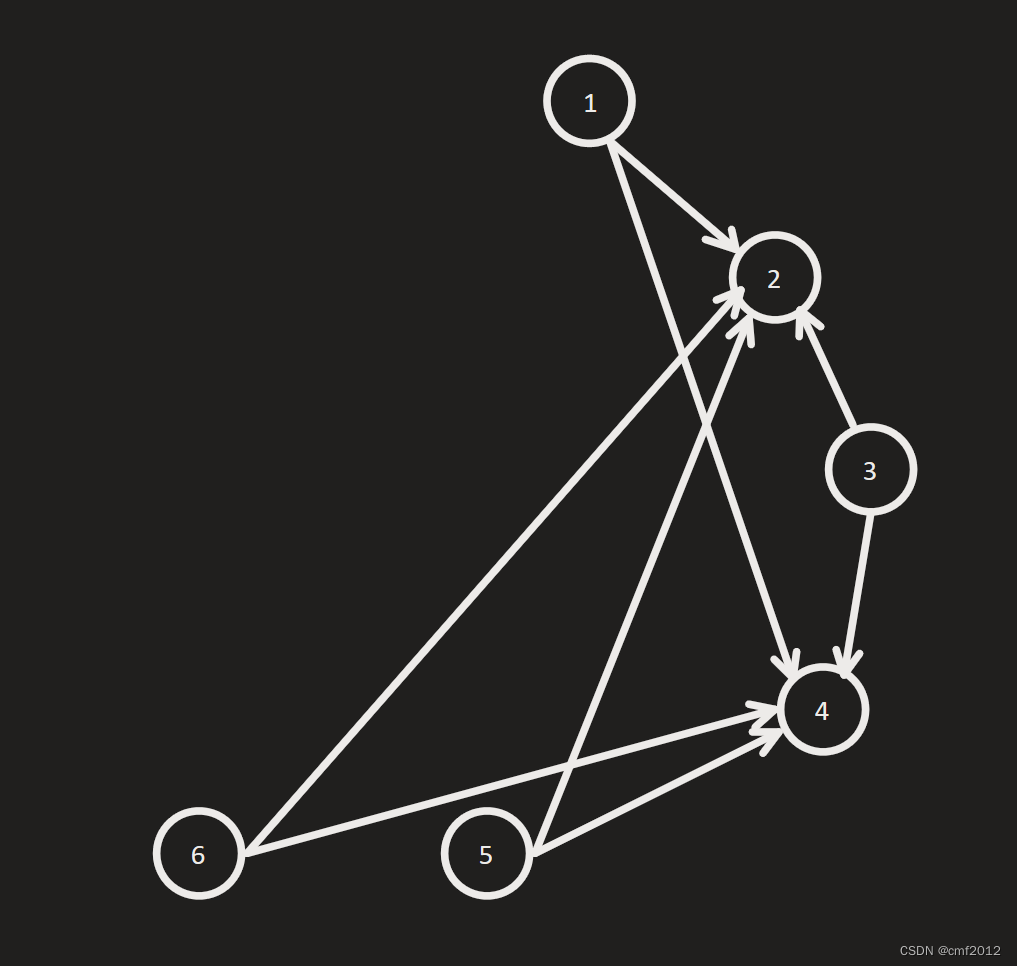
而现在，我要使得每一个箭头都成立，那不就是拓扑排序的要求吗？

BUT, $L_i$ 允许并列，所以我们把这样的并列称为拓扑独立集，即两两互不可达。

那为什叫 “独立” 集呢？如果两个一样的数，要满足上述要求，是不肯能有边的。所以它们互不可达。

3）递推式初步形成

那么，要满足这个规则，且要让车站等级最小，我们很快便能得到递推式：

$L_x = max_{x \to y}^{}L_y + 1$

我们再去递推，然后就会得到这样一张图。

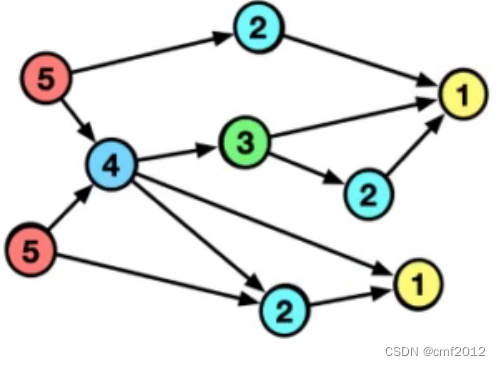
那计算顺序呢？明显是拓扑排序的逆序。

那这里要涉及到拓扑排序的内容，比较复杂。

4）进一步分析

这里我们要邀请一位嘉宾进入我们的题目

这个定理说：最短子序列覆盖 = 最长反链。至于这个定理的证明，有点复杂，请点击。

而题目的问题其实是以上的图的覆盖问题，所以我们可以把它转化为再这一个图上最长能走多远。

那么这个问题可以用 DP 就可以完美实现。

3. 代码实现

完整代码

#include<bits/stdc++.h>
using namespace std;
int N = 1005;
int main () {
	int n, m, s;
	int z [N], l [N] [N], du [N], f [N], qi;
	bool vis [N];
	queue <int> q;
	cin >> n >> m;
	for (int i = 1; i <= m; i ++) {
		cin >> s;
		memset (vis, 0, sizeof (vis));
		for (int j = 1; j <= s; j ++){
			cin >> z [j];
			vis [z [j]] = true;  
		}
		for (int j = z [1] + 1; j <= z [s];j ++) {
			if (vis [j] == false) {
				for (int k = 1; k <= s; k ++) {
					if (l [j] [z [k]] == 0){
						l [j] [z[k]] = 1;
						du [z [k]] += 1;
					}
				}
			}
		}  
	}
	for (int i = 0; i <= n - 1; i ++){
		if (du [i] == 0) {
			q.push (i);
			f [i] = 1; 
		}
	}
	while (!q.empty ()) {
		qi = q.front ();
		q.pop ();
		for (int i = 0; i <= n - 1; i ++) {
			if (l [qi] [i] == 1) {
				f [i] = max (f [qi] + 1, f [i]);
				l [qi] [i] = 0;
				du [i] -= 1;
				if (du [i] == 0) q.push(i);
			}
		}	
	}
	sort (f, f + n);
	cout << f [n - 1];
	return 0;
}