几何基础（2）向量

前言： 向量是数学、物理学和工程学等多个领域中的核心概念，它完美地将数值与几何联系在了一起。

一、向量

1、定义

向量（Vector），也称为矢量，是同时具有大小和方向的量。

2、向量的表示

2.1、几何表示

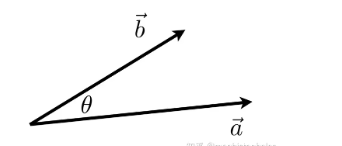
在几何中，用一个带箭头的线段来表示向量。例如：

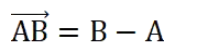
2.2、代数表示

在数学计算中，通常用一个有序的数组（坐标）来表示向量，这依赖于坐标系。

• 在二维平面（2D）：向量 v 可以表示为 (x, y)。
• 在三维空间（3D）：向量 v 可以表示为 (x, y, z)。

3、关键属性

3.1、模（Magnitude）

向量的大小或长度，对于一个n维向量 v = (v₁, v₂, ..., vₙ)，其模记作 |v|。计算公式

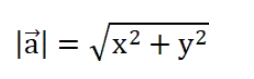
3.2、方向（Direction）

一个向量除以它自己的模，就得到一个纯表示方向的单位向量。计算公式

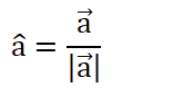
4、特殊向量

• 零向量（Zero Vector）：大小为0，方向任意。记为 0 = (0, 0) 或 (0, 0, 0)。
• 单位向量（Unit Vector）：大小为1的向量。任何非零向量都可以通过归一化转化为单位向量。单位向量通常用 ^ 符号表示。
• 负向量：与向量 v 大小相等、方向相反的向量，记为 -v。

5、基础运算

5.1、向量加法

• 几何法则：三角形法则或平行四边形法则。
  

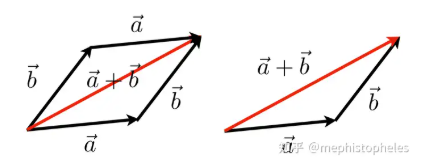
• 代数法则：对应分量相加，计算公式 (a₁, a₂) + (b₁, b₂) = (a₁ + b₁, a₂ + b₂)

5.2、向量减法

• 几何意义：v - w 可以理解为从点w指向点v的向量。
• 代数法则：对应分量相减，计算公式 (a₁, a₂) - (b₁, b₂) = (a₁ - b₁, a₂ - b₂)

5.3、标量乘法

一个向量 v 乘以一个标量 k。

• 几何意义：将向量的长度缩放为原来的 |k| 倍。
  • 如果 k > 0，新向量方向不变。
  • 如果 k < 0，新向量方向相反。
• 代数法则：向量的每个分量都乘以标量 k。计算公式 k * (v₁, v₂) = (k*v₁, k*v₂)

6、点乘（Dot Product）

点乘，也叫数量积或内积。它的运算结果是一个标量（一个数字），而不是一个向量。

6.1、代数定义

两个向量 a = (a₁, a₂, a₃) 和 b = (b₁, b₂, b₃) 的点乘，定义为它们对应分量乘积之和：
a · b = a₁b₁ + a₂b₂ + a₃b₃

6.2、几何定义

点乘的几何定义揭示了其核心意义：a · b = ||a|| × ||b|| × cos(θ) 其中：

• ||a|| 和 ||b|| 分别是向量 a 和 b 的模（长度）。
• θ 是向量 a 和 b 之间的夹角。

这个公式将纯粹的代数计算与直观的几何角度联系了起来。

6.3、使用场景

• 衡量向量间的方向相似性：

  • 如果 a · b > 0，则 θ < 90°（夹角为锐角，方向基本一致）。
  • 如果 a · b = 0，则 θ = 90°（两向量垂直）。
  • 如果 a · b < 0，则 θ > 90°（夹角为钝角，方向基本相反）。

• 计算两向量的夹角：由几何定义公式可以反推出夹角：θ = arccos( (a · b) / (||a|| ||b||) )

• 计算一个向量在另一个向量方向上的投影：向量 a 在向量 b 方向上的投影长度（标量）为：
  投影长度 = ||a|| × cos(θ) = (a · b) / ||b||

7、叉乘（Cross Product）

叉乘，也叫向量积或外积。它的运算结果是一个新的向量，而不是一个标量。叉乘通常只定义在三维空间中。

7.1、代数定义

两个向量 a = (a₁, a₂, a₃) 和 b = (b₁, b₂, b₃) 的叉乘结果是一个新向量 c = a × b = (a₂b₃ - a₃b₂, a₃b₁ - a₁b₃, a₁b₂ - a₂b₁)

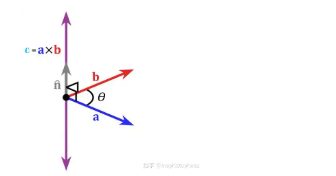
7.2、几何定义

结果向量 c = a × b 拥有两个非常重要的几何属性：

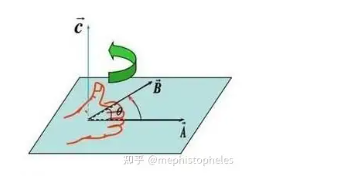
• 方向：向量 c 同时垂直于向量 a 和向量 b 所构成的平面。方向遵循右手定则，右手四指从 a 弯向 b，大拇指所指的方向就是 c 的方向。
• 模长：向量 c 的模长等于以 a 和 b 为邻边构成的平行四边形的面积。||a × b|| = ||a|| × ||b|| × sin(θ)。
  

7.3、使用场景

• 生成法向量：这是图形学中最常见的应用。已知一个平面（或三角形）上的两个不共线的向量 a 和 b，可以通过叉乘 a × b 来得到垂直于该平面的法向量。然后通常会将其归一化（转换为单位向量）后使用。
• 判断左右关系：在2D/3D中，可以通过叉积结果的正负来判断一个点是在一条线的左侧还是右侧。对于2D向量，a × b 的结果实际上是一个标量（其z分量），a × b > 0 表示 b 在 a 的左侧（逆时针方向）。
• 构建坐标系：已知一个方向（如相机的朝向 Z），可以通过叉积构造一个相互垂直的坐标系。
• 计算平行四边形/三角形的面积：叉积的模长直接就是平行四边形的面积，除以2就是三角形的面积。