<think>好的,我需要帮助用户了解Bézier曲线的插值算法及实现方法。首先,我需要明确用户的需求。用户提到了“插值”,可能是指通过给定数据点生成Bézier曲线,或者利用Bézier曲线进行插值计算。根据常见的Bézier曲线应用,插值通常指的是让曲线精确通过一组控制点,而标准的Bézier曲线通常只是逼近控制点,除了首尾端点。因此,用户可能想了解如何构造经过特定点的Bézier曲线,这可能需要使用插值方法,如多项式插值或样条方法。
接下来,我需要回顾Bézier曲线的基本知识。Bézier曲线由控制点定义,n阶曲线由n+1个控制点组成,曲线起点和终点分别与第一个和最后一个控制点重合,而中间点则不一定在曲线上。因此,如果用户希望曲线通过所有给定的数据点,可能需要采用不同的方法,比如使用三次样条插值结合Bézier曲线,或者通过反算控制点来实现插值。
根据参考中的信息,引用[1]提到Bézier曲线的递推算法,即de Casteljau算法,这可以用来计算曲线上任意点的位置。引用[3]提到Python实现Bézier曲线的例子,并指出高阶曲线计算量大的问题。这可能意味着在实现插值时,需要考虑计算效率。
现在,用户的问题是关于Bézier曲线插值算法的实现。我需要分步骤解释如何实现插值。首先,可能需要解释当数据点作为Bézier曲线的控制点时,曲线仅通过首尾点,而中间点不通过。因此,要实现插值,可能需要构造一个经过所有给定点的Bézier曲线,这通常需要反算控制点。
例如,对于三次Bézier曲线,如果给定四个点作为插值点,但通常三次Bézier曲线由四个控制点定义,但只能保证首尾点通过。因此,若要让曲线通过更多的点,可能需要使用更高阶的曲线,或者分段Bézier曲线,如Bézier样条。但这种方法可能会导致控制点数量增加,计算复杂度提高。
另一种方法是反算控制点。假设用户有一组数据点P0, P1, ..., Pn,希望构造一条Bézier曲线经过这些点。对于n次Bézier曲线,需要n+1个控制点。然而,标准的Bézier曲线仅保证首尾控制点位于曲线上,因此必须通过求解方程组来找到中间控制点的位置,使得曲线在特定参数值(如均匀分布的t值)处经过这些数据点。
例如,给定三个数据点P0, P1, P2,想要构造二次Bézier曲线经过这三个点。二次曲线有三个控制点Q0, Q1, Q2,其中Q0=P0,Q2=P2。曲线在t=0.5时为P1,根据公式B(0.5) = (Q0 + 2Q1 + Q2)/4 = P1,解得Q1 = (4P1 - P0 - P2)/2。这样,可以通过中间点P1反算出控制点Q1,从而构造出经过这三个点的二次Bézier曲线。
类似地,对于更高次数的曲线,可以建立方程组来解出控制点。但这种方法在点数较多时可能导致计算复杂度高,且方程组可能病态,需要数值方法求解。
另外,参考中的引用[3]提到分段近似,可能适用于复杂形状。因此,在实现插值时,可能需要将多个低次Bézier曲线连接起来,形成样条曲线,确保各段在连接处满足连续性条件(如C1或C2连续)。
接下来,我需要整理这些思路,分步骤解释插值算法的实现,并给出代码示例。可能需要包括:
1. 问题定义:给定一组数据点,构造Bézier曲线经过所有点。
2. 反算控制点的方法,通过建立线性方程组求解。
3. 使用de Casteljau算法计算曲线上的点。
4. 可能的优化和注意事项,如数值稳定性、分段处理等。
然后,根据用户提供的参考中的Python实现样例,可以展示一个简单的二次Bézier插值的例子,其中中间点作为插值点,反算控制点,并绘制曲线。
最后,生成相关问题,帮助用户进一步学习,如参数选择、更高阶的插值方法、与B样条的比较等。
需要确保回答结构清晰,符合用户的要求,使用中文,数学公式正确使用$...$和$$...$$,代码格式正确,并添加引用标识。</think>### Bézier曲线插值算法与实现
Bézier曲线本身是**逼近型曲线**,默认只通过首尾控制点。若需让曲线**精确通过所有给定点**,需通过数学方法反算控制点。以下是插值算法的实现步骤:
---
#### 一、Bézier曲线插值原理
对于$n$个插值点$\{P_0, P_1, \dots, P_{n-1}\}$,构造一条$n-1$次Bézier曲线,使得曲线经过所有点。控制点$\{Q_0, Q_1, \dots, Q_{n-1}\}$需满足:
$$B(t_k) = \sum_{i=0}^{n-1} Q_i \cdot B_{i}^{n-1}(t_k) = P_k \quad (k=0,1,\dots,n-1)$$
其中$B_{i}^{n-1}(t)$是Bernstein基函数,$t_k$为参数值(通常均匀分布如$t_k = \frac{k}{n-1}$)[^1]。
---
#### 二、实现步骤(以三次Bézier插值为例)
1. **输入插值点**:假设给定4个点$P_0, P_1, P_2, P_3$。
2. **建立方程组**:三次Bézier曲线方程为:
$$B(t) = (1-t)^3 Q_0 + 3t(1-t)^2 Q_1 + 3t^2(1-t) Q_2 + t^3 Q_3$$
在$t=0, 1/3, 2/3, 1$处分别对应$P_0, P_1, P_2, P_3$,生成4个方程。
3. **求解控制点**:通过线性代数方法解方程组得到$Q_0, Q_1, Q_2, Q_3$(实际$Q_0=P_0$,$Q_3=P_3$,只需解中间控制点)。
4. **生成曲线**:使用de Casteljau算法计算曲线上的点。
---
#### 三、Python代码实现
```python
import numpy as np
import matplotlib.pyplot as plt
def bezier_interpolation(points):
n = len(points)
t = np.linspace(0, 1, n)
# 构建系数矩阵
A = np.array([[B(i, n-1, t[k]) for i in range(n)] for k in range(n)])
# 解方程 A * Q = points
Q = np.linalg.solve(A, points)
return Q
def B(i, n, t):
# Bernstein基函数
return np.math.comb(n, i) * (t**i) * ((1 - t)**(n - i))
# 示例:插值4个点
points = np.array([[0, 0], [2, 3], [5, 4], [7, 1]])
Q = bezier_interpolation(points)
# 绘制曲线
t_vals = np.linspace(0, 1, 100)
curve = np.array([sum(Q[i] * B(i, 3, t) for i in range(4)) for t in t_vals])
plt.plot(curve[:,0], curve[:,1], 'b-', label='Bézier Curve')
plt.plot(points[:,0], points[:,1], 'ro--', label='插值点')
plt.legend()
plt.show()
```
---
#### 四、关键问题与优化
1. **参数选择**:均匀参数可能导致曲线震荡,可使用弦长参数化法优化$t$分布。
2. **分段插值**:对大量插值点,使用分段三次Bézier曲线并保证连接处光滑(如C1连续)[^3]。
3. **数值稳定性**:高阶矩阵求逆可能不稳定,建议限制阶数(如≤5)或使用B样条替代。
---

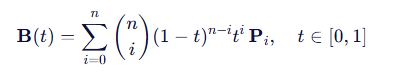


 贝塞尔曲线及其算法应用
贝塞尔曲线及其算法应用





















 497
497

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








