心形线汇总-数学曲线的浪漫表白（进阶版）_latex排版心形线我爱数学-优快云博客

昨天，小编为大家介绍了4中常见的心形线方程。今天再带给大家2种心形线，作图难度较大，需要一定的编程思想和解方程技巧，得到的图像也非常美观。

5. 心形线-立体版

方程为：

$\left( \it{x}\rm{^2+}\frac{9}{4}\it{y}\rm{^2+}\it{z}\rm{^2-1} \right) ^3- \it{x}\rm{^2}\it{z}\rm{^3} - \frac{9}{80}\it{y}\rm{^2}\it{z}\rm{^3} =0$

这里x和z分别对应心形的宽和高，也就是二位心形的x和y坐标，而z代表了心形的“厚度”维度。

这种曲面很难求解，因此我们直接使用MATLAB的isosurface函数作图。代码和作图结果如下：

声明：该代码适当参考了“数学中国”微信公众号2017.8.17的文章，并进行了修改。

clear; close all;
% 心形线-立体曲面版
f=@(x,y,z)(x.^2+9/4*y.^2+z.^2-1).^3 - x.^2.*z.^3 - 9/80*y.^2.*z.^3;
[x,y,z]=meshgrid(linspace(-1.5,1.5,76));
val=f(x,y,z);
equation=['$$\left( \it{x}\rm{^2+}\frac{9}{4}\it{y}\rm{^2+}\it{z}\rm{^2-1} \right) ^3'...
    '- \it{x}\rm{^2}\it{z}\rm{^3} - \frac{9}{80}\it{y}\rm{^2}\it{z}\rm{^3} =0$$'];

c=figure;
isosurface(x,y,z,val,0);
view(3); grid on; axis equal; colormap([1 0.2 0.2]);
xlabel('\it{x}','FontName','Times New Roman','FontSize',15);
ylabel('\it{y}','FontName','Times New Roman','FontSize',15);
zlabel('\it{z}','FontName','Times New Roman','FontSize',15);
c.InnerPosition=[400 100 500 400];
xlim([-1.5,1.5]); ylim([-1,1]); zlim([-1,1.5]);
xticks(-1.5:0.5:1.5); yticks(-1:0.5:1); zticks(-1:0.5:1.5);
c.CurrentAxes.FontName='Times New Roman';
text(-1.7,1,2,equation,'Interpreter','latex','FontSize',15);

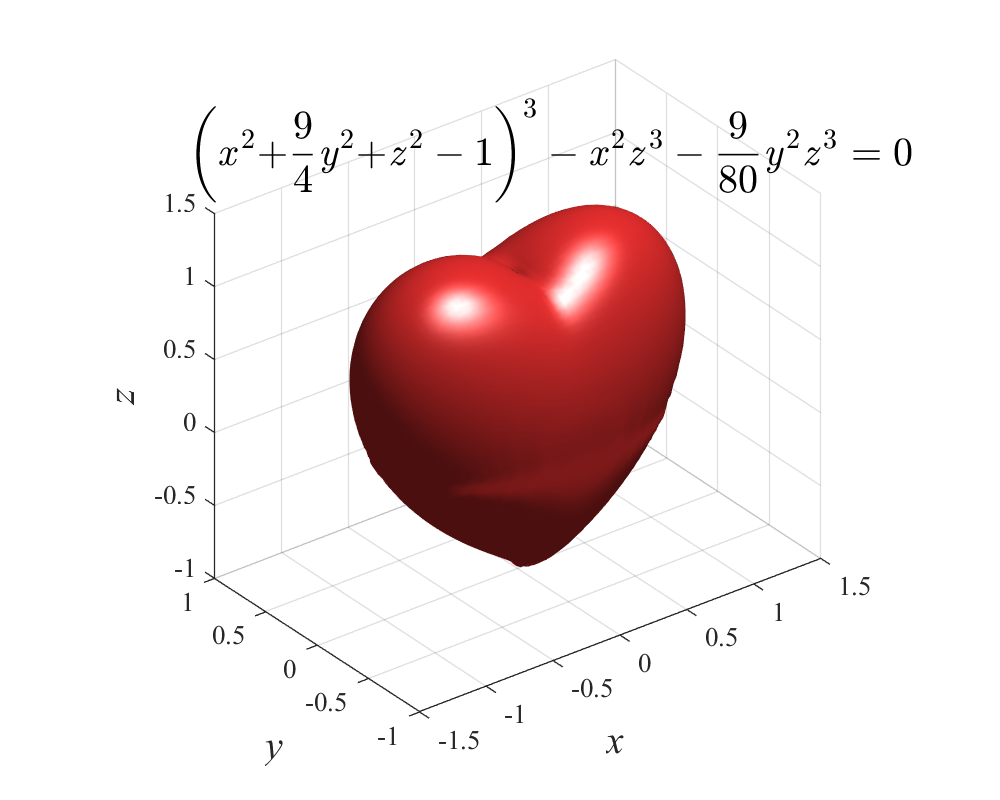
图像还是挺漂亮的。

为了更清晰的看到心形曲面的透视结构，还可以画成网格面的效果，作图代码如下：

clear; close all;
% 心形线-立体网面版
f=@(x,y,z)(x.^2+9/4*y.^2+z.^2-1).^3 - x.^2.*z.^3 - 9/80*y.^2.*z.^3;
[x,y,z]=meshgrid(linspace(-1.5,1.5,76));
val=f(x,y,z);
[p,v]=isosurface(x,y,z,val,0);
equation=['$$\left( \it{x}\rm{^2+}\frac{9}{4}\it{y}\rm{^2+}\it{z}\rm{^2-1} \right) ^3'...
    '- \it{x}\rm{^2}\it{z}\rm{^3} - \frac{9}{80}\it{y}\rm{^2}\it{z}\rm{^3} =0$$'];

c=figure;
patch('faces',p,'vertices',v,'facevertexcdata',jet(size(v,1)),'facecolor','w','edgecolor','flat');
view(3); grid on; axis equal;
xlabel('\it{x}','FontName','Times New Roman','FontSize',15);
ylabel('\it{y}','FontName','Times New Roman','FontSize',15);
zlabel('\it{z}','FontName','Times New Roman','FontSize',15);
c.InnerPosition=[400 100 500 400];
xlim([-1.5,1.5]); ylim([-1,1]); zlim([-1,1.5]);
xticks(-1.5:0.5:1.5); yticks(-1:0.5:1); zticks(-1:0.5:1.5);
c.CurrentAxes.FontName='Times New Roman';
text(-1.7,1,2,equation,'Interpreter','latex','FontSize',15);

效果也更加绚丽：

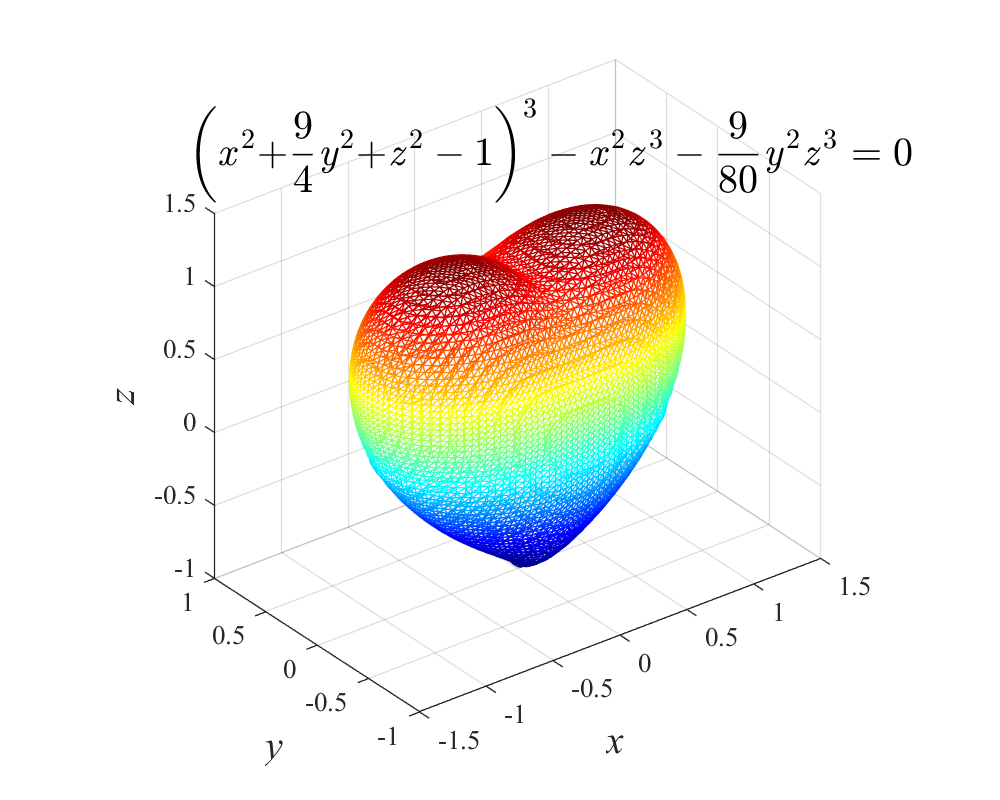
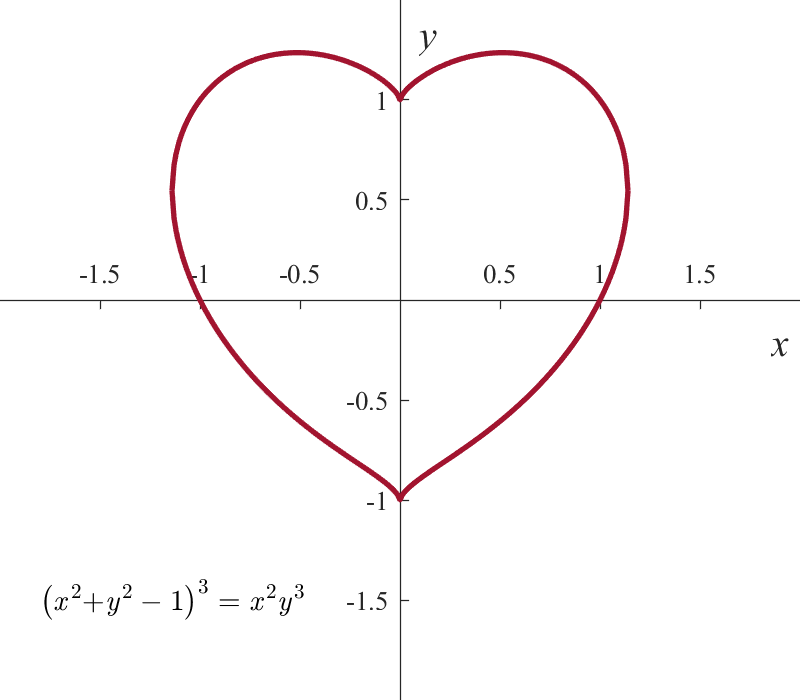
6. 另一种平面心形线

方程为：

$\left(\it{x}\rm{^2+}\it{y}\rm{^2-1}\right) ^3 = \it{x}\rm{^2}\it{y}\rm{^3}$

为了求解方程，首先移项得

$\left(x^2+y^2-1\right)^3-x^2 y^3=0$

不难看出，这就是上面那种“立体”心形取y=0剖面、并将z维度换回平面直角坐标的y的情形。利用立方差公式，分解因式得

$\left( y^2-\left(x^2\right)^{1/3} y+x^2-1 \right) \left[ \left(x^2+y^2-1\right)^2+ \left(x^2+y^2-1\right) \left(x^2\right)^{1/3} y+\left(x^2\right)^{2/3} y^2 \right]=0$

右边的因式等于0时没有实数解，我们只需关注左边的因式，令其等于0：

$y^2-\left(x^2\right)^{1/3} y+x^2-1=0$

利用二次方程求根公式得

$\left\{\begin{matrix} y_1=\frac{\left(x^2\right)^{1/3} + \sqrt{\left(x^2\right)^{2/3}-4x^2+4}} {2} \\y_2=\frac{\left(x^2\right)^{1/3} - \sqrt{\left(x^2\right)^{2/3}-4x^2+4}} {2} \end{matrix}\right.$

它们分别对应心形线的上下两部分。

MATLAB作图代码和作图结果如下：

clear; close all;
% 心形线
x=-2:0.01:2;
x2=x.^2;
sqrt_part=sqrt(x2.^(2/3)-4*x2+4);

y1=(x2.^(1/3)+sqrt(x2.^(2/3)-4*x2+4))/2;
y2=(x2.^(1/3)-sqrt(x2.^(2/3)-4*x2+4))/2;
start=find(imag(y1)==0,1)-1; End=length(x)-start+1;
% strat和End是y坐标数组具有几何意义（即y是实数）的边界，边界向外加1以避免上下曲线衔接处中断
x=x(start:End);
y1=y1(start:End); y1=real(y1);
y2=y2(start:End); y2=real(y2);
equation={'$$\left(\it{x}\rm{^2+}\it{y}\rm{^2-1}\right) ^3 = \it{x}\rm{^2}\it{y}\rm{^3}$$'};

c=figure;
plot(x,y1,x,y2,'Color','#A2142F','LineWidth',2);
xlabel('\it{x}','FontName','Times New Roman','FontSize',15);
ylabel('\it{y}','FontName','Times New Roman','FontSize',15);
c.InnerPosition=[400 100 400 350];
c.Resize="off";
xlim([-2,2]); ylim([-2,1.5]);
xticks(-1.5:0.5:1.5); yticks(-1.5:0.5:1);
c.CurrentAxes.XAxisLocation='origin';
c.CurrentAxes.YAxisLocation='origin';
c.CurrentAxes.InnerPosition=[0,0,1,1];
c.CurrentAxes.Box='off';
c.CurrentAxes.FontName='Times New Roman';
text(-1.8,-1.5,equation,'Interpreter','latex','FontSize',11);