DFS实现组合型枚举和排列型枚举

亲爱的朋友们,5个数中选择三个数,有多少种组合方式,请你列举出来,这个对于我们人来说很容易,比如1-5中选三个数,有如下情况

1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

那么,如何用代码去实现呢?             

很显然,需要利用深搜去写,逐个逐个地列举所有情况,具体怎么写,请看如下代码.

# include<iostream>
# include<bits/stdc++.h>
using namespace std;
vector<int>  chosen;
int n, m;
void cal(int deep) {


	if (chosen.size() > m || chosen.size() + (n - deep + 1) < m) {
		return;
	}
	if (deep == n + 1) {
		for (int i = 0; i < chosen.size(); i++) {
			cout << chosen[i] << ' ';
		}
		cout << endl;
		return;
	}
	chosen.push_back(deep);
	cal(deep + 1);
	chosen.pop_back();
	cal(deep + 1);
}

int main() {

	cin >> n >> m;
	// 从n个中选出m个
	cal(1);
	return 0;

}

这是一个原始模板的代码,笔者接下来将逐步拆解.

首先是存储深度的

vector<int>  chosen;

建立一个vector,负责存储深度,换句话说,存下标,如果你想要输出别的,vector可以当作下标使用,上面的代码直接把下标输出了,

然后是剪枝部分

	if (chosen.size() > m || chosen.size() + (n - deep + 1) < m)
    {
		return;
	}

有两种情况需要被剪枝,第一种,选择数量已经大于我需要的数量m了,第二种情况,我已经选好的,加上还没有选的,即(总数-当前深度+1),还凑不出需要的数量m,那也可以剪枝了.

主代码部分

if (deep == n + 1) {
		for (int i = 0; i < chosen.size(); i++) {
			cout << chosen[i] << ' ';
		}
		cout << endl;
		return;
	}
	chosen.push_back(deep);
	cal(deep + 1);
	chosen.pop_back();
	cal(deep + 1);

满足条件,就输出.然后将深度(下标)存入vector,接着继续遍历下一层.

此时,有两种情况.

情况一:不需要被剪枝,也不需要被输出,那么就一直遍历下去,直到可以被输出,然后return回来,然后将这一层pop_back(),从下一层遍历;

情况二:需要被剪枝了,那么此时,说明当前的层数已经不符合条件了,那么也pop_back(),当前层数,

然后继续遍历下一层情况,

请记住,vector存储的是下标,是深度!

实例代码最后的效果如图

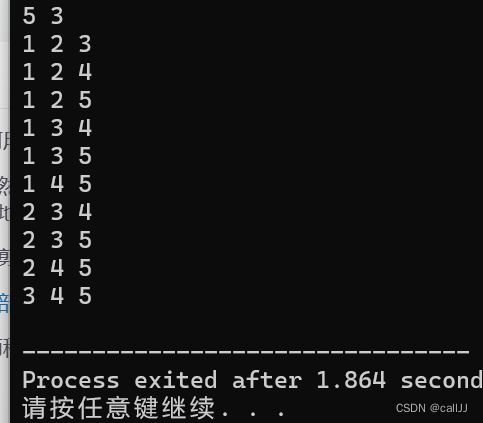
 笔者是蓝桥杯B,C++组,有一题就好像需要这么写加上gcd和lcm公式

因为笔者其他题都是狗屎,也许笔者也就是靠这道题,这个写法,才混了个头部省二的位置.

这道题和初学dfs时,用dfs写排列一样,不过笔者这个是组合而已,难度稍微高了一点点

排列型枚举

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
//dfs实现排列型枚举（模板）
public class Main {
    static List<Integer> list = new ArrayList<>();
    static int n;
    static boolean[] vis;  // 用于标记元素是否已经被选中过
    // 递归生成排列
    static void DFS(int deep) {
        if (deep == n + 1) {
            // 输出一个排列
            for (Integer i : list) {
                System.out.print(i + " ");
            }
            System.out.println();
            return;
        }
        // 遍历所有的元素，生成排列
        for (int i = 1; i <= n; i++) {
            if (!vis[i]) {  // 如果元素i还没有被使用
                vis[i] = true;  // 标记元素i已经被使用
                list.add(i);  // 将元素i加入当前排列
                DFS(deep + 1);  // 继续递归
                list.remove(list.size() - 1);  // 回溯，移除当前元素
                vis[i] = false;  // 回溯，标记元素i未被使用
            }
        }
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();  // 输入 n
        vis = new boolean[n + 1];  // 初始化 vis 数组，大小为 n+1，因为元素是从 1 到 n
        DFS(1);  // 从1开始递归
    }
}