C#判断一个矩阵是否为对称矩阵、反称矩阵

对称与反称矩阵判断

最新推荐文章于 2025-11-27 14:05:49 发布

转载最新推荐文章于 2025-11-27 14:05:49 发布 · 1.4k 阅读

3 ·

CC 4.0 BY-SA版权

原文链接：https://my.oschina.net/Tsybius2014/blog/224905

文章标签：

#c#

本文介绍如何通过编程方式判断一个矩阵是否为对称矩阵或反称矩阵，并提供了具体的实现代码及示例运行结果。

部署运行你感兴趣的模型镜像

1.判断对称矩阵

对任意i和j，有a[i,j]=a[j,i]

/// <summary>
/// 检查一个矩阵是否为对称矩阵
/// </summary>
/// <param name="matrix">矩阵</param>
/// <returns>true：是对称矩阵 false：不是对称矩阵</returns>
private static bool isSymmetric(double[][] matrix)
{
    //矩阵没有元素的情况
    if (matrix.Length == 0)
    {
        return true;
    }

    //合法性检查：1）matrix应为矩阵；2）matrix应为方阵
    if (!isMatrix(matrix) || matrix.Length != matrix[0].Length)
    {
        throw new Exception("输入不合法");
    }

    //矩阵对称条件：对任意i,j有a[i,j]=a[j,i]
    for (int i = 0; i < matrix.Length; i++)
    {
        for (int j = 0; j < i; j++)
        {
            if (matrix[i][j] != matrix[j][i])
            {
                return false;
            }
        }
    }

    return true;
}

2.判断反称矩阵

对任意i和j，有a[i,j]=-a[j,i]

/// <summary>
/// 检查一个矩阵是否为反称矩阵
/// </summary>
/// <param name="matrix">矩阵</param>
/// <returns>true：是反称矩阵 false：不是反称矩阵</returns>
private static bool isSkewSymmetric(double[][] matrix)
{
    //矩阵没有元素的情况
    if (matrix.Length == 0)
    {
        return true;
    }

    //合法性检查：1）matrix应为矩阵；2）matrix应为方阵
    if (!isMatrix(matrix) || matrix.Length != matrix[0].Length)
    {
        throw new Exception("输入不合法");
    }

    //矩阵反称条件：对任意i,j有a[i,j]=-a[j,i]
    for (int i = 0; i < matrix.Length; i++)
    {
        for (int j = 0; j <= i; j++)
        {
            if (matrix[i][j] != -matrix[j][i])
            {
                return false;
            }
        }
    }

    return true;
}

3.相关函数

/// <summary>
/// 判断一个二维数组是否为矩阵
/// </summary>
/// <param name="matrix">二维数组</param>
/// <returns>true:是矩阵 false:不是矩阵</returns>
private static bool isMatrix(double[][] matrix)
{
    //空矩阵是矩阵
    if (matrix.Length < 1) return true;

    //不同行列数如果不相等，则不是矩阵
    int count = matrix[0].Length;
    for (int i = 1; i < matrix.Length; i++)
    {
        if (matrix[i].Length != count)
        {
            return false;
        }
    }

    //各行列数相等，则是矩阵
    return true;
}

4.函数调用示例

1）Main函数代码

static void Main(string[] args)
{
    //测试矩阵1：matrix1
    double[][] matrix1 = new double[][] 
    {
        new double[] { 1, 2, 3 },
        new double[] { 2, 1, 2 },
        new double[] { 3, 2, 1 }
    };

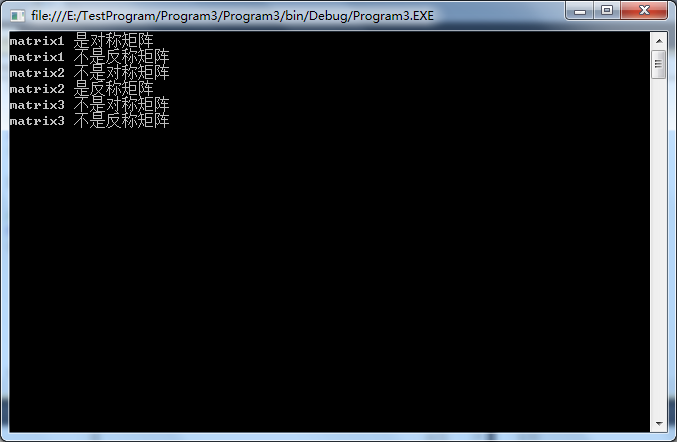
    if (isSymmetric(matrix1)) { Console.WriteLine("matrix1 是对称矩阵"); }
    else { Console.WriteLine("matrix1 不是对称矩阵"); }
    if (isSkewSymmetric(matrix1)) { Console.WriteLine("matrix1 是反称矩阵"); }
    else { Console.WriteLine("matrix1 不是反称矩阵"); }

    //测试矩阵2：matrix2
    double[][] matrix2 = new double[][] 
    {
        new double[] { 0, 1, 2 },
        new double[] { -1, 0, 1 },
        new double[] { -2, -1, 0 }
    };

    if (isSymmetric(matrix2)) { Console.WriteLine("matrix2 是对称矩阵"); }
    else { Console.WriteLine("matrix2 不是对称矩阵"); }
    if (isSkewSymmetric(matrix2)) { Console.WriteLine("matrix2 是反称矩阵"); }
    else { Console.WriteLine("matrix2 不是反称矩阵"); }

    //测试矩阵3：matrix3
    double[][] matrix3 = new double[][] 
    {
        new double[] { 1, 2, 3 },
        new double[] { 4, 5, 6 },
        new double[] { 7, 8, 9 }
    };

    if (isSymmetric(matrix3)) { Console.WriteLine("matrix3 是对称矩阵"); }
    else { Console.WriteLine("matrix3 不是对称矩阵"); }
    if (isSkewSymmetric(matrix3)) { Console.WriteLine("matrix3 是反称矩阵"); }
    else { Console.WriteLine("matrix3 不是反称矩阵"); }

    Console.ReadLine();
}

2）示例运行结果