小白也能看懂的深度学习6

最近思如泉涌，那我们趁热打铁，再学一点。

2.14向量化 logistic 回归的梯度输出

如何向量化计算的同时，对整个训练集预测结果，这是我们之前已经讨论过的内容。

在这篇文章我们将学习如何向量化地计算m个训练数据的梯度，重点是如何同时计算 m个数据的梯度，并且实现一个非常高效的逻辑回归算法。

当然，这里的推导有一定意义，但是如果你正在使用像TensorFlow或者PyTorch这样的深度学习框架，这些库内部已经实现了自动微分机制，可以直接给出所需的梯度而无需手动推导。

所以理解就好。我们再来理一下脉络：

首先，Logistic回归是一个分类模型，用来预测二分类的概率。它的假设函数是sigmoid函数，也就是hθ(x) = 1/(1 + e(-θT x))，这里的θ是参数向量，x是特征向量。我们的目标是通过训练数据找到合适的θ，使得预测结果尽可能准确。

在训练过程中，我们需要定义一个损失函数，通常使用的是对数损失函数。对于m个样本的情况，损失函数J(θ)可以写成平均的损失，也就是：
J(θ) = (-1/m) * Σ [y_i * log(hθ(x_i)) + (1 - y_i) * log(1 - hθ(x_i))]
这里的求和是对所有样本i=1到m进行的。

现在，为了用梯度下降法来优化参数θ，我们需要计算损失函数对每个参数θ_j的偏导数，也就是梯度。然后根据梯度来更新θ_j，直到收敛。

如果是非向量化的方式，也就是逐个样本计算的话，梯度下降的更新规则可能是这样的：对于每个θ_j，计算梯度项，然后累加所有样本的梯度，再取平均，然后乘以学习率α，最后用这个来更新θ_j。这可能在数据量大时效率很低，所以我们需要向量化的实现来提高计算效率。

那向量化的梯度计算具体是怎样的呢？

首先，向量化的操作通常涉及矩阵和向量的运算，避免显式的循环。

假设我们的输入数据X是一个m×n的矩阵，其中m是样本数量，n是特征数量（包括偏置项，如果有的话）。参数θ是一个n×1的列向量。那么，假设函数hθ(X)可以表示为sigmoid(Xθ)，也就是对每个样本计算θ^T x_i的结果，然后应用sigmoid函数。这里Xθ的结果是一个m×1的向量，每个元素对应一个样本的线性组合结果。
接下来，计算损失函数的时候，y是真实的标签，是m×1的向量。

那么，hθ(X)和y之间的差异应该是一个m×1的向量，每个元素是hθ(x_i) - y_i。

这个时候，梯度应该是如何计算的呢？
在Logistic回归中，参数的梯度计算可以简化成某种矩阵运算。

比如，对于所有样本，梯度的计算可以表示为X的转置乘以（h - y）然后除以m，也就是 (1/m) * X^T (h - y)，其中h是sigmoid(Xθ)的结果。这样的话，整个梯度向量就可以一次性计算出来，而不需要逐个特征或逐个样本进行循环。

大致就是这样的思路，最后我们能得到的就是这个式子

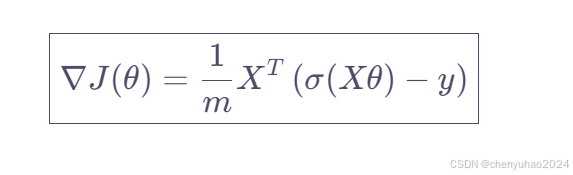
好了大致理解就行。可能会很深奥，如果你看不懂的话还是建议去b站搜一下相关的视频看看推导过程。好，这篇文章到这里就结束了，下一篇我们将深入讲解广播机制以及广播在numpy里面的运用。感谢阅读！如果你也打算学习深度学习，可以给我点个关注。或者看看往期的文章。