从L1到L3：程序员必须掌握的CPU缓存优化实战手册

目录

要弄清cpu，先搞懂内存

为什么会设计成三层？

多级内存的问题

缓存的命中

​编辑

缓存的一致性

程序实战测试

示例一

示例二

---

前言：在计算机系统中，CPU高速缓存(英语：CPU Cache，在本文中简称缓存)是用于减少处理器访问内存所需平均时间的部件。在金字塔式存储体系中它位于自顶向下的第二层，仅次于CPU寄存器。其容量远小于内存，但速度却可以接近处理器的频率。当处理器发出内存访问请求时，会先查看缓存内是否有请求数据。如果存在(命中)，则不经访问内存直接返回该数据;如果不存在(失效)，则要先把内存中的相应数据载入缓存，再将其返回处理器。缓存之所以有效，主要是因为程序运行时对内存的访问呈现局部性(Locality)特征。这种局部性既包括空间局部性(Spatial Locality)，也包括时间局部性(Temporal Locality)。有效利用这种局部性，缓存可以达到极高的命中率。在处理器看来，缓存是一个透明部件。因此，程序员通常无法直接干预对缓存的操作。但是，确实可以根据缓存的特点对程序代码实施特定优化，从而更好地利用缓存。

那么本篇文章，小编就和大家一起来探讨关于CPU缓存优化的深层知识，来帮助大家写出效率更高性能更优的代码。

要弄清cpu，先搞懂内存

现在，计算机具有两种不同类型的内存：
⭐一种类型是在RAM模块中使用的类型，它是DRAM或动态RAM，DRAM是一种使用电容器存储数据的存储器，这些电容器必须经常用电，不断地动态更新，以存储数据。
⭐但是，计算机使用的另外一种类型的内存，不必经常刷新。这种存储器被称为SRAM或静态RAM，SRAM是cpu缓存中使用的。而且由于不必不断刷新SRAM，因此它比DRAM快很多，而且价格也很昂贵。

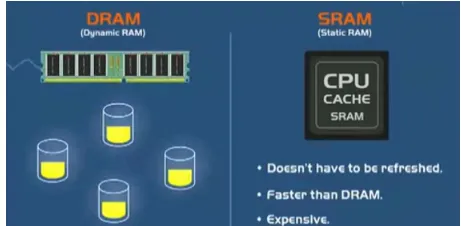
这个可以仅作了解，对于理解cpu有更全面系统的帮助，我们还是回归我们的主题cpu上来。

首先，我们都知道现在的CPU多核技术，都会有几级缓存，老的CPU会有两级内存（L1和L2），新的CPU会有三级内存（L1，L2，L3 ），如下图所示：

 

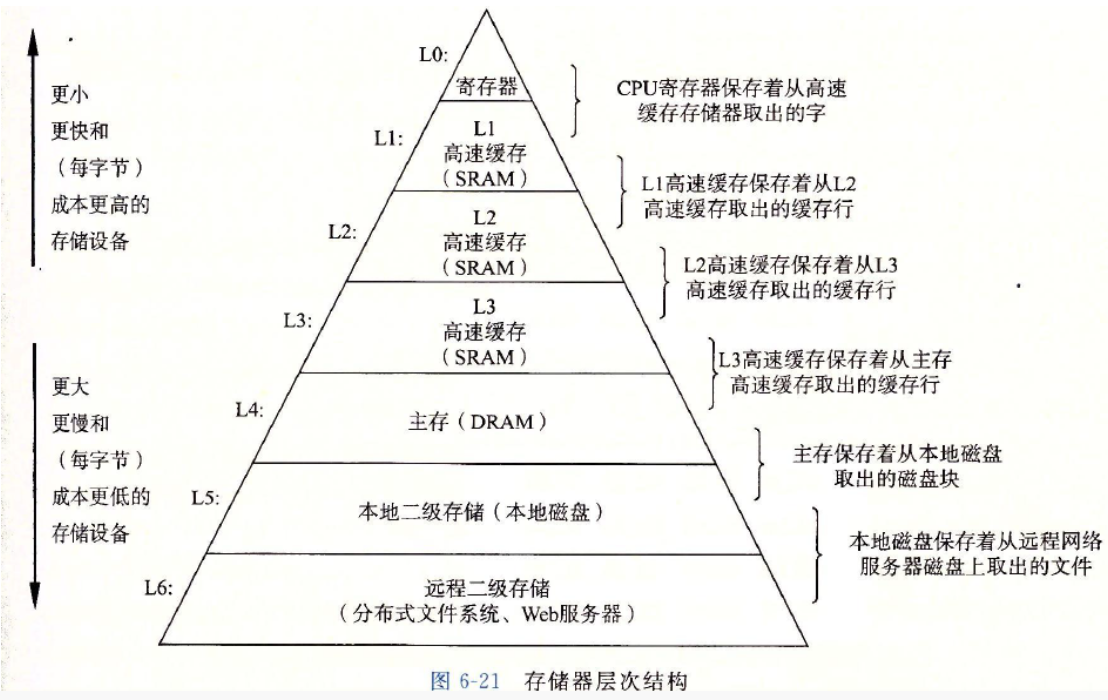
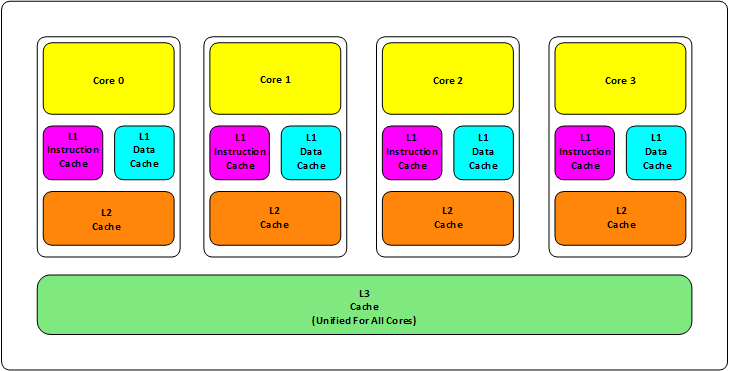
这里有两种画法，不过不同的画法代表的就是在内存处理上不同的理解，这里还是要比较一下二者的区别。

其中:

L1缓存分成两种，一种是指令缓存，一种是数据缓存。L2缓存和L3缓存不分指令和数据。
L1和L2缓存在每一个CPU核中，L3则是所有CPU核心共享的内存。
L1、L2、L3的越离CPU近就越小，速度也越快，越离CPU远，速度也越慢。

一级缓存，也被称为主缓存，一级缓存位于处理器本身上。因此，它的运行速度与处理器相同，非常快，是计算机上最快的缓存。

还有二级缓存，也被称为外部缓存，二级缓存用来捕获来自处理器的，未被一级缓存捕获的最近数据访问。

因此，简而言之，如果cpu在一级缓存中找不到所需的数据，则它将在二级缓存中搜索该数据。而且，如果cpu在二级缓存中找不到数据，则它将搜索最后一级的三级缓存。三级缓存用于捕获二级缓存未捕获的最近数据访问。最后，如果第三级缓存没有数据，那么cpu必须回到较慢的RAM才能找到所需的数据。

下面这张图就非常清晰了：

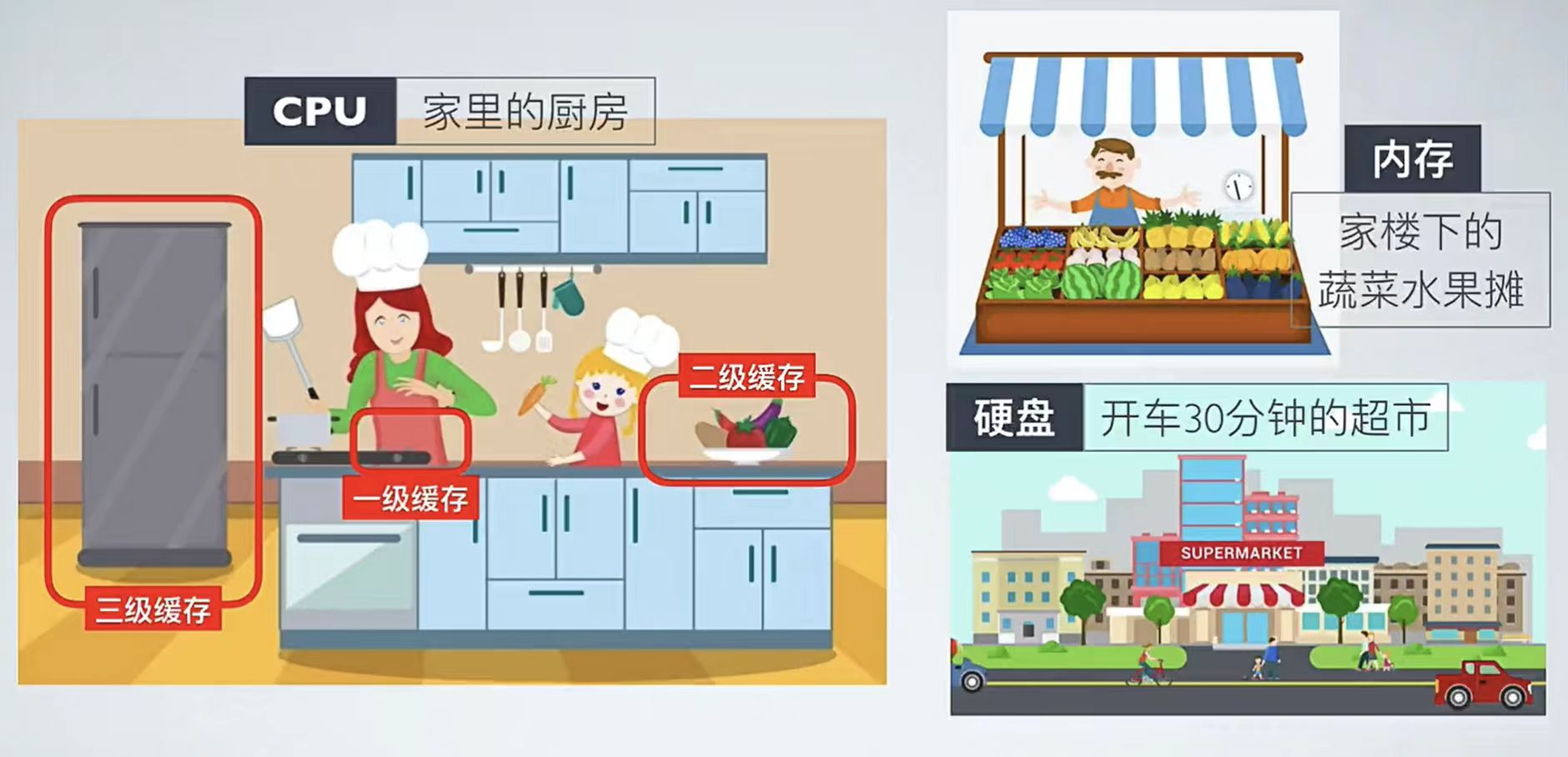
再往后面就是内存，内存的后面就是硬盘。我们来看一些他们的速度：

*L1 的存取速度：4 个CPU时钟周期
*L2 的存取速度： 11 个CPU时钟周期
*L3 的存取速度：39 个CPU时钟周期
*RAM内存的存取速度：107 个CPU时钟周期

我们可以看到，L1的速度是RAM的27倍，但是L1/L2的大小基本上也就是KB级别的，L3会是MB级别的。例如：Intel Core i7-8700K ，是一个6核的CPU，每核上的L1是64KB（数据和指令各32KB），L2 是 256K，L3有2MB.

我们的数据就从内存向上，先到L3，再到L2，再到L1，最后到寄存器进行CPU计算。

为什么会设计成三层？

这里有下面几个方面的考虑：

一个方面是物理速度，如果要更大的容量就需要更多的晶体管，除了芯片的体积会变大，更重要的是大量的晶体管会导致速度下降，因为访问速度和要访问的晶体管所在的位置成反比，也就是当信号路径变长时，通信速度会变慢。这部分是物理问题。
另外一个问题是，多核技术中，数据的状态需要在多个CPU中进行同步，并且，我们可以看到，cache和RAM的速度差距太大，所以，多级不同尺寸的缓存有利于提高整体的性能。

多级内存的问题

这个世界永远是平衡的，一面变得有多光鲜，另一面也会变得有多黑暗。建立这么多级的缓存，一定就会引入其它的问题，这里有两个比较重要的问题:

一个是比较简单的缓存的命中率的问题。
另一个是比较复杂的缓存更新的一致性问题。

缓存的命中

在说明这两个问题之前。我们需要要解一个术语 Cache Line。缓存基本上来说就是把后面的数据加载到离自己近的地方，对于CPU来说，它是不会一个字节一个字节的加载的，因为这非常没有效率，一般来说都是要一块一块的加载的，对于这样的一块一块的数据单位，术语叫“Cache Line”，一般来说，一个主流的CPU的Cache Line 是 64 Bytes（也有的CPU用32Bytes和128Bytes），64Bytes也就是16个32位的整型，这就是CPU从内存中捞数据上来的最小数据单位。

比如：Cache Line是最小单位（64Bytes），所以先把Cache分布在多个Cache Line里面，比如：L1有32KB，那么，32KB/64B = 512 个 Cache Line。

一方面，缓存需要把内存里的数据放到放进来，英文叫 CPU Associativity。Cache的数据放置的策略决定了内存中的数据块会拷贝到CPU Cache中的哪个位置上，因为Cache的大小远远小于内存，所以，需要有一种地址关联的算法，能够让内存中的数据可以被映射到Cache中来。这个有点像内存地址从逻辑地址向物理地址映射的方法，但不完全一样。

所以我们想出来了两种方法

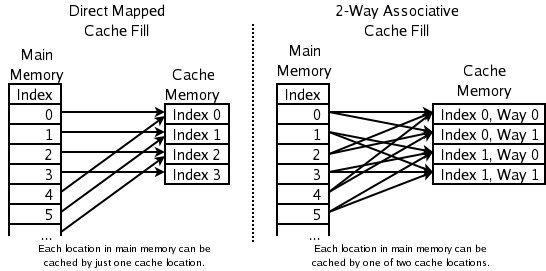
一种方法是，任何一个内存地址的数据可以被缓存在任何一个Cache Line里，这种方法是最灵活的，但是，如果我们要知道某一个内存是否存在于Cache中，我们就需要进行O(n)复杂度的Cache遍历，这是很没有效率的。

另一种方法，为了降低缓存搜索算法，我们要用一种“求模运算的思想”，比如：我们的L1 Cache有512个Cache Line，那么，公式：（内存地址 mod 512）* 64 就可以直接找到所在的Cache地址的偏移了。但是，这样的方式需要我们的程序对内存地址的访问要非常地平均，不然，就会出大问题，这导致这种情况就成了一种非常理想的情况了。

所以我们为了避免这两种情况，新想出了一种办法叫Set Associativity

也就是把连续的N个Cache Line绑成一组，然后，先把找到相关的组，然后再在这个组内找到相关的Cache Line。

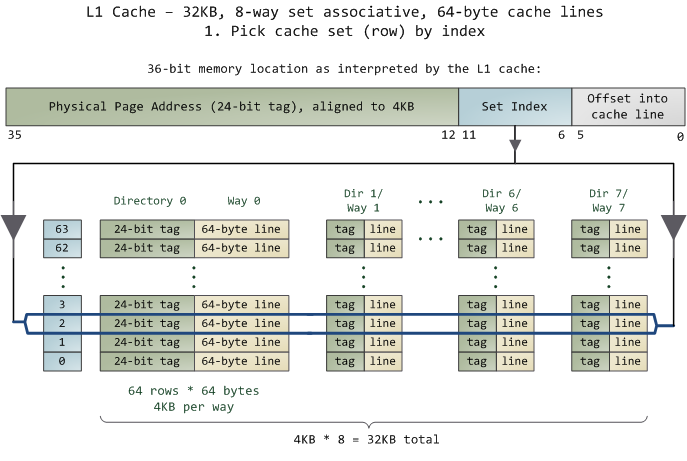
 我们看到图片里很像我们曾经学习过的函数指针数组，也就是一个数组套数组嘛，那这里当拿到一个内存地址的时候，先拿出中间的 6bits 来，找到是哪组。然后，在这一个8组的cache line中，再进行遍历，主是要匹配前24bits的tag。如果匹配中了，就算命中，如果没有匹配到，那就是miss，当然如果是读取操作，就需要进向后面的缓存进行访问了。

L2/L3同样是这样的算法。而淘汰算法有两种，一种是随机一种是LRU。

所以这也意味着：

1.L1 Cache 可映射 36bits 的内存地址，一共 2^36 = 64GB的内存
2.当CPU要访问一个内存的时候，通过这个内存中间的6bits 定位是哪个set，通过前 24bits 定位相应的Cache Line。
3.就像一个hash Table的数据结构一样，先是O(1)的索引，然后进入冲突搜索。
4.因为中间的 6bits 决定了一个同一个set，所以，对于一段连续的内存来说，每隔4096的内存会被放在同一个组内，导致缓存冲突。

了解这些细节，会有利于我们知道在什么情况下有可以导致缓存的失效。

缓存的一致性

对于主流的CPU来说，缓存的写操作基本上是两种策略：

1.一种是Write Back，写操作只要在cache上，然后再冲洗到内存上。

2.一种是Write Through，写操作同时写到cache和内存上。

为了提高写的性能，一般来说，主流的CPU采用的是Write Back的策略，因为直接写内存实在是太慢了。

好了，现在问题来了，如果有一个数据 x 在 CPU 第0核的缓存上被更新了，那么其它CPU核上对于这个数据 x 的值也要被更新，这就是缓存一致性的问题。

一般来说，在CPU硬件上，会有两种方法来解决这个问题。

1.Directory 协议。这种方法的典型实现是要设计一个集中式控制器，它是主存储器控制器的一部分。其中有一个目录存储在主存储器中，其中包含有关各种本地缓存内容的全局状态信息。当单个CPU Cache 发出读写请求时，这个集中式控制器会检查并发出必要的命令，以在主存和CPU Cache之间或在CPU Cache自身之间进行数据同步和传输。
 

2.Snoopy 协议。这种协议更像是一种数据通知的总线型的技术。CPU Cache通过这个协议可以识别其它Cache上的数据状态。如果有数据共享的话，可以通过广播机制将共享数据的状态通知给其它CPU Cache。这个协议要求每个CPU Cache 都可以“窥探”数据事件的通知并做出相应的反应。

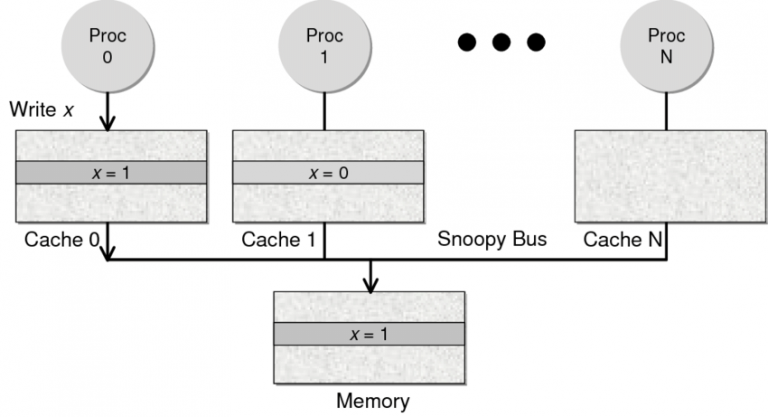
因为Directory协议是一个中心式的，会有性能瓶颈，而且会增加整体设计的复杂度。而Snoopy协议更像是微服务+消息通讯，所以，现在基本都是使用Snoopy的总线的设计。如上图就是Snoopy的总线。

程序实战测试

示例一

首先，假设我们有一个64M长的数组，设想一下下面的两个循环：

const int LEN = 64*1024*1024;
int *arr = new int[LEN];

for (int i = 0; i < LEN; i += 2) arr[i] *= i;

for (int i = 0; i < LEN; i += 8) arr[i] *= i;

按我们的想法来看，第二个循环要比第一个循环少4倍的计算量，其应该也是要快4倍的。但实际跑下来并不是。实际上两个代码跑起来的时间相差无几。这里最主要的原因就是Cache Line，因为CPU会以一个Cache Line 64Bytes最小时单位加载，也就是16个32bits的整型，所以，无论你步长是2还是8，都差不多。而后面的乘法其实是不耗CPU时间的。

示例二

那当我们再以一个固定的步长来访问这个数组呢？

for (int i = 0; i < 10000000; i++) {
    for (int j = 0; j < size; j += increment) {
        memory[j] += j;
    }
}

我们测试一下，在下表中， 表头是步长，也就是每次跳多少个整数，而纵向是这个数组可以跳几次（你可以理解为要几条Cache Line），于是表中的任何一项代表了这个数组有多少，而且步长是多少。比如：横轴是 512，纵轴是4，意思是，这个数组有 4*512 = 2048 个长度，访问时按512步长访问，也就是访问其中的这几项：[0, 512, 1024, 1536] 这四项。

下面是循环1000万次的时间，单位是“微秒”

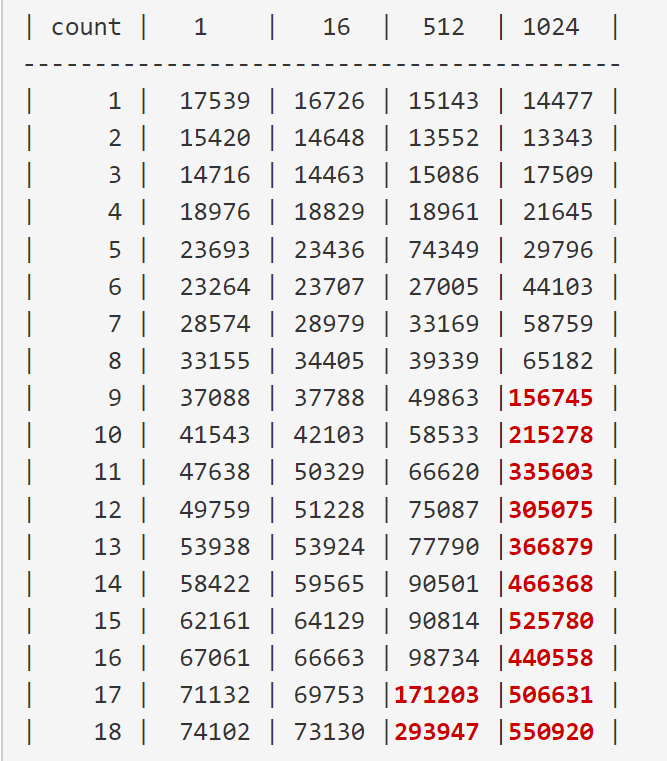
那么我们就能很明显的看到从第九行开始，数值已经开始膨胀起来。

这里就是前面说的地址映射冲突

当步长超过 4096 Bytes（即地址变化 ≥ 12bits）时：

// 示例：步长4096B的内存地址变化模式
0x1000 → 0x2000 → 0x3000...（二进制后12位均为0）
// Set Index计算：
(address >> 6) & 0x3F  // 恒定指向第0组

大家都集中访问第0组 ，导致你这个组内的八个人互相追逐最后撞上了。

这里还涉及中间位冻结效应

在步长512的时候

# 地址增量计算：512×4B=2048 → 二进制0b100000000000
# Set Index位段（bit11-bit6）变化模式：
0b000000 → 0b000001 → ... → 0b000111（仅使用低3位）
# 实际可用组数从64降为8，有效关联度锐减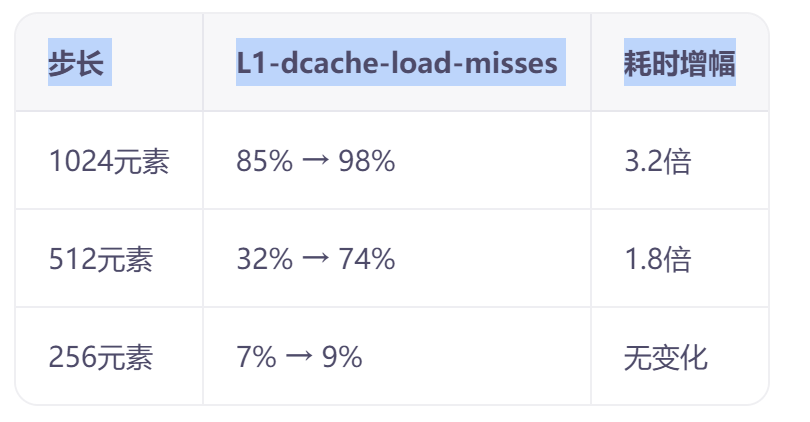

 

那么最后我们就能得出这样的耗时增幅。

好了这篇文章就写到这里，

如果你觉得对你有帮助，可以点赞关注加收藏，感谢您的阅读，我们下一篇文章再见。

一步步来，总会学会的，首先要懂思路，才能有东西写。