线段树

线段树是树状数组的升级版，线段树等于把一个[l,r]的区间，分成很多个小区间，这样方便我们查找一段区间内的信息，不用暴力去跑一遍。

线段树的存储结构：

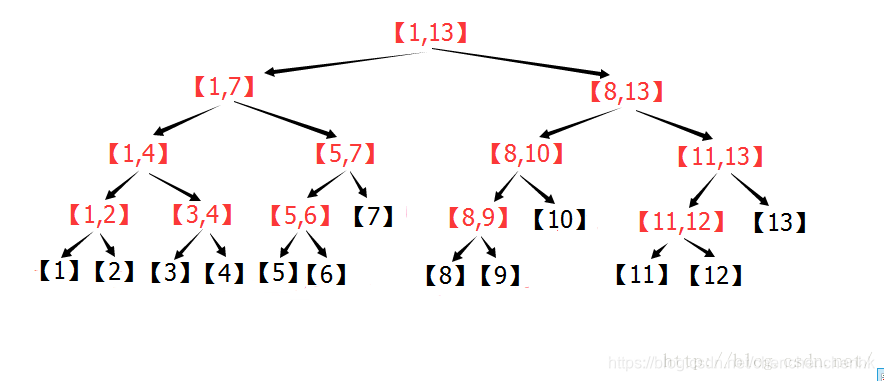
首先是最基本的建树（用的是递归）：
（求一段区间的和）

void pushup(int rt){	// 更新当前结点的值，这里写的是求一段区间的和
    sum[rt] = sum[rt << 1] + sum[r << 1 | 1]; //	当前根的值 = 左子树的值+右子树的值
}

void build(int l, int r, int rt){ // l,r指的是区间，通常是[1,n]，rt是当前区间的下标
    if(l == r){
        sum[rt] = a[l];	//sum数组用来存储当前区间的信息(我们所需要的信息)
        return ;
    }

    int m = (l + r) >> 1;	// 二分，建左子树和右子树
    build(l, m, rt << 1);	// rt << 1 == rt * 2	rt << 1 | 1 == rt * 2 + 1
    build(m+1, r, rt << 1 | 1);
    pushup(rt);	// 这里需要更新当前结点的信息。
}

接下来就是单点修改（通常线段树的题目都会要求你修改某一个点或者修改某一区间所有值）：

void Add(int L, int l, int r, int x,int rt){	//L大区间的左界，l,r是你目前的小区间，x是要求修改的值，rt是当前区间下标
    if(l == r){
        sum[rt] += x;
        return ;
    }

    int m = (l + r) >> 1;
    if(L < m) // 如果m > 大区间左界就要向左子树调用，相反向右子树
    	Add(L, l, m+1, x, rt << 1);
    else
    	Add(L, m+1, l, x, rt << 1 | 1);
    pushup(rt); // 更新当前区间的信息
}

区间修改：

例如一个区间的所有数都+1，你每个数去+1的话就特别慢，线段树的优势就在此处，可以先用一个延迟数组存下这个区间里的数需要+1

void PushDown(int rt,int ln,int rn){	// ln，rn是左子树，右子树数的数量
	if(Add[rt]){	//如果延迟数组表示区间需要改变
		Add[rt<<1]+=Add[rt];	//左右区间继承延迟
		Add[rt<<1|1]+=Add[rt];
		Sum[rt<<1]+=Add[rt]*ln;	//当前区间消除延迟
		Sum[rt<<1|1]+=Add[rt]*rn;
		Add[rt]=0;	//消除延迟
	}
}
void Add(int L,int R,int C,int l,int r,int rt){
	if(L <= l && r <= R){
		Sum[rt]+=C*(r-l+1);
		Add[rt]+=C;
		return ; 
	}
	int m=(l+r)>>1;
	PushDown(rt,m-l+1,r-m);
	if(L <= m) Add(L,R,C,l,m,rt<<1);
	if(R >  m) Add(L,R,C,m+1,r,rt<<1|1); 
	PushUp(rt);
}

最后一步就是查询了：
(区间查询)

int query(int L, int R, int l, int r, int rt){
    if(L <= l && r <= R){
        return sum[rt];
    }

    int m = (l + r) >> 1,ans = 0;
    pushdown(rt);	//还需要消除一下延迟，不然可能错
    if(L >= l)
    	ans += query(L, R, l, m, rt << 1);
    if(R < r)
    	ans += query(L, R, m+1, r, rt << 1 | 1);
    return ans;
}

END