如何对抗GPS欺骗式干扰之二:多天线阵列测向(一)
在GPS欺骗式干扰的产生中我们详细介绍了什么是GPS欺骗式干扰、GPS欺骗式干扰生的特点、生成机制。
在IMU组合导航,抗GPS欺骗式干扰的最有效的方式之一中介绍了IMU组合导航在抗欺骗式干扰中的作用,分析了松组合、紧组合和深组合三种不同模式在融合层次、信息流向,需要的最低卫星个数、抗欺骗能力、实现复杂度等方面的特点。
这次,我们介绍另外一种抗欺骗式干扰的方式:多天线阵列测向方法。
为什么多天线测向能够抗GPS欺骗式干扰?
卫星信号在空间上的特点
GPS接收机接收的是来自于太空中的卫星信号。根据GPS卫星轨道的特点,如果我们以GPS接收机为参考点,那么GPS卫星一定是分布在GPS接收机的不同方向的,而且这些卫星在接收机的视场内均匀分布,不同卫星信号对接收机的到达角度(Angle of Arrival, AOA)相差很大。
而且由于GPS卫星按照特定的轨道运行(大部分导航卫星都是MEO卫星,轨道周期大约是11小时左右)。从地面的GPS接收机的视角来看,卫星的位置随着时间不断变化的,从时间轴上看,卫星信号对于接收机的到达角度也是不断变化的。
下图是GNSS(北斗、GPS)接收机的定位精度计算中给出的GPS卫星和北斗卫星的星图。从图上我们可以看到,GPS卫星、北斗卫星分布在接收机视场内的不同方向(不同的方位角和俯仰角)。
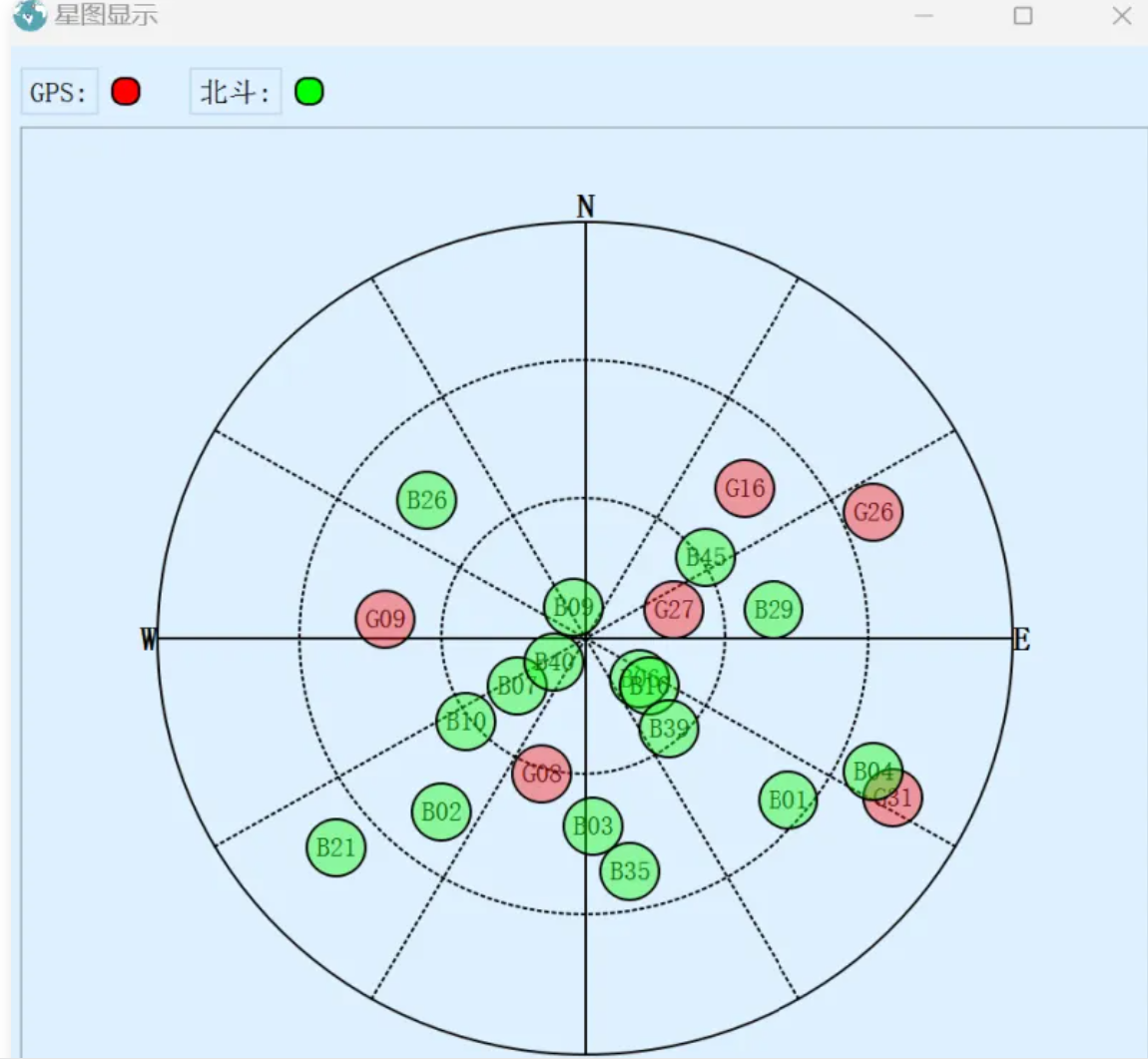
GPS和北斗星图
欺骗式干扰的空间特征
欺骗式干扰通常由一个安装在地面或者临近地面(比如无人机等)的欺骗式干扰发生器生成和发射的。
即使这个欺骗式干扰发生器能够模拟多颗卫星的信号,但是从空间上看,这些伪造的假信号都是从同一个物理点发出的。
因此,所有欺骗信号(无论它们伪装成哪颗卫星)都将从完全相同或极其相似的方向到达接收机天线。
换句话说,欺骗信号在空间上呈现出来自“同一个方向”的高度一致性。对于GPS接收机来说,真实的卫星信号应该是来自于各个不同的方向的,而欺骗式干扰信号却来自于同一个方向或者少数几个方向。
欺骗式干扰在空间上的高度一致性,是多天线测向方法抗欺骗式干扰的基础。
为什么多天线测向能够抗欺骗式干扰
既然欺骗式信号从空间上看,来自于一个或者少数几个方向,那么如果我们能够把每个卫星的到达角计算出来,当我们检测到:大部分卫星信号的到达角度都是同一个方向或者聚焦于某个非常窄的角度区间,那么我们就可以识别出GPS接收机收到的信号是欺骗式信号。
这样一来,识别欺骗式干扰问题就转换成了如何计算每个卫星的到达角的问题。
如何实现多天线测向
多天线测向的核心思路:
-
使用多个天线构成空间阵列;
-
所有天线单元接收同一卫星信号,测量并计算出同一个卫星信号在不同天线单元上的相位差;
-
通过解算的相位差信息,估计每个卫星信号的到达角(方位角 + 俯仰角);
-
分析多颗卫星的到达角分布规律,判断是否存在“异常”的欺骗式信号源。
到达角(Angle of Arrival, AOA)计算的基本原理
到达角(Angle of Arrival, AOA)计算的核心原理:
同一个无线电信号在空间中传播,当它以一定角度到达一个天线阵列时,会因为到达不同的天线单元的路径长度存在差异,在不同的天线单元上产生可测量的相位差(Phase Difference)。根据这个相位差,就可以测量并计算出该无线电信号的到达角(Angle of Arrival, AOA)。
我们先用最简单的模型,2个天线阵列为例,说明如何测量卫星信号的到达角θ。
我们在卫星通信之相控阵天线-极简版中介绍了2个天线阵列的到达角和相位差之间的关系:
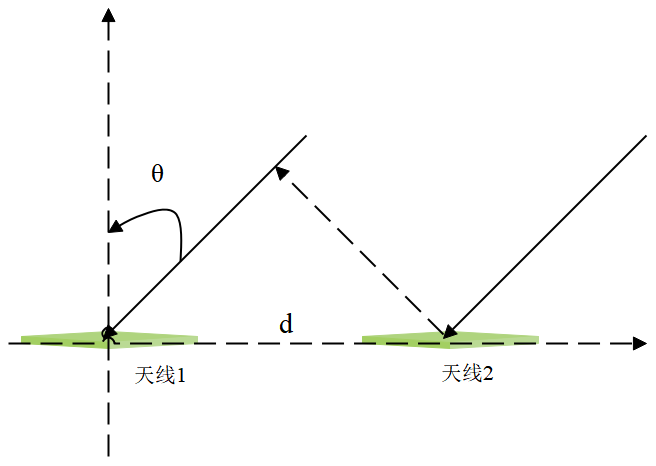
双天线测向

双天线测向2

到达角和相位差之间的关系2
在下面的公式中 △ψ=ψ2−ψ1=2π∗d∗sinθ/λ d:两个天线单元之间的间距;
ψ2和ψ1:分别是天线2的相位、天线1的相位;
θ:是卫星信号的入射方向和天线法向之间的夹角。
λ:卫星信号载波的波长,例如GPS L1频段的载波波长约为19 cm。
在上面的公式中,如果我们把天线1的相位和天线2个相位测量出来,那么就可以计算出到达角θ。 θ=acsin((ψ2−ψ1)∗λ/(2π∗d)
怎么精确测量天线1和天线2的相位并求差
要想精确测量出天线1 的相位和天线2的相位,需要从硬件和软件两方面入手。
射频硬件方面
每个天线对应接收机内部的1个独立的射频通道,射频通道之间必须是“相干”的,必须是“同步”的。这里主要有两点需要注意的:
-
在接收机内部,所有射频通道都使用同一个参考频率源来“下变频”(将高频信号转换为中频或零中频);
-
在模拟信号经过处理后,需要由模数转换器(ADC)进行采样,变成数字信号。所有通道的ADC也必须使用由同一个主时钟源产生的同步采样时钟;
-
所有通道需要采用相同的硬件电路,并保证每个通道的信号延时尽可能的相同。
通过射频硬件层面的处理,我们得到了两路独立的数字中频信号流。虽然信号本身已经变成中频或者基带信号了,但是它们从天线端接收到的原始相位差 ΔΦ 被忠实地保留了下来。
软件/算法方面
软件/算法层面主要是通过载波跟踪环路(PLL锁相环)完成对载波相位的测量。
-
在接收机内部的基带处理器(FPGA或者ASIC)中,为每一个卫星分配2个并行的处理通道。每个通道应独立跟踪同一颗卫星的同一信号,并确保通道间的硬件延迟、滤波器群延迟等系统误差已通过校准消除。
-
通道1:处理来自天线1的信号,其内部的PLL经过跟踪锁定后,输出卫星(PRN=i)的相位测量值 Φ₁。
-
通道2:处理来自天线2的信号,其内部的PLL经过跟踪锁定后,输出卫星(PRN=i)相位测量值 Φ₂。
-
相位差计算:处理器最后执行一个简单的减法,得到相位差 △ψ=ψ2−ψ1
由于两个通道的整个数字处理过程都是在同一个主时钟下进行的,并且使用的本地信号模型也是完全一致的,因此在相减过程中,所有由接收机内部产生的共同延迟和相位偏移都会被抵消掉。最终得到的 ΔΦ 就只剩下由信号到达两个天线物理位置的路径差所造成的部分。
-
计算得到到达角
根据公式计算到达角 由于计算是在FPGA或者ASIC中进行的,必须考虑资源效率、速度和并行性。
-
因为信号波长 λ、天线间距 d 以及 2π 都是常数。因此,整个分母部分 1 / (2π * d) 以及 λ 都可以提前在计算机上计算好,合并成一个固定的常数 K。 K=λ2π∗d
-
把复杂的运算简化为:
X=ΔΦ∗K
-
采用量化、定点的方式计算$ΔΦ*K$;
-
通过查表法,或者CORDIC算法,计算反正弦函数acsin。
如何测量并计算二维方向的到达角
我们上次讨论的双天线模型(天线1和天线2)只能解算信号在一个平面内的到达角,而在三维空间中,我们需要方位角(Azimuth)和俯仰角(Elevation)两个角度来唯一确定一个方向。
要想测量得到卫星信号的入射的方位角和俯仰角,需要2个以上的天线阵列。这里我们以最简单的3天线阵列为例说明。三天线阵列的排列方式如下:
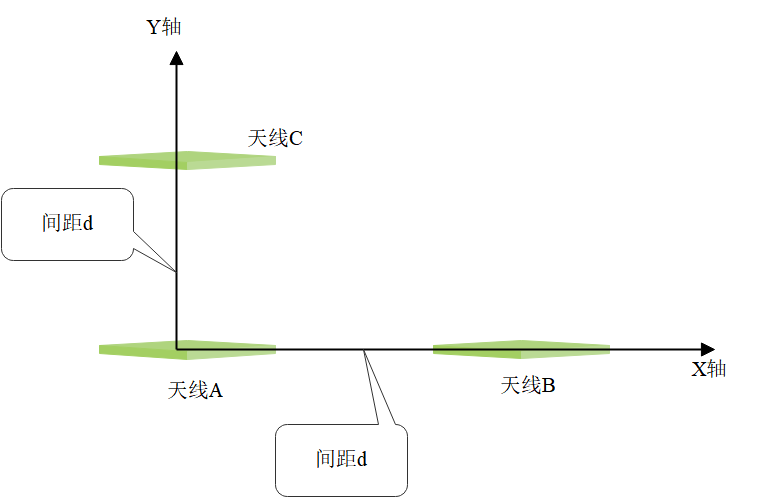
三天线测量到达角
-
三个天线排列成直角L形
-
天线A位于坐标原点:(0, 0, 0)`。
-
天线B在X轴上,坐标为 (d, 0, 0)。
-
天线C在Y轴上,坐标是(0, d, 0)。
我们省略中间的公式推导过程,直接给出结果。
方位角 (Azimuth, φ)定义为: 信号方向在XY平面的投影与X轴(或Y轴,需指明)的夹角,范围0°到360°。
俯仰角 (Elevation, θ):定义为:信号方向与XY平面的夹角,范围0°(地平线)到90°(天顶)。
天线A和天线B之间的相位差是: Δφₓ = (2πd/λ)·cosθ·cosφ
天线A和天线C之间的相位差是:Δφᵧ = (2πd/λ)·cosθ·sinφ
其中俯仰角 θ ,方位角 φ 。
通过联立上面两个方程,得到方位角和俯仰角的计算公式如下:
φ =arctan2(Δφγ,Δφx)
θ=arccos(\frac{λ}{2π*d}\sqrt{Δφ_x^2+Δφ_γ^2}
后续
多天线测向是抗欺骗式干扰的重要手段,那么,
-
计算出到达角之后,根据什么原则判断确实出现了欺骗式干扰
-
当我们用多天线测向发现欺骗式干扰之后,应该采取哪些抑制和消除干扰的措施呢?
-
多天线测向方式有哪些缺点?
-
多天线测向抗欺骗式干扰在哪些场景下会失效?





















 1085
1085

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








