直接偏好优化算法（Direct Preference Optimization，DPO）

DPO

Paper: https://arxiv.org/abs/2305.18290

Code: https://github.com/eric-mitchell/direct-preference-optimization

---

基于 人类反馈的强化学习（RLHF） 是一个复杂且不稳定的过程，首先拟合一个反映人类偏好的奖励模型，然后使用强化学习对大语言模型进行微调，以最大限度地提高估计奖励，同时又不能偏离原始模型太远。这涉及训练多个 LM，并在训练循环中从 LM 采样，从而产生大量的计算成本。

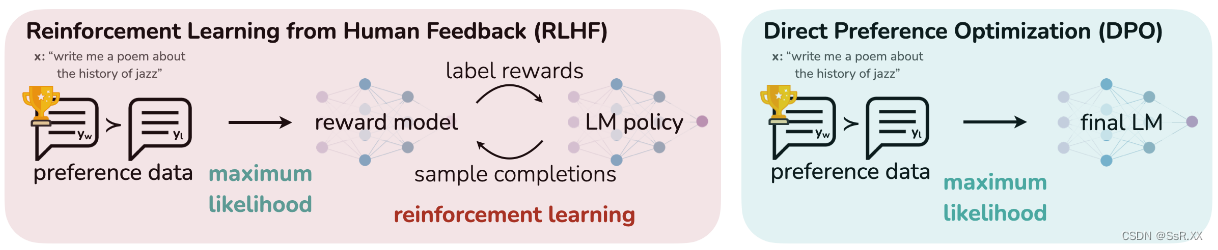
本文作者提出了 直接偏好优化（DPO） 算法，它稳定、高效且计算量轻，无需拟合奖励模型，也无需在微调期间从LM采样或执行显著的超参数调整。实验表明，DPO 可以微调 LMs，使其与人类偏好保持一致，与现有方法一样或更好。值得注意的是，DPO 在情绪控制的能力上超越了 RLHF，提高了总结和单轮对话的响应质量，同时大大简化了实现和训练。

RLHF pipeline

RLHF通常由3个阶段组成：1）监督微调；2）偏好采样和奖励学习；3）强化学习微调；

SFT 阶段

RLHF 通常从一个通用的预训练 LM 开始，该 LM 在高质量数据集上通过监督学习（最大似然）对感兴趣的下游任务（如对话、指令跟随、总结等）进行微调，以获得模型 ${\pi }^{SFT}$。

Reward 建模阶段

在第二阶段，用 $x$ 提示 ${\pi }^{SFT}$ 产生一对答案 $(y_1,y_2)\sim {\pi }^{SFT}(y\mid x)$。通过人类标注，得到偏好标签 $y_w\succ y_l\mid x$，其中 $y_w$ 表示首选补全，$y_l$ 表示非首选补全。

通过静态数据集 D = { x i , y w i , y l i } i = 1 N D=\{x^{i},y^{i}_w,y^{i}_l\}_{i=1}^N D={xi,ywi​,yli​}i=1N​，我们可以将奖励模型 $r_{\varphi }(x,y)$ 参数化，并通过极大似然估计参数。将问题定义为二元分类，我们有负对数似然损失：
$${\mathcal{L}}_R\left(r_{\varphi },\mathcal{D}\right)=-{\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}\left[\log \sigma \left(r_{\varphi }\left(x,y_w\right)-r_{\varphi }\left(x,y_l\right)\right)\right]\text{\hspace{1em}(1)}$$
其中 $\sigma$ 是 $sigmoid$ 函数。奖励模型 $r_{\varphi }(x,y)$ 通常由 ${\pi }^{SFT}$ 进行初始化，并在最后一个 Transformer 层之后添加线性层，该层为奖励值生成单个标量预测。

RL 微调阶段

在 RL 阶段，我们使用学习到的奖励函数来为语言模型提供反馈。特别是，我们制定了以下优化问题：
$$\underset{{\pi }_{\theta }}{\max }{\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(y\mid x)}\left[r_{\varphi }(x,y)\right]-\beta {\mathbb{D}}_{\mathrm{KL}}\left[{\pi }_{\theta }(y\mid x)\Vert {\pi }_{\mathrm{ref}}(y\mid x)\right]\text{\hspace{1em}(2)}$$
其中 $\beta$ 是控制 ${\pi }_{\theta }$ 偏离基本参考策略 ${\pi }_{ref}$ 的参数。在实践中，语言模型策略 ${\pi }_{\theta }$ 也被初始化为 ${\pi }_{ref}$。添加的 $\beta$ 约束很重要，因为它可以防止模型偏离奖励模型准确的分布太远，以及保持生成多样性和防止模式崩溃为单个高奖励答案。由于语言生成的离散性，这个目标是不可微的，并且通常使用强化学习进行优化。标准方法是构造奖励函数 $r(x,y)=r_{\varphi }(x,y)-\beta (\log {\pi }_{\theta }(y\mid x)-\log {\pi }_{ref}(y\mid x))$，并利用 PPO 最大化。

直接偏好优化（DPO）

与之前的 RLHF 方法不同，DPO 绕过了奖励建模步骤，并使用偏好数据直接优化语言模型。

DPO 目标函数

类似于奖励建模方法，即等式 $(1)$，我们的策略目标变为：（推导过程详见原论文）
$${\mathcal{L}}_{\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\mathrm{ref}}\right)=-{\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }\left(y_w\mid x\right)}{{\pi }_{\mathrm{ref}}\left(y_w\mid x\right)}-\beta \log \frac{{\pi }_{\theta }\left(y_l\mid x\right)}{{\pi }_{\mathrm{ref}}\left(y_l\mid x\right)}\right)\right]\text{\hspace{1em}(3)}$$
通过这种方式，我们绕过了显式奖励建模步骤，同时也避免了执行强化学习优化的需要。

逐步分析这个优化目标：首先，$\sigma$ 函数里面的值越大，$L_{DPO}$ 越小。

即最大化 $y_w$ 和 $y_l$ 的奖励函数：
$$\begin{gathered} r_w=\log \frac{{\pi }_{\theta }\left(y_w\mid x\right)}{{\pi }_{\mathrm{ref}}\left(y_w\mid x\right)} \\ {r}_l=\log \frac{{\pi }_{\mathrm{ref}}\left(y_l\mid x\right)}{{\pi }_{\theta }\left(y_l\mid x\right)} \end{gathered}$$
对于人类偏好响应 $y_w$，我们期望 ${\pi }_{\theta }(y_w\mid x)$ 越大越好；

对于人类非偏好响应 $y_l$，我们期望 ${\pi }_{\theta }(y_l\mid x)$ 越小越好。

如果 ${\pi }_{\mathrm{ref}}\left(y_w\mid x\right)$ 比较小，说明参考模型 ${\pi }^{\mathrm{ref}}$ 没有正确分类该偏好响应 $y_w$，此时 $r_w$ 的奖励系数很大。

如果 ${\pi }_{\mathrm{ref}}\left(y_l\mid x\right)$ 比较大，说明参考模型 ${\pi }^{\mathrm{ref}}$ 没有正确分类该非偏好响应 $y_l$，此时 $r_l$ 的奖励系数很大。

DPO outline

1. 对于每个提示 $x$，从参考策略中采样补全 $(y_1,y_2)\sim {\pi }_{\mathrm{ref}}(\cdot \mid x)$，用人类偏好进行标记以构建离线偏好数据集 D = { x i , y w i , y l i } i = 1 N D=\{x^{i},y^{i}_w,y^{i}_l\}_{i=1}^N D={xi,ywi​,yli​}i=1N​。
2. 对于给定的 ${\pi }_{\mathrm{ref}}$、$D$ 和 $\beta$，优化语言模型 ${\pi }_{\theta }$ 以最小化 $L_{\mathrm{DPO}}$。

由于偏好数据集使用 ${\pi }^{SFT}$ 进行采样，因此只要可用，我们就会初始化 ${\pi }_{\mathrm{ref}}={\pi }^{SFT}$。在实践中，人们更愿意重用公开的偏好数据集，而不是生成样本并收集人类偏好。这时我们通过最大化首选补全 $(x,y_w)$ 的似然来初始化 ${\pi }_{\mathrm{ref}}$，即
$${\pi }_{\mathrm{ref}}=\arg {\max }_{\pi }{\mathbb{E}}_{x,y_w\sim \mathcal{D}}\left[\log \pi \left(y_w\mid x\right)\right]$$
该过程有助于缓解真实 ${\pi }_{\mathrm{ref}}$ 与 DPO 使用的 ${\pi }_{\mathrm{ref}}$ 之间的分布偏移。

实验

• 最大化奖励的同时最小化 KL 散度。可以看到 DPO 在保持较小 KL 散度时，也能够达到最大奖励。而 PPO 随着奖励的增大，KL 散度也在增大。
• 对不同采样温度的鲁棒性。DPO 在不同的采样温度下全面优于 PPO，同时在 Best of N 基线的最佳温度下也更胜一筹。

结论

基于人类反馈的强化学习（RLHF）是一个复杂且不稳定的过程，首先拟合一个反映人类偏好的奖励模型，然后使用强化学习对大语言模型进行微调，以最大限度地提高估计奖励，同时又不能偏离原始模型太远。这涉及训练多个 LM，并在训练循环中从 LM 采样，从而产生大量的计算成本。本文作者提出了直接偏好优化（DPO）算法，它稳定、高效且计算量轻，无需拟合奖励模型，也无需在微调期间从LM采样或执行显著的超参数调整。实验表明，DPO 可以微调 LMs，使其与人类偏好保持一致，与现有方法一样或更好。值得注意的是，DPO 在情绪控制的能力上超越了 RLHF，提高了总结和单轮对话的响应质量，同时大大简化了实现和训练。