用于图网络的传统机器学习方法（CS224W课程笔记)

---

前言

这节课讲述了图网络的传统机器学习方法，包括结点级、边级、图级特征的设计。
课程网址：http://web.stanford.edu/class/cs224w/index.html

---

一、结点级特征（Node-level Features）

• 结点的度（Node degree）
• 结点的中心性（Node centrality）
• 聚类系数（Clustering coefficient）
• 非同构子图（Graphlets）

1. 结点的度（Node Degree）

结点 $v$ 的度 $k_v$ 是该节点拥有的边数。

2. 结点的中心性（Node Centrality）

2.1 特征向量中心性（Eigenvector Centrality）

结点v的中心性是其邻居结点u的中心性的总和：
$$c_v=\frac{1}{\lambda }\sum _{u\in N(v)}{c}_u$$
将上述迭代方程写成矩阵的形式：
$$\lambda c=Ac$$
其中，A是邻接矩阵 ，$\lambda$ 取A的最大特征值。

2.2 中介中心性（Betweenness Centrality）

2.3 接近中心性（Closeness Centrality）

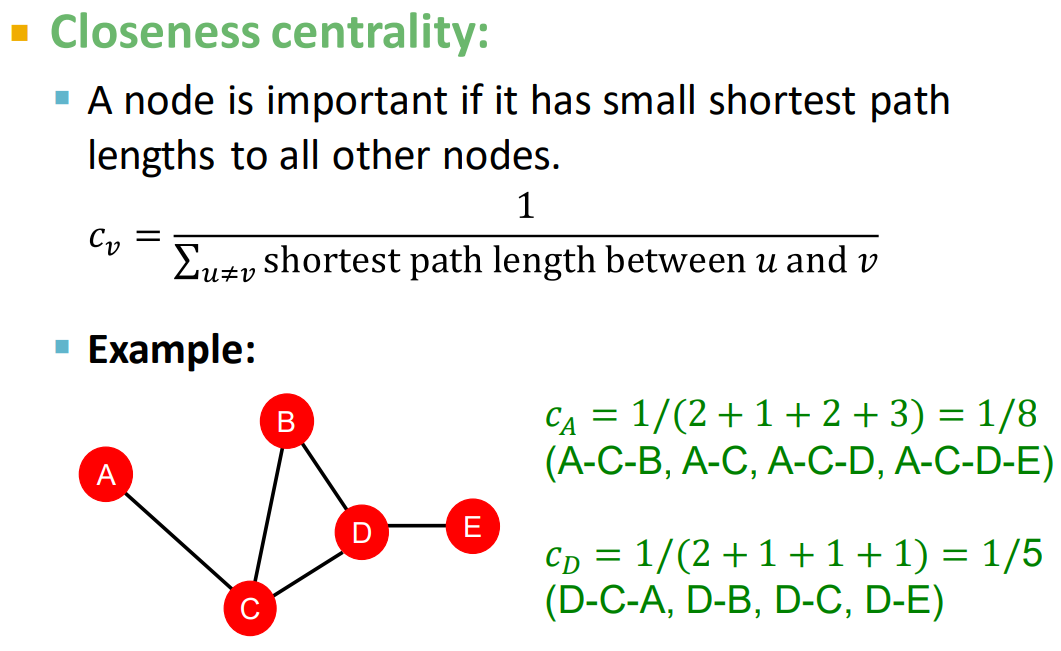
3. 聚类系数（Clustering Coefficient）

本质上就是自我中心网络（ego-network）的三角形的个数

4. 非同构子图（Graphlets）

两个图同构通俗来讲就是：拥有相同数目的结点，并且以相同的方式连接。

n个结点构成的Graphlets的个数随n呈指数增长：

如图，2-node graphlets 有1个，3-node graphlets 有3个，4-node graphlets 有11个，5-node graphlets 有58个。注意：这里的Graphlets要求图是连通的

4.1 Graphlet Degree Vector（GDV）

二、边级特征（Link-level Features）

1. 基于距离的特征（Distance-based Features）

基于两个结点的最短路径距离：

缺点：没有考虑到两个结点的公共邻居个数，例如B和H有2个公共邻居，B和E有1个公共邻居，但是 $S_{BH}=S_{BE}$

2. 局部公共邻居（Local Neighborhood Overlap）

缺点：当两个结点没有公共邻居时，Jaccard’s coefficient 的值为0，但是它们之间仍有可能有边相连。

3. 全局公共邻居（Global Neighborhood Overlap）

Katz Index: count the number of walks of all lengths between a given pair of nodes.
$$S_{v_1{v}_2}=\sum _{l=1}^{\infty }{\beta }^l{A}_{v_1{v}_2}^l$$

计算方法：通过邻接矩阵的k次方 $A^k$ 来计算 $P^{(k)}$

三、图级特征（Graph-level Features）

核方法（kenel method）被广泛用于传统的图级预测。

1. Graphlet kernel

局限性：计算复杂度太高。

2. WL kernel

关于以上两个Graph kernel，详见我的另一篇文章Graph kernel。

---

总结