最小二乘求解非线性曲线拟合（数据拟合）问题-例程

原创于 2024-12-02 17:23:04 发布 · 1.4k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #人工智能

系统辨识以及Matlab相关专栏收录该内容

7 篇文章

订阅专栏

官方

有关基于求解器的求解步骤，包括定义目标函数和约束，以及选择合适的求解器，请参阅基于求解器的优化问题设置。要求解生成的问题，请使用 lsqcurvefit 或 lsqnonlin。

说明

非线性最小二乘求解器-lsqcurvefit，找到求解以下问题的系数 x

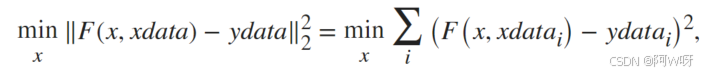
给定输入数据 xdata，观察到的输出 ydata，其中 xdata 和 ydata 是矩阵或向量，F (x, xdata) 是与 ydata 大小相同的矩阵值或向量值函数。

（可选）x 的分量需满足以下约束

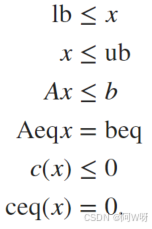
参数 x、lb 和 ub 可以是向量或矩阵；

sqcurvefit函数使用与 lsqnonlin 相同的算法。lsqcurvefit只是为数据拟合问题提供一个方便的接口。lsqcurvefit要求基于用户定义的函数来计算向量值函数，而不是计算平方和。

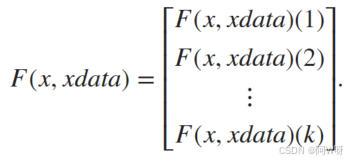
eg:

% 使用lsqcurvefit进行参数辨识
options = optimset('Display', 'off');
[estimated_params, resnorm] = lsqcurvefit(fitting_model, initial_params, v, y, [], [], options);

x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options) 
或 
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,A,b,Aeq,beq,nonlcon,options)

输入参数含义

fun：要拟合的函数，要拟合的函数，指定为函数句柄或函数名称，fun 必须为函数句柄。fun 函数接受两个输入：向量或矩阵 x，以及向量或矩阵 xdata。fun 返回向量或矩阵 F（即在 x 和 xdata 处计算的目标函数值）。
x0：初始点：指定为实数向量或实数数组
xdata：模型的输入数据，指定为实数向量或实数数组。模型是ydata = fun(x,xdata),其中，xdata 和 ydata 是固定数组，x 是 lsqcurvefit 寻求最小平方和时要更改的参数所组成的数组。
resnorm：残差范数的平方，以非负实数形式返回。resnorm是在x 处的残差的2-范数平方：sum((fun(x,xdata)-ydata).^2)。
ydata：模型的响应数据，指定为实数向量或实数数组。
Ib：下界，如果 x0 中的元素数等于 lb 中的元素数，则 lb 指定x(i) >= lb(i)（对于全部 i）。如果 numel(lb) < numel(x0)，则 lb 指定x(i) >= lb(i) (1 <= i <= numel(lb))。如果 lb 的元素数少于 x0，求解器将发出警告。示例： 要指定所有 x 分量为正，请使用 lb = zeros(size(x0))。
ub：上界。
A：线性不等式约束，指定为实矩阵。A 是 M×N 矩阵，其中 M 是不等式的数目，而 N 是变量的数目（x0 中的元素数）。对于大型问题，将 A 作为稀疏矩阵传递。
b：线性不等式约束，指定为实数向量。b 是与 A 矩阵相关的包含 M 个元素的向量。如果将 b 作为行向量传递，求解器会在内部将 b 转换为列向量 b(:)。对于大型问题，将 b 作为稀疏向量传递。
Aeq：线性等式约束，Aeq 是 Me×N 矩阵，其中 Me 是等式的数目，而 N 是变量的数目（x0 中的元素数）。对于大型问题，将 Aeq 作为稀疏矩阵传递。
beq：线性等式约束，beq 是与 Aeq 矩阵相关的包含 Me 个元素的向量。如果将 beq 作为行向量传递，求解器会在内部将 beq 转换为列向量 beq(:)。对于大型问题，将 beq 作为稀疏向量传递。
nolcon：非线性约束，非线性约束，指定为函数句柄。nonlcon 函数接受向量或数组 x，并返回两个数组 c(x) 和 ceq(x)。c(x) 是由 x 处的非线性不等式约束组成的数组。lsqcurvefit 尝试满足：对于 c 的所有项，有 c(x) <= 0。ceq(x) 是由 x 处的非线性等式约束组成的数组。lsqcurvefit 尝试满足：对于 ceq 的所有项，有 ceq(x) = 0。
options：优化选项，指定为 optimoptions 的输出或 optimset 等返回的结构体。

输出参数含义

x：解，以实数向量或实数数组形式返回。x 的大小与 x0 的大小相同。通常情况下，当 exitflag 为正时，x 是该问题的局部解。有关解质量的信息，请参阅求解成功后。
resnorm：残差范数的平方，以非负实数形式返回。resnorm 是在 x 处的残差的 2-范数平方：sum((fun(x,xdata)-ydata).^2)。
residual：在解处的目标函数值，以数组形式返回。一般来说，residual = fun(x,xdata)-ydata。
exitflag — 求解器停止的原因。
output — 有关优化过程的信息。
lambda — 解处的拉格朗日乘数。
jacobian — 解处的雅可比矩阵

替代功能

App优化实时编辑器任务为 lsqcurvefit 提供可视化界面

代码

% 假设你已经有了输入v和输出y的数据
v = double([your_input_data_here]); % 确保v是双精度类型
y = double([your_output_data_here]); % 确保y是双精度类型

% 模型方程，这里需要你根据实际模型来定义
% 例如：y_pred = p1 * exp(-p2 * v) + p3;
fitting_model = @(p, v) p(1) * exp(-p(2) * v) + p(3);

% 初始参数猜测值
initial_params = [1, 0.1, 1];

% 使用lsqcurvefit进行参数辨识
options = optimset('Display', 'off');
[estimated_params, resnorm] = lsqcurvefit(fitting_model, initial_params, v, y, [], [], options);

% 显示辨识出的参数
disp('辨识出的参数为:');
disp(estimated_params);

% 使用辨识出的参数计算模型预测输出
y_pred = fitting_model(estimated_params, v);

% 计算并显示误差
error = sum((y - y_pred).^2);
disp(['误差平方和为: ', num2str(error)]);

% 绘制实际输出与模型预测输出的对比图
figure;
plot(v, y, 'bo', 'MarkerSize', 5); hold on;
plot(v, y_pred, 'r-', 'LineWidth', 2);
xlabel('输入 v');
ylabel('输出 y');
legend('实际输出', '模型预测');
title('模型拟合');
grid on;

举例

、

自己编写代码

%% 递推最小二乘法辨识参数
% 辨识参数个数：n个
lambda = 1; % 遗忘因子  
thetae_1 = zeros(n,1); % 权重估计初值  
P = 10^6 * eye(n); % 初始协方差矩阵
xi=sqrt(0.01)*randn(N,1); %白噪声序列

for k = 1:N
    phi=Fr(:, k);
    y(k)=y_ture(k);
    %递推最小二乘法
    K=P*phi/(lambda+phi'*P*phi);
    thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);
    P=(eye(n)-(1/lambda)*K*phi')*P;
    %更新输入数据
    thetae_1=thetae(:,k);
end
% 输出最后迭代得到的参数值theta即权重w1-wn
for i = 1:n
    fprintf('w%d: %.4f\n', i, thetae_1(i));
end