编译原理第三版陈火旺第二章答案

钻仰弥坚

已于 2024-03-20 11:08:01 修改

阅读量1.4w

点赞数 67

CC 4.0 BY-SA版权

分类专栏：编译原理文章标签： c语言编译原理

于 2022-10-18 00:06:25 首次发布

本文链接：https://blog.youkuaiyun.com/capture3333/article/details/127344613

编译原理专栏收录该内容

9 篇文章

订阅专栏

本文探讨了程序设计语言中的标识符和名字的区别，以及表达式的计算规则。此外，还涉及文法规则的解析，包括最左推导和最右推导，并展示了如何构造无二义文法。同时，文章通过具体例子说明了文法的二义性，并给出了消除二义性的方法。最后，讨论了如何生成特定语言的文法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

下面答案仅供参考！

3.何谓“标识符”，何谓“名字”，两者的区别是什么？

答：在程序设计语言中，标识符是一个最基本的概念，其定义为：凡以字母开头的字母数字序列（有限个字符）都是标识符。当给予某标识符以确切的含义时，这个标识符就叫做名字。程序语言中各种名字都是用标识符表示的，只是标识符是一个没有意义的字符序列，而名字却有着确切的意义和属性（即类型和作用域）。如当A、B1等作为标识符时没有什么含义，但当其作为名字时，却可以代表变量名、数组名、函数名或过程名等。

4、令＋、* 和↑代表加、乘和乘幂，按如下的非标准优先级和结合性质的约定，计算1＋1*2↑*1↑2的值：

(1) 优先顺序（从高至低）为＋、* 和↑，同级优先采用左结合。

(2）优先顺序为↑、＋、*，同级优先采用右结合。

答:（1）1＋1*2↑*1↑2 = 2*2↑*1↑2 = 4↑*1↑2 = 4↑↑2 =

（2）1＋1*2↑*1↑2 =

6.令文法G6为

N→D∣ND

D→0∣1∣2∣3∣4∣5∣6∣7∣8∣9

(1) G6 的语言 L(G6)是什么？

(2) 给出句子 0127、34 和 568 的最左推导和最右推导。

7.写一个文法，使其语言是奇数集，且每个奇数不以0开头。

答：首先分析题意，本题是希望构造一个文法，由它产生的句子是奇数，并且不以 0 开头，也就是说它的每个句子都是以 1、3、5、7、9中的某个数结尾。如果数字只有一位，则满足要求，如果有多位，则要求第 1 位不能是0,而中间有多少位，每位是什么数字(必须是数字)则没什么要求，因此，我们可以把这个文法分 3 部分来完成。分别用3个非终结符来产生句子的第 1 位、中间部分和最后 1 位。引入几个非终结符，其中，一个用作产生句子的开头，可以是 1 ~ 9之间的数，不包括 0,一个用来产生句子的结尾，为奇数，另一个则用来产生以非 0整数开头后面跟任意多个数字的数字串，进行分解之后，这个文法就很好写了。

G(S)：A→2∣4∣6∣8∣D

B→A∣0

C→CB∣A

D→1∣3∣5∣7∣9

S→CD∣D

8.令文法为

E→T∣E+ T∣E-T

T→F∣T*F∣T/F

F→(E)∣i

（1）给出 i*(i+ i)的最左推导和最右推导

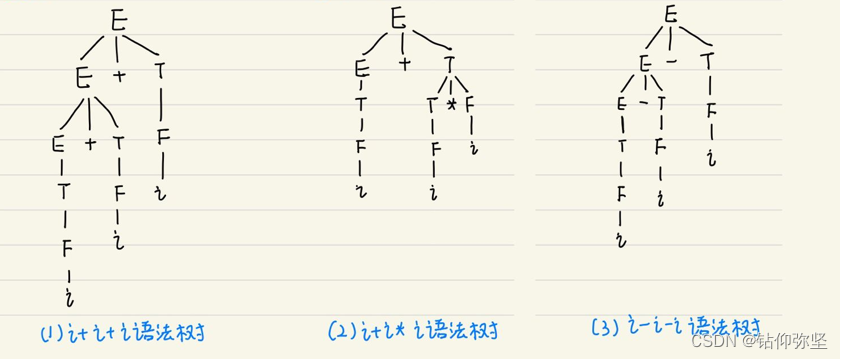
（2）给出 i+ i+i 以 i+i *i 和 i-i-i 的语法树。

9.证明下面的文法是二义的：

S→iSeS∣iS∣i

答：根据文法的二义性的定义，如果要证明该文法是二义的，必须找到一个句子，使得该句子具有两个不同的最右推导或两个不同的语法树。我们首先分析这个文法，根据我们对程序语言的了解，不难发现，这个文法应该是用来表示 if...else…结构的(用“i”代表“if” 或语句集，“e”代表“else”)。因此我们就要到if...else…结构中去找二义性。我们知道，程序语言一般都规定else部分是和它前面离它最近的没有被匹配的if语句进行匹配。而上面的这个文法体现不出这种限制，因此我们可以找这样一个句子,在else前面有两个if(如句子 iiiei), else和不同的if进行匹配时就会产生不同的语义。

考虑句子iiiei,存在如下两个最右推导:

由此该文法是二义的。

10.把下面文法改写为无二义的:

S -> SSI(S)I( )

答：本题给出的文法是二义的，关键在于 S -> SS 是产生二义的根源，我们将该产生式改造成等价的递归结构，消除二义性。

产生式S -> SS 意味着一个符号串可以被多次重复，并且这个重复过程是递归的，因此在推导的过程中会有多种可能的解释方式。这种重复导致了二义性，为了消除这种二义性，可以对文法进行改写，引入一个新的非终结符，将产生式 S -> SS 分解成多个产生式，使得推导过程无二义性。

将文法改造成 G(S)：

S-> TS I T

T-> (S) I ( )

11 . 给出下面语言的相应文法

$\begin{array}{c}\mathbf{L_1}=\{\mathbf{a^nb^nc^i}\mid\mathbf{n\geq1},\mathbf{i\geq0}\}\\ \mathbf{L_2}=\{\mathbf{a^ib^nc^n}\mid\mathbf{n\geq1},\mathbf{i\geq0}\}\\ \mathbf{L_3}=\{\mathbf{a^nb^n}\mathbf{a^mb^m}\mid\mathbf{n,m\geq0}\}\\ \mathbf{L_4}=\{\mathbf{1^n0^m1^m0^n}\mid\mathbf{n,m\geq0}\}\end{array}$