【python】基于MCC（最大相关熵）的卡尔曼滤波的python代码，一维滤波，应对观测数据突变，附下载链接

本代码实现了**最大相关熵卡尔曼滤波（MCC-KF）**与经典卡尔曼滤波（KF）的对比仿真，重点验证MCC-KF在存在异常观测值场景下的鲁棒性改进。通过高斯核函数动态加权残差，MCC-KF能有效抑制异常值对状态估计的影响。

运行结果

状态曲线：

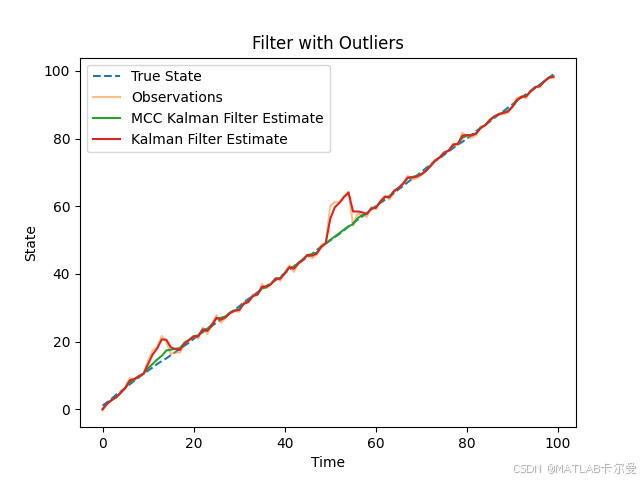
误差曲线：

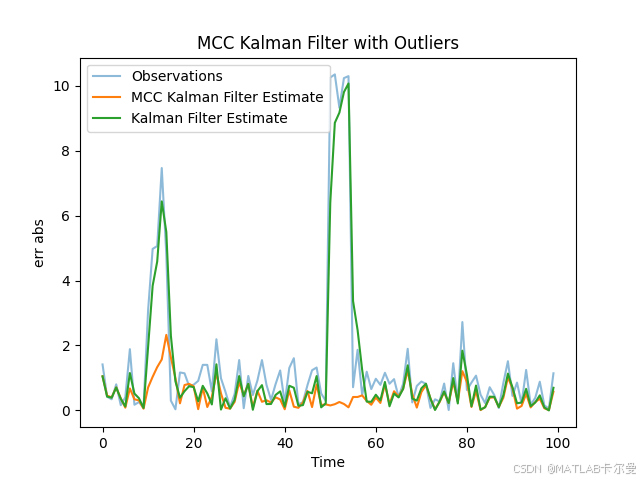
Python源代码

以下代码复制粘贴到空脚本中即可直接运行：

import numpy as np

# 高斯核函数
def gaussian_kernel(x, sigma):
    return np.exp(-x**2 / (2 * sigma**2))

# MCC 卡尔曼滤波
def mcc_kalman_filter(z, F, H, Q, R, x0, P0, sigma):
    """
    参数：
    z: 观测值序列 (numpy array, shape = [T, 1])
    F: 状态转移矩阵 (numpy array, shape = [n, n])
    H: 观测矩阵 (numpy array, shape = [m, n])
    Q: 过程噪声协方差矩阵 (numpy array, shape = [n, n])
    R: 观测噪声协方差矩阵 (numpy array, shape = [m, m])
    x0: 初始状态估计 (numpy array, shape = [n, 1])
    P0: 初始协方差矩阵 (numpy array, shape = [n, n])
    sigma: MCC 高斯核的带宽参数

    返回：
    x_est_MCC: 估计的状态序列 (numpy array, shape = [T, n])
    """
    # 初始化
    T = len(z)       # 时间序列长度
    n = x0.shape[0]  # 状态维度
    x_est_MCC = np.zeros((T, n, 1))  # 保存状态估计
    x_est_MCC[0] = x0
    P = P0

    for t in range(1, T):
        # 预测
        x_pred = F @ x_est_MCC[t - 1] +1 # 预测状态
        P_pred = F @ P @ F.T + Q         # 预测协方差

        # 计算残差
        y = z[t] - H @ x_pred

        # MCC 权重
        w = gaussian_kernel(y, sigma)

        # 卡尔曼增益（基于 MCC）
        S = H @ P_pred @ H.T + R
        K = P_pred @ H.T @ np.linalg.inv(S)

        # 更新状态与协方差
        x_est_MCC[t] = x_pred + K @ (w * y)
        P = P_pred - K @ H @ P_pred

    return x_est_MCC


# 经典卡尔曼滤波
def kalman_filter(z, F, H, Q, R, x0, P0, sigma):
    """
    参数：
    z: 观测值序列 (numpy array, shape = [T, 1])
    F: 状态转移矩阵 (numpy array, shape = [n, n])
    H: 观测矩阵 (numpy array, shape = [m, n])
    Q: 过程噪声协方差矩阵 (numpy array, shape = [n, n])
    R: 观测噪声协方差矩阵 (numpy array, shape = [m, m])
    x0: 初始状态估计 (numpy array, shape = [n, 1])
    P0: 初始协方差矩阵 (numpy array, shape = [n, n])
    sigma: MCC 高斯核的带宽参数

    返回：
    x_est_KF: 估计的状态序列 (numpy array, shape = [T, n])
    """
    # 初始化
    T = len(z)       # 时间序列长度
    n = x0.shape[0]  # 状态维度
    x_est_KF = np.zeros((T, n, 1))  # 保存状态估计
    x_est_KF[0] = x0
    P = P0

    for t in range(1, T):
        # 预测
        x_pred = F @ x_est_KF[t - 1] +1 # 预测状态
        P_pred = F @ P @ F.T + Q         # 预测协方差

        # 计算残差
        y = z[t] - H @ x_pred

        # MCC 权重
        w = gaussian_kernel(y, sigma)

        # 卡尔曼增益（基于 MCC）

完整代码的下载链接：https://download.youkuaiyun.com/download/callmeup/90958788

核心算法原理

最大相关熵准则（MCC）

基于信息论中的熵最大化原则，通过高斯核函数赋予残差自适应权重：
$$w=\exp \left(-\frac{e^2}{2{\sigma }^2}\right)$$
其中$e$为观测残差，$\sigma$为核带宽参数。异常值对应的残差较大时权重降低，从而抑制其影响。

MCC-KF 改进步骤

• 预测环节：与经典KF相同，通过状态转移矩阵 (F) 预测状态和协方差
• 更新环节：引入高斯核函数修正卡尔曼增益，更新公式调整为：
  $${\hat{x}}_t=x_{\text{pred}}+K\cdot (w\cdot y)$$
  相较经典KF的$K\cdot y$，$w$作为附加权重压缩异常值。

代码模块解析

高斯核函数

计算残差的权重，核带宽$\sigma$控制对异常值的敏感度。

MCC-KF 实现

def mcc_kalman_filter(z, F, H, Q, R, x0, P0, sigma):
    # 核心循环
    for t in range(1, T):
        # 预测步骤（同经典KF）
        y = z[t] - H @ x_pred
        w = gaussian_kernel(y, sigma)  # 计算权重
        x_est_MCC[t] = x_pred + K @ (w * y)  # 加权更新

在残差更新环节引入权重 (w)，抑制大残差值的影响。

测试数据生成

构造含两段显著异常值的观测序列，测试算法鲁棒性。

改进方向

1. 动态核带宽：根据残差统计特性自适应调整 (\sigma)
2. 多核函数扩展：使用混合核（如拉普拉斯核）提升复杂噪声适应性
3. 工程优化：矩阵运算加速（如Cholesky分解替代直接求逆）

总结

本代码通过对比验证了MCC-KF在异常值场景下的优越性，可作为传感器信号处理、组合导航等领域的鲁棒滤波算法基础框架。实际应用中需结合具体噪声特性调整核参数与系统模型。

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者