【课题推荐】使用EKF融合加速度计和陀螺仪数据估计坡度角的方法

前面说到了基于GPS的坡度估计仿真（附源代码）https://blog.youkuaiyun.com/callmeup/article/details/146196150，这里给出使用EKF融合加速度计和陀螺仪数据估计坡度角的方法

系统建模

状态变量

选择坡度角θ和陀螺仪偏差b作为状态变量：
$$\mathbf{x}=\left[\begin{array}{c}\theta \\ b\end{array}\right]$$

状态方程（过程模型）

• 陀螺仪测量的角速度ω包含偏差b，离散时间步长为Δt：
  $${\theta }_{k+1}={\theta }_k+({\omega }_k-b_k)\cdot \Delta t+w_{\theta }$$
  $$b_{k+1}=b_k+w_b$$
  其中，$w_{\theta }$和$w_b$为过程噪声，假设为高斯白噪声。

• 矩阵形式：
  $${\mathbf{x}}_{k+1}=\mathbf{F}{\mathbf{x}}_k+\mathbf{w}$$
  状态转移矩阵：
  $$\mathbf{F}=\left[\begin{array}{cc}1& -\Delta t\\ 0& 1\end{array}\right]$$
  过程噪声协方差矩阵：
  $$\mathbf{Q}=\left[\begin{array}{cc}{\sigma }_{\theta }^2& 0\\ 0& {\sigma }_b^2\end{array}\right]$$

观测模型

加速度计观测方程

加速度计测量值包含车辆纵向加速度$a_{\text{vehicle}}$和重力分量：
$$z_k=a_{\text{vehicle}}+g\sin {\theta }_k+v_k$$
其中，$v_k$为观测噪声，假设为高斯白噪声。

观测矩阵（非线性）

观测函数为：
$$h({\mathbf{x}}_k)=a_{\text{vehicle}}+g\sin {\theta }_k$$
雅可比矩阵（用于EKF线性化）：
$${\mathbf{H}}_k=\left[\begin{array}{cc}g\cos {\theta }_k& 0\end{array}\right]$$
观测噪声协方差：
$$R={\sigma }_z^2$$

扩展卡尔曼滤波（EKF）流程

初始化

设置初始状态和协方差：
$${\hat{\mathbf{x}}}_0=\left[\begin{array}{c}0\\ 0\end{array}\right],{\mathbf{P}}_0=\text{diag}(p_{\theta },p_b)$$

预测步骤

1. 预测状态：
   $${\hat{\mathbf{x}}}_{k|k-1}=\mathbf{F}{\hat{\mathbf{x}}}_{k-1}$$
2. 预测协方差：
   $${\mathbf{P}}_{k|k-1}=\mathbf{F}{\mathbf{P}}_{k-1}{\mathbf{F}}^T+\mathbf{Q}$$

更新步骤

1. 计算卡尔曼增益：
   $${\mathbf{K}}_k={\mathbf{P}}_{k|k-1}{\mathbf{H}}_k^T{\left({\mathbf{H}}_k{\mathbf{P}}_{k|k-1}{\mathbf{H}}_k^T+R\right)}^{-1}$$
2. 更新状态估计：
   $${\hat{\mathbf{x}}}_k={\hat{\mathbf{x}}}_{k|k-1}+{\mathbf{K}}_k\left(z_k-h({\hat{\mathbf{x}}}_{k|k-1})\right)$$
3. 更新协方差：
   $${\mathbf{P}}_k=(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k){\mathbf{P}}_{k|k-1}$$

关键实现细节

• 车辆加速度获取：假设通过车辆CAN总线或轮速传感器微分获得$a_{\text{vehicle}}$，否则需联合估计。
• 非线性处理：使用EKF或UKF处理观测模型中的$\sin \theta$。
• 噪声调整：根据传感器特性调整$\mathbf{Q}$和$R$，如陀螺仪噪声大则增大${\sigma }_{\theta }^2$。
• 初始条件：静止时可初始化θ为加速度计计算值，提高收敛速度。

公式总结

• 状态预测：
  $${\theta }_{k|k-1}={\theta }_{k-1}+({\omega }_{k-1}-b_{k-1})\Delta t$$
  $$b_{k|k-1}=b_{k-1}$$

• 观测更新：
  $${\theta }_k={\theta }_{k|k-1}+K_{\theta }\left(\frac{z_k-a_{\text{vehicle}}}{g}-\sin {\theta }_{k|k-1}\right)$$
  $$b_k=b_{k|k-1}+K_b\left(\frac{z_k-a_{\text{vehicle}}}{g}-\sin {\theta }_{k|k-1}\right)$$

参数调试建议

• 通过Allan方差分析陀螺仪噪声，确定过程噪声参数。
• 静态测试标定加速度计噪声。
• 使用斜坡道路实测数据验证坡度估计精度。

MATLAB代码

部分源代码

%% 车辆坡度估计EKF仿真，使用EKF融合加速度计和陀螺仪数据估计坡度角
% 作者：matlabfilter

clear; clc; close all;

%% 1. 参数设置
dt = 0.01;          % 采样时间(s)
T = 10;             % 总时长(s)
N = T/dt;           % 数据点数
g = 9.81;           % 重力加速度(m/s²)

% 过程噪声协方差矩阵Q
Q = diag([0.001, 0.0001]);  % 角度和偏差的噪声

% 观测噪声协方差R
R = 0.1;            % 加速度计噪声

% 传感器特性
gyro_bias = 0.1;    % 陀螺仪固定偏差(rad/s)
gyro_noise = 0.01;  % 陀螺仪噪声强度
accel_noise = 0.1;  % 加速度计噪声强度

%% 2. 生成真实数据
% 真实坡度角（示例：斜坡+正弦变化）
true_theta = linspace(0, 0.5, N) + 0.1*sin(2*pi*(0:N-1)/N);
true_bias = gyro_bias*ones(1,N); 

% 真实角速度（坡度角导数 + 偏差）
true_omega = diff(true_theta)/dt + gyro_bias;
true_omega = [true_omega, true_omega(end)];

% 车辆纵向加速度（示例：正弦变化）
a_vehicle = 0.5*sin(2*pi*(0:N-1)/N);

% 生成传感器数据
gyro_meas = true_omega + gyro_noise*randn(1,N);  % 陀螺仪测量值
accel_meas = a_vehicle + g*sin(true_theta) + accel_noise*randn(1,N); % 加速度计测量值

%% 3. EKF初始化


%% 4. EKF主循环


%% 5. 结果可视化

运行结果

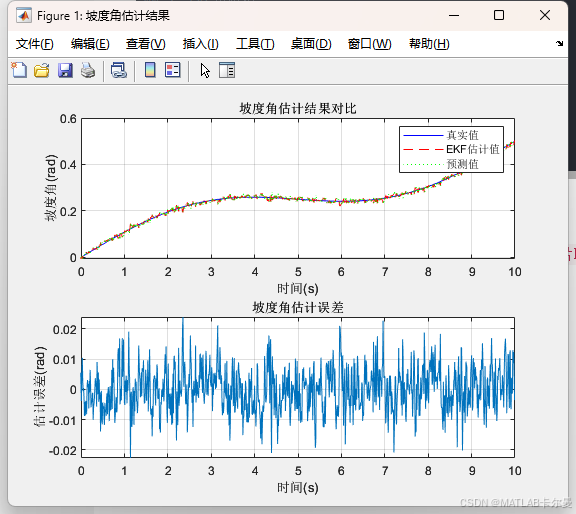
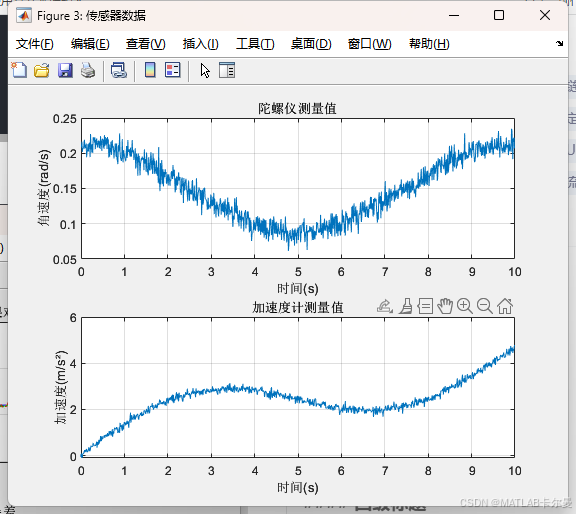
如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者