CodeForces 689D Friends and Subsequences （RMQ+二分）

最新推荐文章于 2024-12-01 03:34:23 发布

c_cl

最新推荐文章于 2024-12-01 03:34:23 发布

阅读量176

点赞数

CC 4.0 BY-SA版权

分类专栏：思维

本文链接：https://blog.youkuaiyun.com/c_czl/article/details/81137290

思维专栏收录该内容

67 篇文章

订阅专栏

本文介绍了一种解决特定RMQ（Range Maximum Query）与RMI（Range Minimum Query）问题的方法，通过对两个序列进行预处理，实现O(nlogn)的时间复杂度，并在O(1)时间内回答每个查询。通过二分查找确定区间左右边界，最终计算出满足条件的区间数量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题面：

D. Friends and Subsequences

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?

Every one of them has an integer sequences a andb of length n. Being given a query of the form of pair of integers(l, r), Mike can instantly tell the value of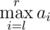 while !Mike can instantly tell the value of.

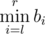Now suppose a robot (you!) asks them all possible different queries of pairs of integers(l, r) (1 ≤ l ≤ r ≤ n) (so he will make exactlyn(n + 1) / 2 queries) and counts how many times their answers coincide, thus for how many pairs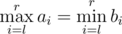 is satisfied.

How many occasions will the robot count?

Input

The first line contains only integer n (1 ≤ n ≤ 200 000).

The second line contains n integer numbersa1, a2, ..., an ( - 109 ≤ ai ≤ 109) — the sequence a.

The third line contains n integer numbersb1, b2, ..., bn ( - 109 ≤ bi ≤ 109) — the sequence b.

Output

Print the only integer number — the number of occasions the robot will count, thus for how many pairs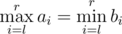 is satisfied.

Examples

Input

6
1 2 3 2 1 4
6 7 1 2 3 2

Output

Input

3
3 3 3
1 1 1

Output

Note

The occasions in the first sample case are:

1.l = 4,r = 4 sincemax{2} = min{2}.

2.l = 4,r = 5 sincemax{2, 1} = min{2, 3}.

There are no occasions in the second sample case since Mike will answer 3 to any query pair, but !Mike will always answer 1.

题意：

给定两个等长区间，求相同l,r情况下，有多少个区间，第一个序列的最大值和第二个序列的最小值相同。

解题：

RMQ，O（nlog（n））的复杂度，随后可以做到O（1）询问。但若枚举区间l，r，复杂度仍为O(n^2)。这时可以利用区间特性进行二分，固定区间左端点（注意区间左端点和二分左端点不一样），若二分右端点所在位置形成的最小值不等于最大值，若最小值大于最大值，说明仍可以右移，还有希望相等。若最小值小于最大值，则说明区间过长，左移区间左端点。若相等，则根据当前是求右边界最左端还是最右端进行相应移动。

此题比较特殊的是，枚举左区间端点，但左区间端点和左二分端点是不一样的，二分的是区间右端点。每次通过两次二分，求出每一区间左端点对应的区间右端点的两个位置极值，作差，求和，求得结果。

/*
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<map>

using namespace std;

int n;
int a[200005];
int b[200005];

int ma[200005][25];
int mi[200005][25];

void cal()
{
    for(int i=0;i<n;i++)
    {
        ma[i][0]=a[i];
        mi[i][0]=b[i];
    }


    for(int j=1;(1<<j)<=n;j++)
    {
        for(int i=0;i+(1<<j)<=n;i++)
        {
            ma[i][j]=max(ma[i][j-1],ma[i+(1<<(j-1))][j-1]);
            mi[i][j]=min(mi[i][j-1],mi[i+(1<<(j-1))][j-1]);
        }
    }
}

int gma(int l,int r)
{
    int k=0;
    while((1<<(k+1))<=(r-l+1))
        k++;

    return max(ma[l][k],ma[r-(1<<k)+1][k]);
}

int gmi(int l,int r)
{
    int k=0;
    while((1<<(k+1))<=(r-l+1))
        k++;

    return min(mi[l][k],mi[r-(1<<k)+1][k]);
}

int bins(int sta)
{
    int l=sta,r=n-1;
    int maxn,minn;
    while(l<r)
    {
        int mid=(l+r)/2;
        maxn=gma(sta,mid);
        minn=gmi(sta,mid);

        if(maxn>minn)
        {
            r=mid-1;
        }
        else if(maxn<minn)
        {
            l=mid+1;
        }
        else if(maxn==minn)
        {
            r=mid;
        }
    }
    if(l==r && gma(sta,l)==gmi(sta,r))
        return l;
    else
        return -1;

}

int bine(int sta)
{
    int l=sta,r=n-1;
    int maxn,minn;
    while(l<r)
    {
        int mid=(l+r)/2;
        maxn=gma(sta,mid);
        minn=gmi(sta,mid);

        if(maxn>minn)
        {
            r=mid-1;
        }
        else if(maxn<minn)
        {
            l=mid+1;
        }
        else if(maxn==minn)
        {
            l=mid;
        }

        if((l+1)==r)
        {
            if(gma(sta,r)==gmi(sta,r))
                return r;
            if(gma(sta,l)==gmi(sta,l))
                return l;

            return -1;
        }
    }
    if(l==r && gma(sta,l)==gmi(sta,r))
        return l;
    else
        return -1;

}

int main()
{
    while(~scanf("%d",&n))
    {
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        for(int i=0;i<n;i++)
            scanf("%d",&b[i]);

        cal();

        long long ans=0;
        for(int i=0;i<n;i++)
        {
            int s=bins(i);
            int e=bine(i);

            //printf("%d : %d %d\n",i,s,e);
            if(s!=-1 && e!=-1)
            {
                ans+=(e-s+1);
            }
        }
        printf("%lld\n",ans);
    }

}
*/

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<map>

using namespace std;

int n;
int a[200005];
int b[200005];

int ma[200005][25];
int mi[200005][25];

void cal()
{
    for(int i=0;i<n;i++)
    {
        ma[i][0]=a[i];
        mi[i][0]=b[i];
    }


    for(int j=1;(1<<j)<=n;j++)
    {
        for(int i=0;i+(1<<j)<=n;i++)
        {
            ma[i][j]=max(ma[i][j-1],ma[i+(1<<(j-1))][j-1]);
            mi[i][j]=min(mi[i][j-1],mi[i+(1<<(j-1))][j-1]);
        }
    }
}

int gma(int l,int r)
{
    int k=0;
    while((1<<(k+1))<=(r-l+1))
        k++;

    return max(ma[l][k],ma[r-(1<<k)+1][k]);
}

int gmi(int l,int r)
{
    int k=0;
    while((1<<(k+1))<=(r-l+1))
        k++;

    return min(mi[l][k],mi[r-(1<<k)+1][k]);
}

int bins(int sta)
{
    int l=sta,r=n-1;
    int maxn,minn;
    int ans=-1;
    while(l<=r)
    {
        int mid=(l+r)/2;
        maxn=gma(sta,mid);
        minn=gmi(sta,mid);

        if(maxn>minn)
        {
            r=mid-1;
        }
        else if(maxn<minn)
        {
            l=mid+1;
        }
        else if(maxn==minn)
        {
            r=mid-1;
            ans=mid;
        }
    }
    return ans;

}

int bine(int sta)
{
    int l=sta,r=n-1;
    int maxn,minn;
    int ans=-1;
    while(l<=r)
    {
        int mid=(l+r)/2;
        maxn=gma(sta,mid);
        minn=gmi(sta,mid);

        if(maxn>minn)
        {
            r=mid-1;
        }
        else if(maxn<minn)
        {
            l=mid+1;
        }
        else if(maxn==minn)
        {
            l=mid+1;
            ans=mid;
        }
    }
    return ans;
}

int main()
{
    while(~scanf("%d",&n))
    {
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        for(int i=0;i<n;i++)
            scanf("%d",&b[i]);

        cal();

        long long ans=0;
        for(int i=0;i<n;i++)
        {
            int s=bins(i);
            int e=bine(i);

            //printf("%d : %d %d\n",i,s,e);
            if(s!=-1 && e!=-1)
            {
                ans+=(e-s+1);
            }
        }
        printf("%lld\n",ans);
    }

}