斐波那契生兔子问题（一月大兔子生a对，二月大兔子生b对，三月大兔子生c对。。。）

        现提出一个问题：一对兔子一个月大时可生育a对兔子，两个月大的兔子生育b对兔子，三个月大及以后的兔子生c对兔子。假设兔子不死，现有1对兔子，问N个月后有多少只兔子。

        看起来这是一个递推数列的问题，要注意的地方在于，第n+1个月和第n个月的关系是，f(n+1)=第n个月的一月生兔子*a+第n个月的二月生兔子*b+第n个月的三月生及以后兔子*c。试图直接找递推关系将是很困难的。不妨用循环或者递归用状态转移的思想，从第一个月顺着推到n个月。

        兔子群里随时都是三种兔子，一月生二月生和三月生，所以我们要做的就是从头开始，每进行一个月算出下一个月的三种兔子分别是多少，然后让月份+1，当月份达到要求时推出即可。

        现令N=11，a=0,b=1,c=1（在这种情况下恰好构成斐波那契数列）

        递归版：

#include <iostream>
#include <cstdio>
using namespace std;

int total = 0,N=11;
int a=0,b=1,c=1;
void tuzi(int month,int first,int second,int third)
{
	if(month>N)
	{
		total = first + second + third;
		return ;
	}
	int f=first,s=second,t=third;
	f = first * a + second * b + third * c;
	s = first;
	t += second;
	tuzi(month+1,f,s,t);
}
int main()
{
	tuzi(1,1,0,0);
	cout<<total<<endl;
}

非递归版：

#include <iostream>
#include <cstdio>
using namespace std;
int a=0,b=1,c=1;
int main()
{
	int n=0;
	int f,first=1,s,second=0,t,third=0;
	while(n<11)
	{
		f=first;
		s=second;
		t=third;
		first = f*a+s*b+t*c;
		second = f;
		third += s;
		n++;
	}
	cout<<first+second+third<<endl;
}

当我们计算前11个月每月总数时，我们发现

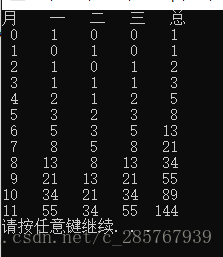
        结果刚好是我们熟悉的斐波那契数列f(n)=f(n-1)+f(n-2)。

        刚开始看到这道编程题的时候我也想过会不会第n个月和前面的有某种递推关系，但是没多想直接用DP的思想做了，做完了再会过来看才发现刚好是斐波那契数列。现在我们来看看为什么是这样。

        我们用f(n),s(n),t(n),g(n)分别代表第n个月时的一月生，二月生，三月(fst是first,second,third的意思)及以后的兔子数量，和g(n)总数。

        即有g(n)=f(n)+s(n)+t(n)。

        在上图结果中，我们随便找三行，可以发现以下关系：

                                                    t(n)=s(n-1)+t(n-1)，s(n)=f(n-1)，f(n)=s(n-1)+t(n-1)。

        然后再看s(n-1)和t(n-1)：    s(n-1)=f(n-2)，t(n-1)=s(n-2)+t(n-2)。

        带入上面f(n)中可得            f(n)=f(n-2)+s(n-2)+t(n-2)。

        最终可得                            g(n)=s(n-1)+t(n-1)+f(n-1)+f(n-2)+s(n-2)+t(n-2)，即g(n)=g(n-1)+g(n-2)