BFGS-MLM算法在机器人动力学辨识中的应用

工业机器人动力学参数辨识中BFGS‐MLM算法的研究

摘要

针对机器人动力学参数辨识问题，提出一种参数辨识算法。首先，采用非线性的Daemi‐Heimann经验摩擦模型描述关节间的摩擦特性，并建立动力学辨识模型。其次，为克服收敛速度慢的问题，在NMLM（新型改进 Levenberg‐Marquardt）算法基础上提出了用于参数辨识过程的BFGS‐MLM（改进Levenberg‐Marquardt）算法。该方法将非线性动力学参数辨识问题转化为非线性最小二乘问题，通过迭代求解最优值得到待辨识参数。在辨识过程中，采用线搜索策略求解BFGS‐MLM算法的最优迭代步长；结合 BFGS（Broyden, Fletcher, Goldfarb和Shanno）校正公式的拟牛顿法求解LM（Levenberg‐Marquardt）步长的近似Hessian逆矩阵，使算法具有更高的收敛速度。最后通过实验验证了该参数辨识方法的可行性。所提出的 BFGS‐MLM算法能有效提高动力学模型的辨识精度和迭代收敛速度，可为更复杂的非线性动力学参数辨识问题提供一种新的解决方案。

关键词 —机器人，动力学，参数辨识

I. 引言

准确的机器人动力学模型对于基于模型的控制、仿真分析和运动规划研究至关重要。然而，精确建立实际的机器人动力学模型较为困难。目前，通过参数辨识获取所需参数已成为建立机器人动力学模型的常用方法。

机器人参数辨识的常用方法主要有最小二乘法 [1‐2], 、最大似然估计法 [3] 和群智能算法 [4‐6]。由于受非线性因素的影响，学者们建立了具有非线性结构的关节摩擦模型，并采用群智能算法实现参数辨识。然而，仍存在收敛速度慢、辨识结果不一致等不足之处。

本文提出了一种改进的Levenberg‐Marquardt算法——BFGS‐MLM算法用于参数辨识。实验结果表明，该方法能够以更快的收敛速度实现非线性动力学参数辨识。

II. 机器人动力学辨识模型

A. 动力学模型

为了简化机器人动力学辨识模型并确保其准确性，我们仅建立机器人自身的动力学模型和关节摩擦模型。

根据机器人动力学理论，可采用牛顿‐欧拉法将具有 n 个关节的机器人的理想动力学模型转换为以下形式：

$$
\tau_{Ideal} = M(\theta)\ddot{\theta} + C(\theta,\dot{\theta})\dot{\theta} + G(\theta)
$$

如(1)所示，$\theta \in \mathbb{R}^n$ 是关节角向量，$M(\theta) \in \mathbb{R}^{n \times n}$是惯性项，$C(\theta,\dot{\theta}) \in \mathbb{R}^{n \times n}$是离心力且科里奥利力项， $G(\theta) \in \mathbb{R}^n$是重力项，$\tau_{Ideal} \in \mathbb{R}^n$ 表示理想条件下机器人关节的驱动力矩。

方程(1)可以进一步简化如下：

$$
\tau_{Ideal} = \Phi(\theta, \dot{\theta}, \ddot{\theta}) P
$$

如(2)所示，$\Phi(\theta, \dot{\theta}, \ddot{\theta}) \in \mathbb{R}^{n \times 10}$是仅与各关节运动参数相关的线性化矩阵。$P = [p_1^T, p_2^T, \dots, p_n^T]^T \in \mathbb{R}^{10n}$ 为n个关节中待识别参数的集合。

$$
p_i = [I_{xxi}, I_{xyi}, I_{xzi}, I_{yyi}, I_{yzi}, I_{zzi}, m_i r_{xi}, m_i r_{yi}, m_i r_{zi}, m_i]
$$

在上述方程中，Ixxi、 Ixyi、 Ixzi、 Iyyi、 Iyzi和 Izzi为连杆i的惯性张量项。$m_i r_{xi}$、$m_i r_{yi}$ 和 $m_i r_{zi}$ 表示一阶质量矩。mi是连杆 i 的质量。

参数集P中的冗余参数需要进一步处理。川崎 [7]和 霍伟 [8]使用惯性参数重组方法对(2)进行了简化。

$$
\tau_{Ideal} = \Phi’(\theta, \dot{\theta}, \ddot{\theta}) P_{min}
$$

如(4)所示，$\Phi’(\theta, \dot{\theta}, \ddot{\theta})$，是相应的回归重组后的矩阵，Pmin是重组后的最小惯性参数集。

B. 关节摩擦模型

相关研究表明，机器人关节驱动力矩中约有25%用于抵消由关节摩擦引起的摩擦力矩[9]。因此，精确的关节摩擦模型非常重要。为了简化摩擦特性的影响，采用线性形式的“库仑‐黏滞摩擦模型”来近似描述关节i的摩擦特性。

$$
\tau_{f,i} = f_{ci} \text{sgn}(\dot{\theta} i) + f {vi} \dot{\theta}_i
$$

如(5)式所示，f ci为关节i的库仑摩擦系数， f vi为关节i的黏滞摩擦系数。本文采用误差较小的Daemi‐Heimann经验摩擦模型来描述关节间的摩擦特性。

$$
\tau_{f,i} = f_{0i} + f_{ci} \text{sgn}(\dot{\theta} i) + f {vi} \dot{\theta} i + f {1i} \arctan(f_{2i} \dot{\theta}_i)
$$

如(6)所示，f 0i用于描述关节摩擦特性正反方向的差异。f 1i和 f 2i是描述关节摩擦特性的常数。该模型是由 Daemi [10]总结的经验模型。

结合(2)和(6)可得机器人动力学辨识模型为：

$$
\tau = \Phi’(\theta, \dot{\theta}, \ddot{\theta}) P_{min} + \tau_f
$$

如式(7)所示， $\tau_f = [\tau_{f,1}, \tau_{f,2}, \dots, \tau_{f,n}]^T \in \mathbb{R}^n$表示关节摩擦项。

III. 基于BFGS‐MLM算法的参数辨识方法

A. BFGS-MLM算法

采用群智能算法建立具有非线性形式的辨识模型，但存在辨识速度慢、辨识结果一致性差的问题。因此，本文提出一种基于改进的LM算法的参数辨识方法。

LM算法是Levenberg‐Marquardt算法的简称。它是一种广泛使用的非线性最小二乘数值解方法，具有收敛速度快、收敛结果一致性好的优点。对于标准LM算法，非线性最小二乘问题描述为：

$$
\min_{x \in \mathbb{R}} \frac{1}{2} f(x) = \frac{1}{2} |F(x)|^2
$$

首先，利用动态调整参数 μk 计算迭代方向向量。

$$
d_k = - (J_k^T J_k + \mu_k I)^{-1} J_k^T F_k
$$

如(9)所示，Jk是目标函数Fk的雅可比矩阵，I是单位矩阵。

其次，沿该向量计算新的迭代点。

$$
x_{k+1} = x_k + d_k
$$

标准LM算法在每次迭代计算过程中需要求解雅可比矩阵Jk以及近似海塞矩阵 $(J_k^T J_k + \mu_k I)$的逆矩阵，降低了算法的计算效率。Fan [11]和Yang [12]受两步牛顿法启发，提出了一种改进的MLM算法。

$$
y_k = x_k + d_k
$$

$$
d_k^{MLK} = - (J_k^T J_k + \mu_k I)^{-1} J_k^T F(y_k)
$$

$$
s_k = x_k + d_k^{MLK}
$$

$$
d_k^{HMLK} = - (J_k^T J_k + \mu_k I)^{-1} J_k^T F(s_k)
$$

$$
x_{k+1} = x_k + d_k + d_k^{MLK} + d_k^{HMLK}
$$

最后，基于改进的算法计算LM步长dk和近似的LM步长MLK kd及 HMLK kd ，得到新的迭代点。Chen [13]提出了一种改进的NMLM算法，用于求解每一步的最优步长。

$$
x_{k+1} = x_k + \lambda_k d_k + \lambda_k^{MLM} d_k^{MLM} + \lambda_k^{HMLM} d_k^{HMLM}
$$

如(16)所示， $\lambda_k^{MLM}$和 $\lambda_k^{HMLM}$是最优步长对应的系数。

上述NMLM算法无法有效提升算法的收敛能力。因此，本文提出了一种采用拟牛顿法的BFGS‐MLM算法，以进一步提高算法的收敛速度。

根据拟牛顿法，首先引入BFGS校正公式来求解近似海塞矩阵的逆矩阵。

$$
H_{k+1}^{MLM} = \left(I - \frac{d_k^{MLM} \Delta g_k^T}{d_k^{MLM T} \Delta g_k}\right) H_k \left(I - \frac{\Delta g_k d_k^{MLM T}}{d_k^{MLM T} \Delta g_k}\right) + \frac{d_k^{MLM} d_k^{MLM T}}{d_k^{MLM T} \Delta g_k}
$$

$$
\Delta g_k = J_k^T (F(y_k) - F(x_k))
$$

$$
H_k = (J_k^T J_k + \mu_k I)^{-1}
$$

使用近似的Hessian逆矩阵$H_k^{MLM}$求解 $d_k^{MLK}$，$H_k^{HMLM}$和 $d_k^{HMLK}$。

$$
d_k^{MLK} = - H_k^{MLM} J_k^T F(y_k)
$$

$$
H_k^{HMLM} = \left(I - \frac{d_k^{HMLM} \Delta g_k^T}{d_k^{HMLM T} \Delta g_k}\right) H_k^{MLM} \left(I - \frac{\Delta g_k d_k^{HMLM T}}{d_k^{HMLM T} \Delta g_k}\right) + \frac{d_k^{HMLM} d_k^{HMLM T}}{d_k^{HMLM T} \Delta g_k}
$$

$$
\Delta g_k = J_k^T (F(z_k) - F(x_k))
$$

$$
d_k^{HMLK} = - H_k^{HMLM} J_k^T F(z_k)
$$

最后，计算新的迭代点。

$$
x_{k+1} = x_k + \lambda_k d_k + \lambda_k^{MLM} d_k^{MLM} + \lambda_k^{HMLM} d_k^{HMLM}
$$

如(24)所示， $\lambda_k$、 $\lambda_k^{MLM}$和 $\lambda_k^{HMLM}$是通过线搜索策略获得的相应最优步长系数。

综上所述，BFGS‐MLM算法的具体步骤如下。

步骤1 ： 初始化。确定初始条件，例如迭代的初始点 x0, 、最大迭代次数 K、放大因子 σ、参数 β 和允许误差 0 < ε ≤ 1 。

步骤2 ： 判断迭代终止条件是否满足。如果 k=K，则迭代结束并进入步骤7。否则，计算 $g_k(x) = J_k^T F_k$。如果 $|g_k(x)| ≤ ε$ ，则迭代结束并进入步骤7。

步骤3 ： 求解迭代方向向量。计算 $d_k = - (J_k^T J_k + \mu_k I)^{-1} J_k^T F_k$和$f(x_k + d_k)$。如果 $(f(x_k + d_k) < f(x_k) + \beta g_k^T d_k)$ ，令 $\mu_{k+1} = \mu_k / \sigma$ 并执行步骤4。否则，令 $\mu_k = \mu_k \sigma$ 并重新运行步骤3。

步骤4 ： 求解近似的 LM 步 $d_k^{MLM}$ 。使用线搜索策略获得 λk，并从$y_k = x_k + \lambda_k d_k$ 获得 ky 。最后根据 (17) ~(20) 获得 $d_k^{MLM}$。

步骤5 ： 求解近似的 LM 步 $d_k^{HMLM}$，与步骤4相同。

步骤6 ： 更新迭代点 $x_{k+1}$。令 k=k+1 并计算 $x_{k+1} = x_k + \lambda_k d_k + \lambda_k^{MLM} d_k^{MLM} + \lambda_k^{HMLM} d_k^{HMLM}$。然后执行步骤2。

步骤7 ： 迭代结束后，输出最终的迭代结果 $x_k$。

B. 参数识别算法

本文提出了一种改进的摩擦模型，该模型使用反正切函数作为库仑摩擦项的近似。

$$
\tau_{f,i} = f_{0i} + f_{ci} \frac{2}{\pi} \arctan(\rho \dot{\theta} i) + f {vi} \dot{\theta} i + f {1i} \arctan(f_{2i} \dot{\theta}_i)
$$

如(25)所示，ρ是用于调整近似正切函数对符号函数误差的修正系数。本文中，ρ=10000。

使用每个关节数据采集点的预测力矩与测量力矩之间的差值作为目标函数。

$$
F(x) = \sum_{i=1}^{n} \sum_{j=1}^{N} (\tau_{ij,predict} - \tau_{ij,measure})
$$

如式(26)所示，n为机器人关节数量，N为单个关节采集的数据长度。将上述方程代入式(8)，可将参数辨识问题转化为非线性最小二乘问题，通过求解使式(8)最小的x来获得结果。

IV. 工业机器人参数辨识实验

为了验证上述BFGS‐MLM算法的参数辨识性能，设计了相关实验进行验证。首先，根据6自由度工业机器人设计激励轨迹。其次，按照设计轨迹采集机器人运动过程中各关节的运动数据和关节力矩数据。最后，将数据代入参数识别算法中，对机器人动力学参数进行辨识。

A. 激励轨迹设计

图1所示的川崎RS010N机器人作为实验研究对象。我们研究该机器人在空载条件下前三个关节的动力学参数辨识。

Swevers [14]使用遗传算法优化激励轨迹的数学模型，用于求解以 $\theta_{i0}$、 $a_{il}$和$b_{il}$为优化变量的非线性约束优化问题。

$$
\theta_i(t) = \theta_{i0} + \sum_{l=1}^{M} (a_{il} \sin(\omega_l t) + b_{il} \cos(\omega_l t)), \quad \omega_l = \frac{l \omega_f}{M}
$$

如(27)所示， $\theta_{i0}$为常数， $a_{il}$和$b_{il}$为三角函数的幅值常数。M为轨迹的谐波数量。本文中，M=5且 $\omega_f$为基频。

式(28)表示轨迹约束。T为运动的结束时间。

$$
\begin{cases}
\theta_i^{min} \leq \theta_i(t) \leq \theta_i^{max} \
\theta_i(0) = \theta_i(T) \
\dot{\theta}_i^{min} \leq \dot{\theta}_i(t) \leq \dot{\theta}_i^{max} \
\dot{\theta}_i(0) = \dot{\theta}_i(T) \
\ddot{\theta}_i^{min} \leq \ddot{\theta}_i(t) \leq \ddot{\theta}_i^{max} \
\ddot{\theta}_i(0) = \ddot{\theta}_i(T)
\end{cases}
$$

$$
\begin{cases}
\Phi^{min} \leq \Phi(\theta, \dot{\theta}, \ddot{\theta}) \leq \Phi^{max} \
\theta_i(0) = \theta_i(T) \
\dot{\theta}_i(0) = \dot{\theta}_i(T) \
\ddot{\theta}_i(0) = \ddot{\theta}_i(T)
\end{cases}
$$

本文中，辨识模型的回归矩阵条件的最小数量是优化指标函数[15]。

B. 动力学参数辨识实验

根据上一节设计的机器人激励轨迹，我们可以获得关节运动结果。

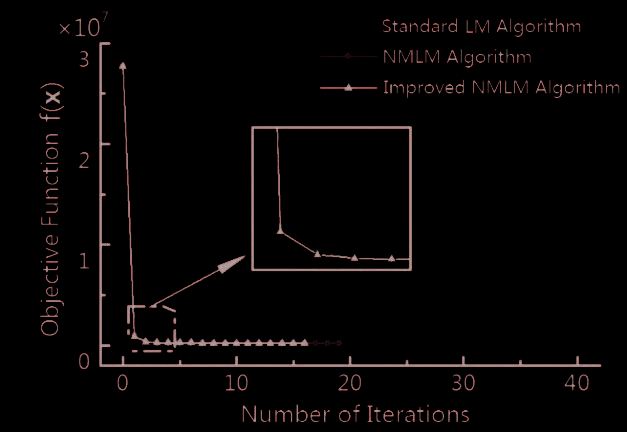
取初始值 $x_0 = [1, 1, 1, \dots]^T$ ， $\sigma = 10$ ， $\beta = 0.55$ ，$\mu_k = 0.01$，并采用黄金分割法作为线搜索策略。与标准LM算法、NMLM算法和BFGS‐MLM算法相比，辨识的迭代过程如图3所示。

从图中可以看出，在相同的迭代过程中，NMLM算法和BFGS‐MLM算法计算得到的目标函数值明显小于标准LM算法计算得到的目标函数值。

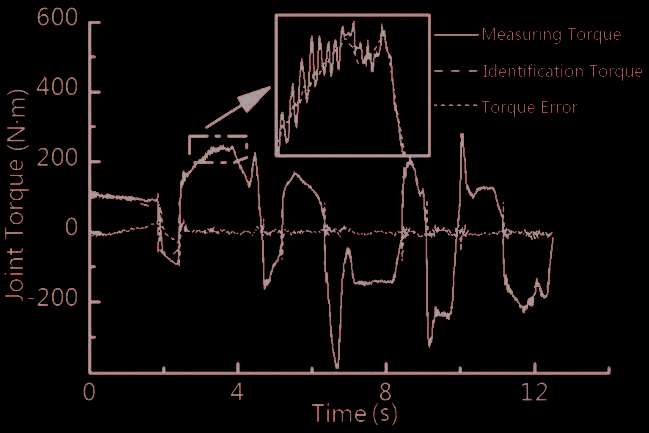
从图中可以看出，辨识出的力矩与测量力矩高度一致，表明BFGS‐MLM算法是可行的。

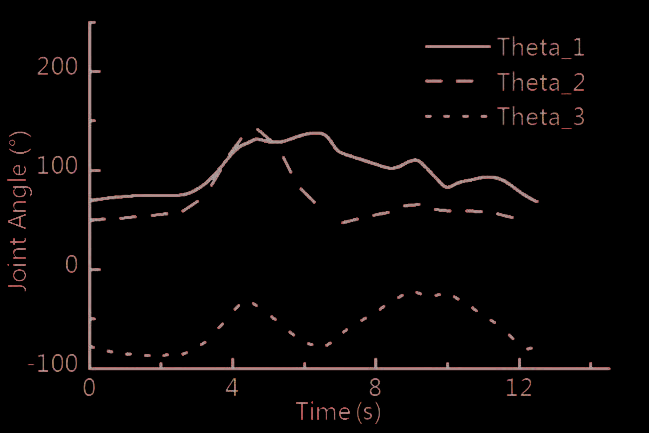
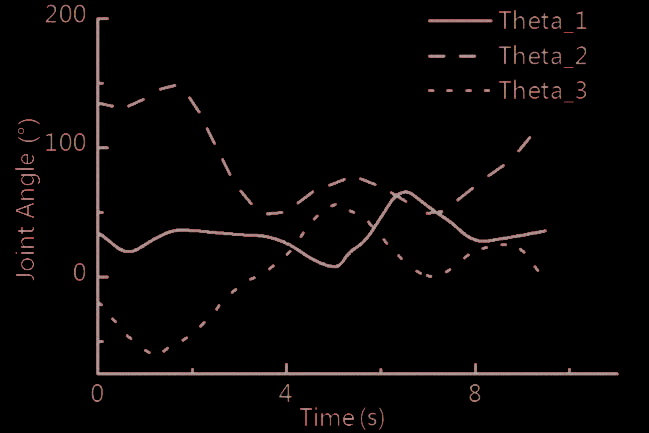
设计另一条验证轨迹以描述机器人在随机轨迹下的动力学特性。验证轨迹中各关节运动曲线如图5所示。

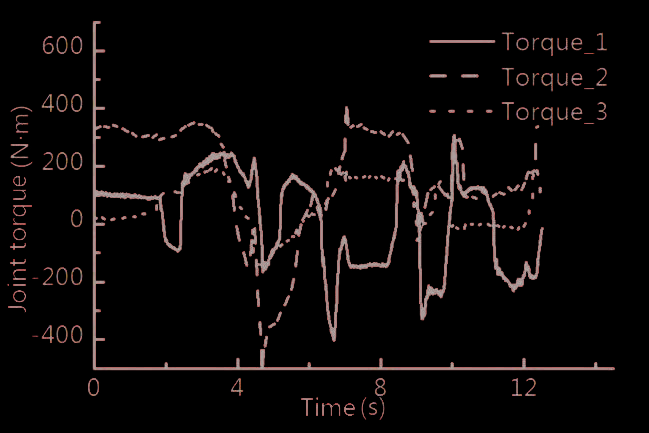
将验证轨迹的运动参数代入已辨识的动力学模型中，关节驱动力矩对比结果如图6所示。

)

从图6可以看出，BFGS‐MLM算法能够有效解决非线性动力学模型的参数辨识问题。

五、结论

针对具有非线性结构的机器人动力学辨识问题，本文提出了一种基于BFGS‐MLM算法的参数辨识方法。对动力学的摩擦模型进行了修正，以保证模型的连续可微性。此外，为了提高收敛速度，采用了拟牛顿法和线搜索策略来寻找最优迭代步长。BFGS‐MLM算法能够提高动力学模型的收敛速度和辨识精度，从而有效解决机器人非线性动力学模型的参数辨识问题，同时也为其他更复杂的非线性动力学参数辨识问题提供了新的解决方案。