多采样率信号处理 ——信号的抽取与插值 学习笔记

信号的抽取与插值基本处理流程如下图（图片来源https://blog.youkuaiyun.com/shenziheng1/article/details/53373807?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522170126176516800222875499%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=170126176516800222875499&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allsobaiduend~default-1-53373807-null-null.142^v96pc_search_result_base2&utm_term=%E6%8A%BD%E5%8F%96%20%E6%8F%92%E5%80%BC&spm=1018.2226.3001.4187）

抽取与插值是一个对偶的概念，所以处理的方式也是相互对偶的。

1. 抽取

   当信号的抽样数据量太大时，为了减少数据量以便于处理和计算，我们把抽样数据每隔(D-1)个取一个，这里 D 是一个整数。这样的抽取称为整数倍抽取，D 称为抽取因子。通常用符号“D”表示将抽样率降为原来的 1/D，其中D为 Decimation 的第一个字母。
   
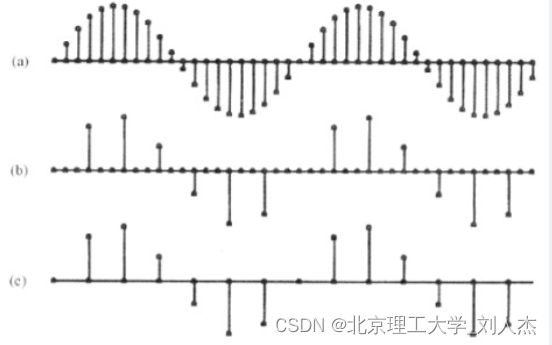
   那么抽取之后，频域图会发生什么变化呢？

   假设某一个系统中，模拟信号只在0~2 kHz 的频段内有信号，利用6kHz 的频率进行 A/D采样，则采样后的信号没有频谱混叠，频谱周期为6kHz，信号的频谱图如图(a)所示。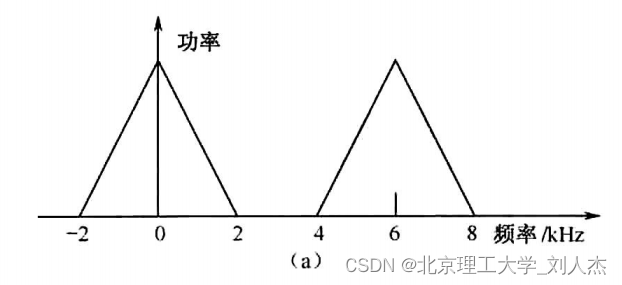![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/99e197ec25ba49e78ed896166010e36a.png)
   

   如果直接对 6kHz 的信号进行 2 倍抽取，则抽取后的信号频谱周期降为 3 kHz，频谱形状没有发生改变，但周期缩短了，导致信号频谱出现了混叠，如图 (b)所示。混叠的原因还可以从采样定理的角度来理解，抽取后的信号采样频率为 3 kHz，而原模拟信号的最高频率为 2kHz，显然不满足无混叠抽样条件，出现频率混叠也就理所当然了。
   
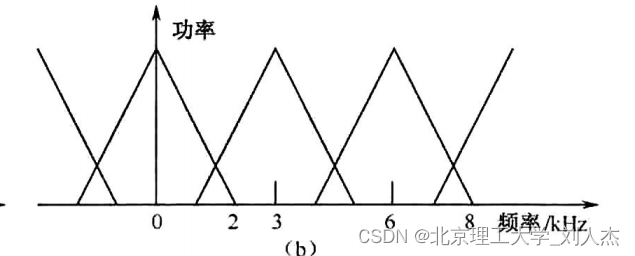
   因此，只有在抽取之后的抽样率仍然符合抽样定理的要求时，才能无失真地恢复出原来的模拟信号，否则就必须采取措施。通常采取的措施是抗混叠滤波。所谓抗混叠滤波，就是在抽取之前，对信号进行低通滤波，把信号的频带限制在抽样后频率的一半以下，这样，整数倍抽取的问题其实变成了一个低通滤波的问题。
   也就是说，你想要的信号在抽取之前归一化的角频率要小于0.5π！！
   而为了防止抽取的时候高频混叠，一般通常需要进行低通滤波（半带滤波器或CIC滤波器是常用的选择）。所以抽取的过程是先滤波后抽取（时刻记住对偶，所以插值是先补零后滤波）。
   如果有多次抽取，可以想到，随着采样频率的下降，滤波器的过渡带越来越窄，而滤波器的阶数会越来越高（这个也是对偶的，插值滤波器的话就是滤波器阶数越来越低）
   比如用3级半带滤波器进行抽取，

   插值就是补零。

close all
fs = 200;
f1 = 10;
n = 4096;
t = 0:1/fs:(n-1)/fs;
x_in = cos(2*pi*f1*t) ;

figure
subplot(211)
plot(x_in(1:500))
title("时域图")
subplot(212)
pwelch(x_in)
title("频域图")

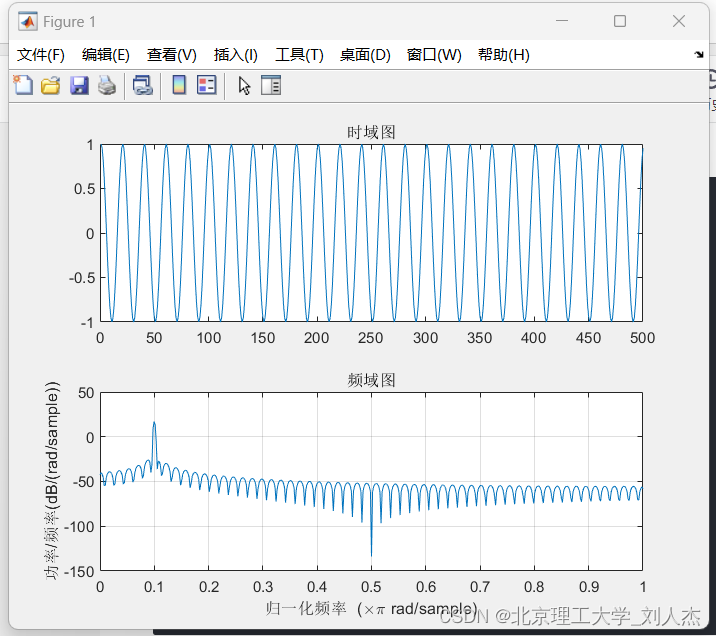
由于此时只需要保证归一化频率中0-0.1这一段低通信号完整，而其他的频段都可以看做是噪声，故可以利用MATLAB filterDesigner设计半带低通滤波器