剑指offer(三） --矩阵旋转

最新推荐文章于 2025-06-03 12:13:40 发布

原创最新推荐文章于 2025-06-03 12:13:40 发布 · 495 阅读

0 ·

CC 4.0 BY-SA版权

python 同时被 2 个专栏收录

28 篇文章

订阅专栏

剑指offer

7 篇文章

订阅专栏

本文详细介绍了如何使用Python的map和zip函数实现矩阵的顺时针和逆时针旋转，以及矩阵转置的方法。通过示例代码解析了矩阵旋转的逻辑过程，并探讨了zip函数在矩阵转置中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

class Solution:
    # matrix类型为二维列表，需要返回列表
    def printMatrix(self, matrix):
        # write code here
        mSize=len(matrix)
        xSize=len(matrix[0])
        listR=[]
        listR.extend(matrix[0])

        for i in range(mSize*xSize):
            if len(listR)<mSize*xSize:
                matrix.__delitem__(0)
                self.rotate(matrix)
                listR.extend(matrix[0])
            else:
                break
        return listR


    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        #matrix[:] = map(list,zip(*matrix[::-1]))  #顺时针旋转
        matrix[:] = map(list, zip(*matrix))[::-1]  #逆时针旋转
        #return matrix

参考网址：

旋转矩阵：https://blog.youkuaiyun.com/shawpan/article/details/69663710

map和zip函数讲解：https://blog.youkuaiyun.com/qq_42169668/article/details/80253229

二. map和zip函数与旋转

首先Python中的map函数是很简单的。意为将第二个参数（一般是数组）中的每一个项，处理为第一个参数的类型。比如如下的代码，将a这个list的每一项都从int类型转化为str类型。

    #-*-coding:utf-8-*-  
    a=[1,2,3];  
    print map(str,a);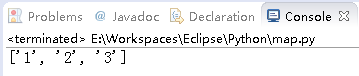

而如下的数组，则对a这个二维数组中的每一个项的一维数组进行求和操作，最后得出来自然是一个一维数组，因为每一个项的一维数组，转化为一个int。

#-*-coding:utf-8-*-
a=[[1,3,4],[2,3,2]];
print map(sum,a);

运行结果如下：

二、zip(*)

在《【Python】用zip函数求欧氏距离、余弦相似度》（点击打开链接）中已经介绍了zip的使用，

zip(...)
zip(seq1 [, seq2 [...]]) -> [(seq1[0], seq2[0] ...), (...)]
Return a list of tuples, where each tuple contains the i-th element
from each of the argument sequences. The returned list is truncated
in length to the length of the shortest argument sequence.

比如下述的一段代码：

[python] view plain copy

#-*-coding:utf-8-*-
x=[1,2,3];
y=[4,5,6];
z=[7,8,9];
print zip(x,y,z);

运行结果如下：

意思是取各个list的第x项，作为返回的二维数组的第x项中的一维数组中的元素。

其实zip还是反过来会这个二维数组操作，但要注意写成zip(*)，表示这是一个zip的逆操作。

比如下述的一段代码：

[python] view plain copy

# -*-coding:utf-8-*-
array=[[1,4,7],[2,5,8],[3,6,9]];
x,y,z=zip(*array);
print x,y,z;

xyz的值分别如下所示，恰好与zip函数形成一个逆操作。

矩阵旋转：（python里存储矩阵，一般以list里的list存储）

#matrix[:] = map(list,zip(*matrix[::-1])) #顺时针旋转

所以具体的过程就是，比如[[1,2,3],[4,5,6]]

matrix[:,:,-1]后，就是[ [4,5,6],[1,2,3] ]

然后，zip(*matrix[::-1]) 就是一列一列的取，并转化为元组tuple,即（4,1），（5,2），（6,3）

再map转化为list类型，[[4,1],[5,2],[6,3]]

这就完成了顺时针旋转

matrix[:] = map(list, zip(*matrix))[::-1] #逆时针旋转

逆时针旋转则是这样：

<1. zip函数，转换矩阵为（（1,4,），（2,5），（3,6））

<2.map函数,转换为【【1，4】，【2,5】，【3,6】】

<3. [::-1]反向为【【3,6】，【2,5】，【1,4】】,完毕

三.python矩阵的转置

这与数组转置有什么相关呢？

注意到，如果zip(*array)不经过x,y,z=zip(*array);拆分成x,y,z三个变量，那么[[1,4,7],[2,5,8],[3,6,9]];被zip(*array)之后的结果恰好是[(1, 2, 3), (4, 5, 6), (7, 8, 9)]，刚好形成一个转置的关系。这对于所有array=[[1,2,3],[4,5,6],[7,8,9]];的二维数组都是一样的，不信可以试试。

当然[(1, 2, 3), (4, 5, 6), (7, 8, 9)]还不是我们需要的最后的结果，

因为只是一个存放tuple的list，我们要保持原来list是存list的一致性，所以要应用到上方的map函数。

因此对于一个数组的转置，代码如下：

[python] view plain copy

# -*-coding:utf-8-*-
array = [[1, 4], [2, 5], [3, 6]];
print map(list, zip(*array));

运行结果如下：

封装成类的子函数：


    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        #matrix[:] = map(list,zip(*matrix[::-1]))  #顺时针旋转
        #matrix[:] = map(list, zip(*matrix))[::-1]  #逆时针旋转
        matrix[:]=map(list, zip(*array))  #矩阵转置 
        #return matrix

值得注意的是，在调用同一类的子函数时，需要前面加上self.